2n BATXILLERAT: MOVIMENT VIBRATORI HARMÒNIC SIMPLE.
- 2. MOVIMENT PERIÒDIC És aquell que descriu un cos quan les variables cinemàtiques: posició, velocitat i acceleració del seu moviment prenen els mateixos valors després de cada interval constant de temps anomenat: PERÍODE .
- 3. MOVIMENT VIBRATORI O OSCIL·LATORI És aquell que descriu un cos quan es desplaça succesivament a una banda i l’altra de la seva posició d’equilibri repetint a intervals regulars de temps les seves variables cinemàtiques.
- 4. APLICACIONS DE L’ESTUDI DEL MVHS ENLLAÇ QUÍMIC VIBRACIONS EDIFICIS VIBRACIONS PONTS
- 5. VOCABULARI VIBRACIÓ O OSCIL·LACIÓ: distància recorreguda per una partícula en un moviment complet de vaivén. CENTRE D’OSCIL·LACIÓ (O): punt mitjà de la distància que separa les dues posicions extremes assolides per la partícula mòbil. ELONGACIÓ (x): distància de la partícula al centre d’oscil·lació en cada moment. (unitat: m)
- 6. AMPLITUD (A): Valor màxim de la elongació. (unitat: m) PERÍODE (T): temps emprat per la partícula en efectuar una oscil·lació completa. (unitat: s) FREQÜÈNCIA (f): nombre d’oscil·lacions efectuades en la unitat de temps. (unitat: Hz) (f = 1/T) PULSACIÓ (ω): nombre de períodes compresos en 2π unitats de temps. ω = 2πf = 2π/T (unitat: rad/s)
- 7. MVHS Un moviment oscil·latori sobre una trajectòria recta és harmònic simple si està sotmés a una força d’atracció proporcional al vector de posició, amb origen en el seu punt d’equilibri i de sentit contrari: força recuperadora . F = m a F = - K x i Una partícula té un moviment MHS al llarg d’un eix X quan la seva elongació s’expressa mitjançant una funció sinusoïdal o cosenoïdal.
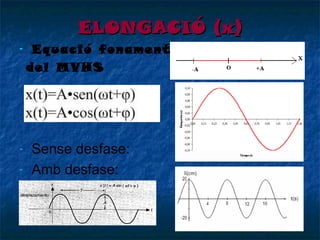
- 8. ELONGACIÓ (x) - - Equació fonamental del MVHS Sense desfase: Amb desfase:
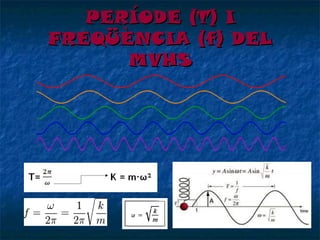
- 9. PERÍODE (T) I FREQÜÈNCIA (f) DEL MVHS
- 10. VELOCITAT (v) Si prové d’una equació sinusoïdal: Si prové d’una equació cosinoïdal:
- 11. ACCELERACIÓ (a) Si prové d’una equació sinusoïdal: Si prové d’una equació cosinoïdal:
- 12. RELACIÓ: x – v - a
- 13. GRÀFICS: x – v - a Sense desfase Amb desfase
- 14. Per a una elongació cosinoïdal:
- 16. DINÀMICA DE L’OSCILADOR HARMÒNIC SIMPLE. Força recuperadora:
- 17. ENERGIA DE L’OSCILADOR HARMÒNIC SIMPLE ENERGIA TOTAL ENERGIA POTENCIAL ENERGIA CINÈTICA
- 18. RESUMEN FÓRMULES AMB EL SINUS
- 19. PÈNDOL SIMPLE El moviment del pèndol simple és un moviment harmònic simple sempre que es considerin desplaçaments molt petits. Veure MIT
- 20. PÈNDOL DE FOUCAULT Comprovació de la rotació de la Terra. La corda ha de ser molt llarga.
- 21. ALTRES MOVIMENTS VIBRATORIS Oscil·lacions amortides. Oscil·lacions forçades. Ressonància.
- 22. OSCIL·LACIONS AMORTIDES L’amplitud de les oscil·lacions va disminuint amb el temps degut a la pèrdua d’energia mecànica, sobre tot per causa del fregament.
- 23. OSCIL·LACIONS FORÇADES Són produïdes en un sistema oscil·latori a causa de l’energia subministrada des de l’exterior; aquest sistema és un oscil·lador forçat .
- 24. RESSONÀNCIA Un osci·lador entra en ressonància quan la freqüència d’una força externa coincideix amb la freqüència natural de l’oscil·lador. Exemples: Pont de Tacoma Els soldats no poden travessar ponts amb marxa militar.
- 25. Copa trencada Insectes amb ales:
- 26. FIGURES DE LISSAJOUS Si sobre una partícula actuen dues forces en direcció perpendicular i de mateix període que originen un MVHS, el moviment resultant té trajectòria el·líptica. Fes CLICK
- 27. ENLLAÇ A ALTRA PRESENTACIÓ D’AQUEST MOVIMENT.
- 28. Rosa Mª Rodríguez García-Caro Professora de física i química IES ALCÚDIA ALCÚDIA (MALLORCA)