�ݺ�ߣ

Pythagorean Triples
The student is able to (I can):
? Learn to identify and use Pythagorean triples
? Review how to simplify radicals

Square Roots
? When we are taking the square root of a number, we will
not always get a whole number answer.
? If your answer is not a whole number, then the number
your calculator gives you is a decimal approximation. This
is an irrational number, like ?, which goes on forever.
? If I ask for an exact answer, I do not want a decimal �C I
want you to leave it as a simplified radical.

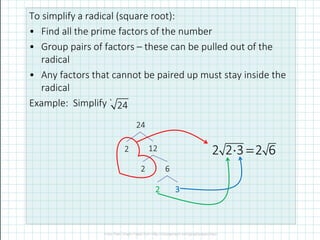
To simplify a radical (square root):
? Find all the prime factors of the number
? Group pairs of factors �C these can be pulled out of the
radical
? Any factors that cannot be paired up must stay inside the
radical
Example: Simplify ` 24
24
2 12
2 6
2 3
? =
2 2 3 2 6

Radicals with variables are actually much easier to simplify.
? For each variable, divide the variable��s exponent by the
index of the radical (square roots have index 2, cube roots
have index 3, etc.).
? If the division results in an improper fraction, the whole
part goes on the outside and the remainder stays inside.
(This is one of the few instances where I actually prefer
mixed numbers.)
Example: Simplify 5
8y
8
2
2
4
2
y5
1
5 2 2
2
? = 2 1
2 2
y y

Examples
Find the value of x. Reduce radicals to simplest form.
1.
2.
2
6
x
x x-2
4

Examples
1.
2.
2 2 2
2 6 x
+ =
2
4 36 x
+ =
2
40 x
=
2 10
x =
2
6
x
x x-2
4

Examples
1.
2.
2 2 2
2 6 x
+ =
2
4 36 x
+ =
2
40 x
=
2 10
x =
2 2 2
4 ( 2)
x x
+ ? =
2
6
x
x x-2
4

Examples
1.
2.
2 2 2
2 6 x
+ =
2
4 36 x
+ =
2
40 x
=
2 10
x =
2 2 2
4 ( 2)
x x
+ ? =
x -2
x x2 -2x
-2 -2x 4
2 2
16 4 4
x x x
+ ? + =
2
6
x
x x-2
4

Examples
1.
2.
2 2 2
2 6 x
+ =
2
4 36 x
+ =
2
40 x
=
2 10
x =
2 2 2
4 ( 2)
x x
+ ? =
x -2
x x2 -2x
-2 -2x 4
2 2
16 4 4
x x x
+ ? + =
20 �C 4x = 0
20 = 4x
x = 5
2
6
x
x x-2
4

Pythagorean Triple
A set of nonzero whole numbers a, b, and c, such that
a2 + b2 = c2.
Memorize these!
While you don��t have to memorize these, it can make your
life easier if you can recognize them.
3, 4, 5 is the only triple that contains three
consecutive numbers.
Pythagorean Triples
Base 3, 4, 5 5, 12, 13 7, 24, 25 8, 15, 17
?2 6, 8, 10 10, 24, 26 14, 48, 50 16, 30, 34
?3 9, 12, 15
x4 12, 16, 20
x5 15, 20, 25

Examples
Find the missing side of the right triangle.
1. 3, 4, ____
2. 9, ____, 15
3. ____, 12, 13
4. 8, 15, ____

Examples
Find the missing side of the right triangle.
1. 3, 4, ____
2. 9, ____, 15 (multiple of 3-4-5)
3. ____, 12, 13
4. 8, 15, ____
5
12
5
17

�ݺ�ߣ

7.2 Pythagorean Triples and Simplifying Radicals

More Related Content

7.2 Pythagorean Triples and Simplifying Radicals