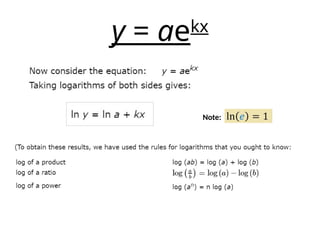�ݺ�ߣ

Paper 5: planning, analysis and
evaluation

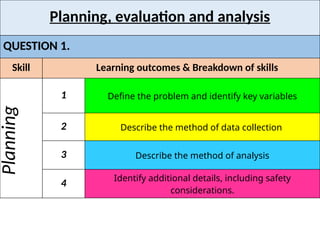
Planning, evaluation and analysis
QUESTION 1.
Skill Learning outcomes & Breakdown of skills
Planning
1 Define the problem and identify key variables
2 Describe the method of data collection
3 Describe the method of analysis
4 Identify additional details, including safety
considerations.

Defining the problem
• identify the independent variable in the experiment
• identify the dependent variable in the experiment
• identify the variables that are to be kept constant.

Methods of data collection
• describe the method to be used to vary the independent variable
• describe how the independent and dependent variables are to be
measured
• describe how other variables are to be kept constant

Cont.
• describe, with the aid of a clear labelled diagram, the
arrangement of apparatus for the experiment and the
procedures to be followed.

Method of analysis
• describe how the data should be used in order to reach a
conclusion, including details of derived quantities to be
calculated from graphs.

Additional detail including safety
considerations
• assess the risks of their experiment
• describe precautions that should be taken to keep risks to a
minimum.

Planning, analysis and evaluation
QUESTION 2.
ysis,
conclusion
and
evaluation
1 Analyse data and obtain constants from graphs and
rearrange equations in the form of y=mx+c
2 Complete a table of results.
3 Correctly plot a graph
4 Draw conclusions from the graph
5 Calculate and plot uncertainties

Data analysis
Candidates should be able to:
• rearrange expressions into the forms y = mx + c,
• understand how a graph of y against x is used to find the constants m and c
in an equation of the form y = mx + c
• decide what derived quantities to calculate from raw data in order to
enable an appropriate graph to be plotted.
Eg: to verify the relationship
a graph is plotted of on the y-axis and on the x-axis. Determine an expression for
the gradient (m). What should the y-intercept (c) value be according to the above equation.
m =
c =

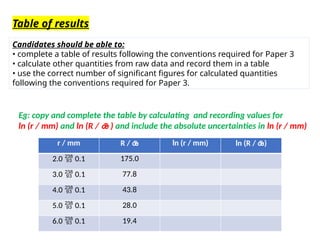
Table of results
• complete a table of results following the conventions required for Paper 3
• calculate other quantities from raw data and record them in a table
• use the correct number of significant figures for calculated quantities
following the conventions required for Paper 3.
r / mm R /  ln (r / mm) ln (R / )
2.0  0.1 175.0
3.0  0.1 77.8
4.0  0.1 43.8
5.0  0.1 28.0
6.0  0.1 19.4
Eg: copy and complete the table by calculating and recording values for
ln (r / mm) and ln (R /  ) and include the absolute uncertainties in ln (r / mm)

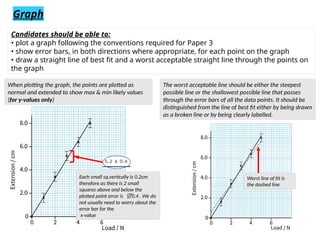
Graph
The worst acceptable line should be either the steepest
possible line or the shallowest possible line that passes
through the error bars of all the data points. It should be
distinguished from the line of best fit either by being drawn
as a broken line or by being clearly labelled.
When plotting the graph, the points are plotted as
normal and extended to show max & min likely values
(for y-values only)
Each small sq.vertically is 0.2cm
therefore as there is 2 small
squares above and below the
plotted point error is 0.4 . We do
not usually need to worry about the
error bar for the
x-value
Worst line of fit is
the dashed line
• plot a graph following the conventions required for Paper 3
• show error bars, in both directions where appropriate, for each point on the graph
• draw a straight line of best fit and a worst acceptable straight line through the points on
the graph

• determine the gradient and y-intercept of a straight-line graph
• derive expressions that equate to the gradient or the y-intercept of their straight lines
of best fit
• draw the required conclusions, with correct units and appropriate number of
significant figures, from these expressions.
Conclusio
n
Treatment of uncertainties
• convert absolute uncertainty estimates into fractional or percentage
uncertainty estimates and vice versa
• show uncertainty estimates, in absolute terms, beside every value in a table of
results
• calculate uncertainty estimates in derived quantities
• estimate the absolute uncertainty in the gradient of a graph by recalling that:
• estimate the absolute uncertainty in the y-intercept of a graph by recalling that
absolute uncertainty = y-intercept of line of best fit – y-intercept of worst
acceptable line
• express a quantity as a value, an uncertainty estimate and a unit.

8.-Planning--Analysis-and-evaluation.pptx

Lesson 3 : More
complicated analysis
of data

Planning, analysis and evaluation
QUESTION 2.
Analysis
1 rearrange expressions into the forms y = axn
and y = aekx
2
understand how a graph of log y against log x is used to
find the constants a and n in an equation of the form y =
axn
3 understand how a graph of ln y against x is used to find
the constants a and k in an equation of the form y = aekx
4
decide what derived quantities to calculate from raw
data in order to enable an appropriate graph to be
plotted

Extra: How do you find the antilog of a
number?
Log antilog
Where:
b= base (usually 10 or e)
X= log value
Y= number
Question1) Ln (x) = 0.4
x = e0.4
x = _________
Question 2) Lg (x) = 4
x = 104
x=___________

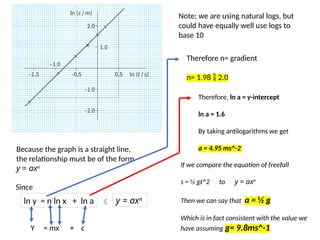
Because the graph is a curve it tells us little about
the relationship between the variables. If, However, we
suspect the relationship is of the form y = axn
, we can
test this idea by plotting ln s against ln t
A ball falls under gravity in the absence of air resistance. It falls a distance of s in time t. The results are
given in the first two columns below. A graph of distance fallen against time gives the curve shown below.
A relationship of the form

Note: we are using natural logs, but
could have equally well use logs to
base 10
Because the graph is a straight line,
the relationship must be of the form
y = axn
y = axn
Since
Therefore n= gradient
n= 1.98  2.0
Y = mx + c
ln y = n ln x + ln a 
Therefore, ln a = y-intercept
ln a = 1.6
By taking antilogarithms we get
a = 4.95 ms^-2
If we compare the equation of freefall
s = ½ gt^2 to y = axn
Then we can say that a = ½ g
Which is in fact consistent with the value we
have assuming g= 9.8ms^-1

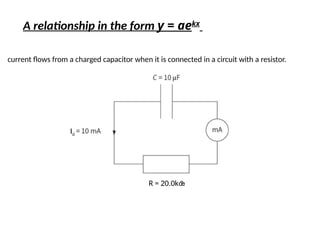
A relationship in the form y = aekx
current flows from a charged capacitor when it is connected in a circuit with a resistor.
Io
R = 20.0k

Time/s
The graph obtained shows a typical
decay curve, but we cannot be sure it is
exponential. To show the curve is of
the form I = Ioekt
We plot ln I against t

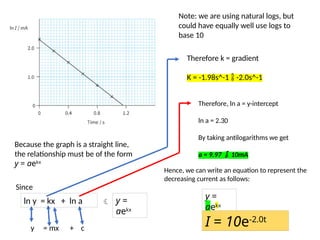
Note: we are using natural logs, but
could have equally well use logs to
base 10
Because the graph is a straight line,
the relationship must be of the form
y = aekx
y =
aekx
Since
Therefore k = gradient
K = -1.98s^-1  -2.0s^-1
y = mx + c
ln y = kx + ln a 
Therefore, ln a = y-intercept
ln a = 2.30
By taking antilogarithms we get
a = 9.97  10mA
Hence, we can write an equation to represent the
decreasing current as follows:
y =
aekx
I = 10e-2.0t

Question
Can you
a) …identify graph that you must plot?
b) …find a value for k ?
c) …find a value for s ?

�ݺ�ߣ

8.-Planning--Analysis-and-evaluation.pptx

Recommended

More Related Content

Similar to 8.-Planning--Analysis-and-evaluation.pptx (20)

More from SumayyaPA4 (12)

Recently uploaded (20)

8.-Planning--Analysis-and-evaluation.pptx

Editor's Notes