8.2 The Hyperbola
- 1. 8.2 The Hyperbola Chapter 8 Analytic Geometry
- 2. Concepts and Objectives âŦ The objectives for this section are âŦ Locate a hyperbolaâs vertices and foci. âŦ Write equations of hyperbolas in standard form. âŦ Graph hyperbolas centered at the origin. âŦ Graph hyperbolas not centered at the origin. âŦ Solve applied problems involving hyperbolas.
- 3. Hyperbolas âŦ Hyperbolas have two disconnected branches. Each branch approaches diagonal asymptotes. âŦ Parts of a hyperbola: âŦ Center âŦ Vertices âŦ Asymptotes âŦ Hyperbola âĒ âĒ âĒ
- 4. Hyperbolas âŦ The general equation of a hyperbola is or âŦ The hyperbola opens in whichever direction has the positive term (x-direction if x is positive, y-direction if y is positive). âŦ The slope of the asymptotes is always . âŦ The vertices are ïąrx or ïąry from the center, whichever term is positive. a is the positive term radius, b is the negative term radius. ïĶ ïķ ïĶ ïķ â â â = ï§ ï· ï§ ï· ï§ ï· ïĻ ïļ ïĻ ïļ 2 2 1 x y x h y k r r ïĶ ïķ ïĶ ïķ â â â + = ï§ ï· ï§ ï· ï§ ï· ïĻ ïļ ïĻ ïļ 2 2 1 x y x h y k r r ïą y x r r
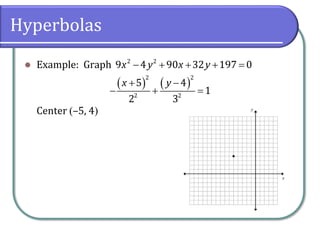
- 5. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y
- 6. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) ( ) ( ) + + â = + + â â â 2 2 2 2 2 2 9 10 8 197 5 9 5 4 4 4 4 x x y y Notice that the negative sign has been factored as well! Remember to distribute the negative sign!
- 7. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) ( ) ( ) + + â = + + â â â 2 2 2 2 2 2 9 10 8 197 5 9 5 4 4 4 4 x x y y ( ) ( ) + â â = â 2 2 9 6 4 4 5 3 x y Notice that the negative sign has been factored as well! Remember to distribute the negative sign!
- 8. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) ( ) ( ) + + â = + + â â â 2 2 2 2 2 2 9 10 8 197 5 9 5 4 4 4 4 x x y y ( ) ( ) + â â â = â â â 2 2 9 5 4 4 36 36 36 36 x y Notice that the negative sign has been factored as well! Remember to distribute the negative sign!
- 9. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) ( ) ( ) + + â = + + â â â 2 2 2 2 2 2 9 10 8 197 5 9 5 4 4 4 4 x x y y ( ) ( ) + â â â = â â â 2 2 9 5 4 4 36 36 36 36 x y ( ) ( ) + â â + = 2 2 5 4 1 4 9 x y Notice that the negative sign has been factored as well! Remember to distribute the negative sign!
- 10. Hyperbolas âŦ Example: Graph â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) ( ) ( ) + + â = + + â â â 2 2 2 2 2 2 9 10 8 197 5 9 5 4 4 4 4 x x y y ( ) ( ) + â â â = â â â 2 2 9 5 4 4 36 36 36 36 x y ( ) ( ) + â â + = 2 2 5 4 1 4 9 x y ( ) ( ) + â â + = 2 2 2 2 5 4 1 2 3 x y Notice that the negative sign has been factored as well! Remember to distribute the negative sign!
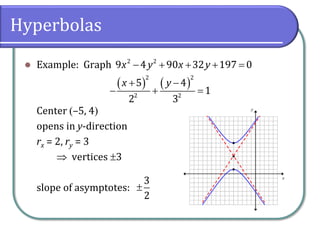
- 11. Hyperbolas âŦ Example: Graph Center (â5, 4) â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) + â â + = 2 2 2 2 5 4 1 2 3 x y
- 12. Hyperbolas âŦ Example: Graph Center (â5, 4) opens in y-direction rx = 2, ry = 3 ï vertices ïą3 â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) + â â + = 2 2 2 2 5 4 1 2 3 x y
- 13. Hyperbolas âŦ Example: Graph Center (â5, 4) opens in y-direction rx = 2, ry = 3 ï vertices ïą3 slope of asymptotes: â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) + â â + = 2 2 2 2 5 4 1 2 3 x y ïą 3 2
- 14. Hyperbolas âŦ Example: Graph Center (â5, 4) opens in y-direction rx = 2, ry = 3 ï vertices ïą3 slope of asymptotes: â + + + = 2 2 9 4 90 32 197 0 x y x y ( ) ( ) + â â + = 2 2 2 2 5 4 1 2 3 x y ïą 3 2
- 15. Focal Length âŦ In an ellipse, the sum of the distances from a point on the ellipse to the two foci is constant, but in a hyperbola, itâs the difference between the distances that is constant. âŦ To find the focal radius, we can use the Pythagorean Theorem. âŦ Notice that c > a for the hyperbola. a b c âĒ = + 2 2 2 c a b
- 16. Classwork âŦ College Algebra 2e âŦ 8.2: 12-44 (Ã4); 8.1: 32-56 (Ã4); 7.8: 36-44 (Ã4) âŦ 8.2 Classwork Check âŦ Quiz 8.1