8.3 p value
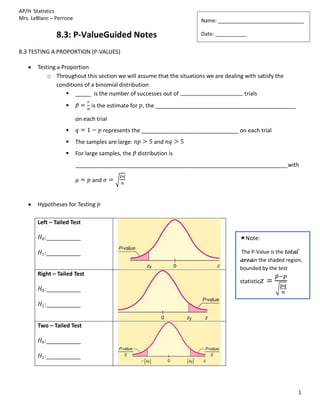
- 1. AP/H Statistics Mrs. LeBlanc – Perrone Name: ______________________________ 8.3: P-ValueGuided Notes Date: ___________ 8.3 TESTING A PROPORTION (P-VALUES) Testing a Proportion o Throughout this section we will assume that the situations we are dealing with satisfy the conditions of a binomial distribution  _____ is the number of successes out of trials  is the estimate for , the _____________________________________________ on each trial  represents the _______________________________ on each trial  The samples are large: and  For large samples, the distribution is ____________________________________________________________________with and Hypotheses for Testing Left – Tailed Test :___________ Note: :___________ The P-Value is the total areain the shaded region, bounded by the test Right – Tailed Test statistic :___________ :___________ Two – Tailed Test :___________ :___________ 1
- 2. AP/H Statistics Mrs. LeBlanc – Perrone How to Test 1. ______________________________________________________________________________  Is this a binomial experiment with trials?  Does represent the probability of success?  Identify  Is the sample large? (Is and ?) (Use p from )  If yes, then the distribution can be approximated by the normal distribution 2. ______________________________________________________________________________ ______________________________________________________________________________ 3. ______________________________________________________________________________ ______________________________________________________________________________  Sample Test Statistic: 4. ____________________________________________________________________________ ______________________________________________________________________________  use the standard normal distribution 5. ______________________________________________________________________________  If P-value , we reject  If P-value > , we fail to reject 6. ______________________________________________________________________________ 2
- 3. AP/H Statistics Mrs. LeBlanc – Perrone o Example: Testing A team of eye surgeons has developed a new technique for a risky eye operation to restore the sight of people blinded from a certain disease. Under the old method, it is known that only 30% of the patients who undergo this operation recover their eyesight. Suppose that surgeons in various hospitals have performed a total of 225 operations using the new method and that 88 have been successful (i.e., the patients fully recovered their sight). Can we justify the claim that the new method is better than the old one? (Use a 1% level of significance.) 3
- 4. AP/H Statistics Mrs. LeBlanc – Perrone Summary Questions 1. How is testing (using P-values) similar to testing (using P-values)? ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ 2. How do you find the total area in each tail, when testing using P-values? (Choose one method: using the table or using the calculator. Hint: it’s a similar process to what we did in chapter 6) ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ 3. What does it mean to “reject” or “fail to reject” ? (Hint: see section 8.1) ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ ____________________________________________________________________________________ “HOT” Question: __________________________________________________________________________________________ __________________________________________________________________________________________ 4