A Comparison Study of KGD, PKN and a Modified P3D Model II.
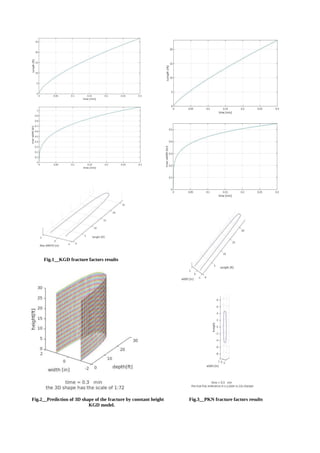
- 1. A Comparison Study of KGD, PKN and a Modified P3D Model. Arash Nasirisavadkouhi, International Campus of Sharif University of Technology. Abstract The paper is aiming to represent the growth of a fracture to its final shape at a specific time. 2D models i.e KGD and PKN which most of the early hydraulic fractures were designed by applying one of these models were analyzed, compared and their equations solved. Moreover a P3D model is modified to give true 3D results. By assuming elliptical growth of the fracture and not the circular growth, a more realistic results generated. It is prudent to notice that the elliptic behavior which the fracture growing is representing has changing parameters at any moment, means the growth of a fracture in a specific period of time even in its simplest form does not obey a simple mathematical equation. This study does not cover propagation models. Keywords. PKN, KGD, 2D fracture models, modified P3D fracture model, elliptical fracture growth, Matlab. Introduction and Methodology The design of a fracture process usually includes at least three stages: fracture geometry prediction, fracture clean up prediction and well performance prediction. This study covers partially the first and second items. The dimension and propagation characteristics of a hydraulic fracture are important information in the design of fracturing operations. Knowing the properties of reservoir rock, fracture fluid and the magnitude and direction of in-situ stress, one seeks an accurate prediction of the dimension (opening width, length, and height) of the hydraulically induced fracture for a given pumping rate and time. Many fracture models have been developed for this purpose. the minimum in-situ stress is in the horizontal plane, the fracture is a vertical fracture whose plane is perpendicular to the minimum in-situ stress. There are two factors that control the vertical growth of a hydraulic fracture. They are: (1) the contrast in material properties, and (2) the contrast in vertical distribution of in-situ stress. Since the plane of hydraulic fracture is perpendicular to the minimum horizontal in-situ stress, the growth of fracture height is controlled by the vertical distribution of the horizontal minimum in-situ stress. When the contrast of stresses between adjacent stress zones is large, the growth of fracture height is expected to be contained. There are two basic constant height models: the Khristinaovic-Geertsma- de Klerk, KGD model, and the Perkins-Kem-Nordgren, PKN model. Most of the early hydraulic fractures were designed by applying one of these models. The underlying mechanics in these two models differs significantly. In principle, the pseudo 3-D models may be regarded as an extension of the KGD or the PKN models and include the fracture height growth. The simplest approach has been to determine the fracture height from the local net fluid pressure, in-situ stress contrast, and rock toughness by satisfying the local static equilibrium. A constant fluid pressure is usually assumed over the vertical cross section of the fracture and the fluid flow is one dimensional along the direction of pay zone. The assumption of one dimensional fluid flow inside the fracture creates an inconsistency in the calculation of fracture height growth. The 2D fracture models have been reasonably successful in practical simulation with a simplified calculation. However, they have limitations force us to use improved models. A pseudo 3D model can indeed provide useful information on the behavior of a hydraulically induced fracture and solve that problems regarding to 2D models to an extent, Although the model has been proven to be a valuable tool in fracture design, one has to bear in mind that, under certain circumstances such as a formation which has a complex in-situ stress distribution, the pseudo 3D fracture model may not be capable of capturing all important features due to the approximate nature of the model. Generally it is of little interest to practical application nowadays. Table.2 gives the necessary data of the the mentioned models. To have a true 3D model some modifications should be made to the original circular model. Circular models are calledŌĆ£pseudo,ŌĆØ because they do not consider the variation of fracture geometry in a three dimensional space, rather it modifies the 2D (PKN) model by adding height variation along the fracture length and its effect on the fracture width. Now if we assume that at any moment the fracture limit geometry follows the shape of one half of ellipse which its minor axis vertices intersect with the fracture opening and its major axis vertex is the depth of penetration, we have omitted the ŌĆ£constant fluid pressure assumption over the vertical cross sectionŌĆØ . It should be mentioned that an elliptical shape is a theoretical guess and the true shape of the fracture is only revealed by having the exact stress and strength distribution of the rock. The stress interference around neighboring perforations causes fracture initiation, the angle between the perforation orientation and the maximum principal stress can also affect fracture shape in addition to what is mentioned previously. Fig.1 represents the predicted shape of the fracture. Using the data in Table.1 a fracture growth were represented. Table 1-Fracture Properties and Material Parameters Shear modulus [psi] Drained Poisson's ratio Fluid viscosity [cp] In-situ stress [psi] Pumping rate [bbl/min] Wellbore radius [ft] Passed Time (as an input by user) [min] G=8.702*1e5 v=.2 mu=1 Žāmin=4000 Q=75 rw=.3 tf=.3 Modeling Results Fig.1 indicates that the fracture length increases with higher rate than the fracture opening width which increases in proportional to t (1/3) . After 18 seconds of fracture growth, the ratio of the final L/W equals 300, indicates a sharp curvy tip which in turn approves the low effect of the tip geometry on fracture growth in these models. Geertsma and de Klerk argue that since the tip is a local singularity of the fracture, its effect on the overall fracture geometry should be small and their solution is a good Spring 2015 This paper was prepared for the advanced well-Stimulation course at SUT_international Campus and is published on-line based on educational purposes.
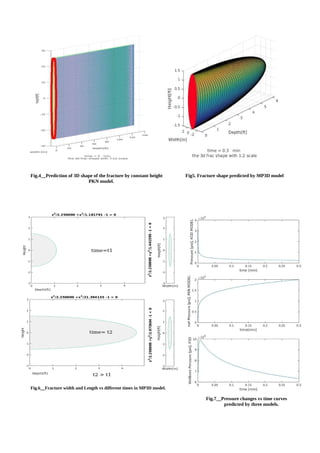
- 2. approximation for the fracture opening width and the overall fracture length. Please notice that the the true shape of the tip is sharper than what is seen in Figs.1 through 6 but due to inequality of dimensions of the coordinates its true shape is somehow concealed, besides representing the true ratios does not show the 3d shape satisfactorily. Scales can be manipulated in the written scripts easily using 'daspect' code to gain different views of the fracture. What is explained for Fig.1 can be true for Fig.3 to some extent too. In deed although the underlying mechanics in PKN and KGB models differ significantly, Under similar assumptions (no leak of) they yield similar results, however their difference in predicted widths can not be neglected. There is another glaring inconsistency in the final 3d shapes. yz-plane in Fig.2 is a rectangular, means the 3d surface is a extension of the xy-plane diagram into 3d space, however the 3d surface in Fig.4 follows a semi parabola in xy-plane and a semi-ellipse in yz-plane. Every cross section perpendicular to x- axis cuts the surface in the semi-ellipse: (L(time),W(time),H). It is prudent to notice that the ellipse equation of z 2 a 2 + y 2 b 2 =1 has changing constant variable b (and a, if height is not constant) at any moment, means the growth of a fracture in a specific period of time even in its simplest form does not obey a simple mathematical equation. However eventually this modified pseudo three dimensional model predicts a complete ellipsoid in 3D space at specific time which can be seen in the Fig.5. Fig.6 compares the predicted width and length by P3D model at different moments. As can be seen, initially (at t1) the shape of length-time plane of the fracture is close to a circle but the more time passes and the deeper fracture is, it is forming into the shape of an ellipse. This 'circle to ellipse phenomenon' is not much noticeable in the yz-plane due to the weight of t in related equations. Figs. 5 and 6 also reveals once more the uniform stress surrounding the fracture area. It is interesting to note in Fig.7 that the wellbore pressure predicted by the PKN model, in contrast to the KGD model, rises as the fracture length increases. However the pressure predicted by KGD will approach to in-situ stress Žāmin for a large value of length. Initially the difference between two 2D models prediction of pressure is noticeable however as time passes the difference reaches a constant maximum. Table 2- 2D and 3D Models Description Model:KGD/2D The model is best suited for fractures whose length/height ratio is near unity or less. Hence: Height=1.1*final lengthEquations: L=0.48( 8GQ3 (1ŌłÆv)╬╝ ) (1/6) .t (2/3) Wo=1.32( 8(1ŌłÆv)Q 3 ╬╝ G ) (1/6) .t(1/3) Pw=Žāmin+0.96( 2G 3 Q╬╝ (1ŌłÆv) 3 L 2 ) (1/4) Assumptions -Constant height assumption -The fracture is at a plane strain condition in the horizontal plane -The fracture tip is a cusp-shaped tip -Hydraulic fracture fluid is viscous and Newtonian -Elasticity theory applied -No leak off Model:PKN/2D The model is generally regarded to be best suited for fractures whose length/height ratio is large. Hence: Height=0.2*final lengthEquations: L=0.68( GQ3 (1ŌłÆv)╬╝ h 4 ) (1/ 5) .t(4/ 5) Wo=2.5( (1ŌłÆv)Q 2 ╬╝ G.h ) (1/5) .t (1/5) Pw=2.5( G4 Q2 ╬╝ (1ŌłÆv) 4 h 6 ) (1/5) .t(1/5) Assumptions: -The fracture is at a state of plane strain in the vertical plane and the vertical fracture cross-section is elliptical -The fracture toughness has no effect on the fracture geometry -No leak off Model:Modified P3D Constant Height=3 ft. Equations: Peneterationdepth(R)=0.548( GQ3 ╬╝ ) (1/9) .t (1/9) Wo=1.32( 8(1ŌłÆv)Q 3 ╬╝ G ) (1/6) .t(1/3) Pw=ŽāminŌłÆ 5 4ŽĆ G wo R ln (rw) R Assumptions: -Vertical distribution of the minimum in-situ stress is uniform. -Fracture growth follows elliptical shape. -No leak off
- 3. Fig.1__KGD fracture factors results Fig.2__Prediction of 3D shape of the fracture by constant height Fig.3__PKN fracture factors results KGD model.
- 4. Fig.4__Prediction of 3D shape of the fracture by constant height Fig5. Fracture shape predicted by MP3D model PKN model. Fig.6__Fracture width and Length vs different times in MP3D model. Fig.7__Pressure changes vs time curves predicted by three models.
- 5. Further study. This study can be used for further researches of fracture propagations modeling. Useful Matlab codes for Visualization: ezplot ('equation'): The easiest way to express a function is via a string: ezplot('x.*y + x.^2 - y.^2 ŌĆō 1') ezplot(sprintf('equation with changing variables',(h/2)^2,(W0(end)/2)^2),[xmin xmax ymin ymax]); isosurface: This code draws a 3-D volume in the space which is very helpful. set(figure name,'name','title','numbertitle','off'): Change the title of a figure. daspect([1,2,3]): Can change data aspect ratio. plot3(x,y,z): Were used to plot 2d diagrams in 3d space. References. 1. Ching H.Yew(1997) ŌĆ£Mechanic of Hydraulic fracturingŌĆØ, Chapters 1 & 2 2. A. and Cleary, M.P. 1986. Development and Testing of a Pseudo-three- dimensional Model of Hydraulic Fracture Geometry. SPE Prod. Eng. 1 (6) 449- 466. 3. N.R Warpinsky. Abu-Sayed.(1993) ŌĆ£Hydraulic Fracture model comparison study: complete resultsŌĆØ Acknowledgements Special Thanks to Mr.Andrey Vikharev who noticed a misprint in the initial version of this article. Matlab scripts. function fracture2DP3D %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % KGD,PKN (2Ds) and a modified P3D models are solved and compared in this % % script using the data of Mechanic of Hydraulic Fracturing(Ching H.Yew) % % chapters 1 and 2. % % % % 06/2015 by Arash Nasiri % % arash.nasiris@gmail.com % % Feel free to modify for teaching and learning. % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear all;clc; %----------------------------------------------------------------------- G=8.702*1e5; % Shear modulus [psi] v=.2; % Drained Poisson's ratio mu=1; % Fluid viscosity [cp] Zi=4000; % In-situ stress [psi] Q=75; % Pumping rate [bbl/min] h=3; % Fracture height [ft] rw=.3; % Wellbore radius [ft] tf=input('How much time is passed? n hint best results 0.5<t<10 n Enter time as min(0.25<=t):'); tic; %**** [Tkgd,pkgd]=KGD(tf,G,Q,v,mu,Zi);% KGD %**** [Tpkn,ppkn]=PKN(tf,G,Q,v,mu,h);% PKN %**** [T3,p3]=TD(tf,G,Q,mu,Zi,rw,h);% P3D %**** figure(1) set(1,'name','WELLBORE PRESSURE vs TIME in 2D and P3D MODELS','numbertitle','off') subplot(311) plot(pkgd,Tkgd); ylabel('Pressure [psi], KGD MODEL'); xlabel('time [min]'); subplot(312) plot(ppkn,Tpkn) ylabel('net Pressure [psi], PKN MODEL'); xlabel('time[min]'); subplot(313) plot(p3,T3) ylabel('Wellbore Pressure [psi], P3D') xlabel('time [min]') toc disp('Auf wieder sehen') end * function [P,T]= KGD(tf,G,Q,v,mu,Zi) %**** %------------- KGB ------------- %**** for t0=tf/50:tf/50:tf %time step for visualization i=1; for t=0:.0001:t0 ngr(i)=0; L(i)=.48*(8*G*Q^3/((1-v)*mu))^(1/6)*t^(2/3); %Fracture Length W0(i)=1.32*(8*(1-v)*mu*Q^3/G)^(1/6)*t^(1/3); %maximum fracture opening width Pw=Zi+0.96*(2*Q*mu*G^3/((1-v)^3*L(i)^2))^(1/4); %wellbore pressure Pwi(i)=Pw; time(i)=t; i=i+1; end figure(10); set(10,'name','KGD frac growth and final shape','numbertitle','off'); drawnow; limitL=.48*(8*G*Q^3/((1-v)*mu))^(1/6)*tf^(2/3); %used for axis limits limitW0=1.32*(8*(1-v)*mu*Q^3/G)^(1/6)*tf^(1/3); h=1.1*limitL; subplot(221); plot(time,L); ylabel('Length [ft]'); xlabel('time [min]'); axis([0 tf 0 limitL]); subplot(222); plot(time,W0); ylabel('max width [in]'); xlabel('time [min]'); axis([0 tf 0 limitW0]);
- 6. grid on; subplot(224); fL=fliplr(L); plot3(fL,W0,ngr,'b'); hold; plot3(fL,-W0,ngr,'b'); hold; axis([0 limitL -2*limitW0 2*limitW0 -1 1]); grid on; ylabel('Max WIDTH [in]') xlabel('length [ft]') set(gca,'ztick',[]); daspect([1,1/2,1]); view(-62,26); [~,h3]=suplabel(sprintf('time = %0.1g min',t0));grid on; hold off; end subplot(223); hold; for I=0:h/100:h plot3(fL,W0,ngr+I); plot3(fL,-W0,ngr+I); end daspect([1,1/6,1]); view(-56,28); ylabel('width [in]') zlabel('height[ft]') xlabel('depth[ft]') [~,h3]=suplabel(sprintf('time = %0.1g min n the 3D shape has the scale of 1:72',t0));grid on; T=time;P=Pwi; end function [P,T]= PKN(tf,G,Q,v,mu,h) %**** %------------- PKN (Assuming no leak off) ------- %**** for t0=tf/50:tf/50:tf %time step for visualization i=1; for t=0:.001:t0 ngr(i)=0; L(i)=.68*(G*Q^3/((1-v)*mu*h^4))^(1/5)*t^(4/5); %Fracture Length W0(i)=2.5*((1-v)*mu*Q^2/(G*h))^(1/5)*t^(1/5); %Fracture opening width Pw=2.5*(Q^2*mu*G^4/((1-v)^4*h^6))^(1/5)*t^(1/5); %wellbore net pressure Pwi(i)=Pw; time(i)=t; i=i+1; end timer=fliplr(time); limitL=.68*(G*Q^3/((1-v)*mu*h^4))^(1/5)*tf^(4/5); %used for axis limits limitW0=2.5*((1-v)*mu*Q^2/(G*h))^(1/5)*tf^(1/5); h2=0.2*limitL; z=h2/time(end).*time+h2/2; A=G*Q^3/((1-v)*mu*h2^4);a=.68^(5/4)*A; B=((1-v)*mu*Q^2)/(G*h2);b=2.5^5*B; c=h2/time(end);Z=z-h2/2-t0*c; figure(20) set(20,'name','PKN frac growth and enterance','numbertitle','off') drawnow; subplot(221) plot(time,L) ylabel('Length [ft]') xlabel('time [min]') axis([0 tf 0 limitL]) grid on; subplot(222) plot(time,W0) ylabel('max width [in]') xlabel('time [min]') axis([0 tf 0 limitW0]) grid on; subplot(224) fL=fliplr(L); plot3(fL,W0,ngr,'b'); hold; plot3(fL,-W0,ngr,'b'); hold; axis([0 limitL -2*limitW0 2*limitW0 -1 1]); grid on; ylabel('width [in]') xlabel('Length [ft]') set(gca,'ztick',[]); daspect([1,1/2,1]); view(-53,56) [~,h3]=suplabel(sprintf('time = %0.1g min n PKN RESULTS n',t0));grid on; hold off; end figure(20) subplot(223) plot3(ngr,W0,-z+1.5*h2,'b'); hold; plot3(ngr,-W0,-z+1.5*h2,'b'); plot3(ngr,W0,z-1.5*h2,'b'); plot3(ngr,-W0,z-1.5*h2,'b'); axis([-1 1 -2*limitW0 2*limitW0 -2*h2 2*h2]); grid on; ylabel('width [in]') zlabel('height') set(gca,'xtick',[]); daspect([1,1,1]); view(-60,20) [~,h3]=suplabel(sprintf('time = %0.1g min n the true frac enterance in z-y plane is 12x sharpern',t0));grid on;
- 7. hold off; figure(21) set(21,'name','PKN final shape','numbertitle','off') hold; for I=0:h2/100:h2; plot3(fL,W0,ngr+I,'g'); plot3(fL,-W0,ngr+I,'b'); plot3(fL,W0,-ngr-I,'g'); plot3(fL,-W0,-ngr-I,'b'); grid on; ylabel('width [in]') zlabel('height[ft]') xlabel('depth[ft]') set(gca,'ytick',[]); daspect([1,5.5,1]); view(-77,4) end; plot3(ngr,W0,-z+1.5*h2,'r*'); plot3(ngr,-W0,-z+1.5*h2,'r*'); plot3(ngr,W0,z-1.5*h2,'r*'); plot3(ngr,-W0,z-1.5*h2,'r*'); [~,h3]=suplabel(sprintf('time = %0.1g min n the 3d frac shape with 7:12 scale n',t0));grid on; T=time;P=Pwi; end *** function [P,T]= TD(tf,G,Q,mu,Zi,rw,h) %**** %------------- Geertsma de Klerk (P3D) ------- %**** for t0=tf/50:tf/50:tf %time step for visualization i=1; for t=0:.001:t0 ngr(i)=0; R(i)=.548*(G*Q^3/mu)^(1/9)*t^(4/9); %Fracture radius W0(i)=21*(mu^2*Q^3/G^2)^(1/9)*t^(1/9); %Maximum fracture opening width Pw=Zi-5/(4*pi)*(G*W0(i)/R(i))*log(rw/R(i)); %wellbore net pressure Pwi(i)=Pw; time(i)=t; i=i+1; end figure(30) set(30,'name','P3D frac growth-(R vs t) (W vs t)','numbertitle','off') drawnow; limitRi=.548*(G*Q^3/mu)^(1/9)*tf^(4/9); %used for axis limits limitW0=21*(mu^2*Q^3/G^2)^(1/9)*tf^(1/9); subplot(221) ezplot(sprintf('z.^2/%f +x.^2/%f -1',(h/2)^2,(R(end))^2),[-0 limitRi -h h]); ylabel('Height') xlabel('Depth[ft]') subplot(222) ezplot(sprintf('z.^2/%f +y.^2/%f -1',(h/2)^2,(W0(end)/2)^2),[-limitW0 limitW0 -h h]); ylabel('Heigth[ft]') xlabel('Width[in]') daspect([12,1,1]); set(gca,'xtick',[]) subplot(224) hold; A=R(end);B=W0(end)/2;C=h/2; tp = linspace(0,2*pi,100); pp = linspace(0,pi,100); [T,P] = meshgrid(tp,pp); x = A*cos(T).*cos(P); y = B*cos(T).*sin(P); z = C*sin(T); surf(x,y,z); daspect([1,6,1]); view(-51,22) xlabel('Depth[ft]'); ylabel('Width[in]'); zlabel('Height[ft]'); axis([0,limitRi,-limitW0,limitW0,-h/2,h/2]); end clearvars ngr tp tt T P y z i tp = linspace(0,2*pi,1000); pp = linspace(0,pi,1000); [T,P] = meshgrid(tp,pp); y = B*cos(T).*sin(P); z= C*sin(T); for i=1:length(y) ngr(i)=0; end hold; plot3(ngr,y,z,'r') daspect([1,6,1]); view(-51,22) [~,h3]=suplabel(sprintf('time = %0.1g min n the 3d frac shape with 1:2 scale n',t0));grid on; T=time;P=Pwi; end

![A Comparison Study of KGD, PKN
and a Modified P3D Model.
Arash Nasirisavadkouhi, International Campus of Sharif University of
Technology.
Abstract
The paper is aiming to represent the growth of a fracture to its
final shape at a specific time. 2D models i.e KGD and PKN
which most of the early hydraulic fractures were designed by
applying one of these models were analyzed, compared and
their equations solved. Moreover a P3D model is modified to
give true 3D results. By assuming elliptical growth of the
fracture and not the circular growth, a more realistic results
generated. It is prudent to notice that the elliptic behavior which
the fracture growing is representing has changing parameters at
any moment, means the growth of a fracture in a specific
period of time even in its simplest form does not obey a simple
mathematical equation. This study does not cover propagation
models.
Keywords.
PKN, KGD, 2D fracture models, modified P3D fracture model,
elliptical fracture growth, Matlab.
Introduction and Methodology
The design of a fracture process usually includes at least three
stages: fracture geometry prediction, fracture clean up
prediction and well performance prediction. This study covers
partially the first and second items. The dimension and
propagation characteristics of a hydraulic fracture are important
information in the design of fracturing operations. Knowing the
properties of reservoir rock, fracture fluid and the magnitude
and direction of in-situ stress, one seeks an accurate prediction
of the dimension (opening width, length, and height) of the
hydraulically induced fracture for a given pumping rate and
time. Many fracture models have been developed for this
purpose. the minimum in-situ stress is in the horizontal plane,
the fracture is a vertical fracture whose plane is perpendicular to
the minimum in-situ stress. There are two factors that control
the vertical growth of a hydraulic fracture. They are:
(1) the contrast in material properties, and (2) the contrast in
vertical distribution of in-situ stress.
Since the plane of hydraulic fracture is perpendicular to the
minimum horizontal in-situ stress, the growth of fracture height
is controlled by the vertical distribution of the horizontal
minimum in-situ stress. When the contrast of stresses between
adjacent stress zones is large, the growth of fracture height is
expected to be contained. There are two basic constant height
models: the Khristinaovic-Geertsma- de Klerk, KGD model,
and the Perkins-Kem-Nordgren, PKN model. Most of the early
hydraulic fractures were designed by applying one of these
models. The underlying mechanics in these two models differs
significantly.
In principle, the pseudo 3-D models may be regarded as an
extension of the KGD or the PKN models and include the
fracture height growth. The simplest approach has been to
determine the fracture height from the local net fluid pressure,
in-situ stress contrast, and rock toughness by satisfying the local
static equilibrium. A constant fluid pressure is usually assumed
over the vertical cross section of the fracture and the fluid flow
is one dimensional along the direction of pay zone. The
assumption of one dimensional fluid flow inside the fracture
creates an inconsistency in the calculation of fracture height
growth. The 2D fracture models have been reasonably
successful in practical simulation with a simplified calculation.
However, they have limitations force us to use improved
models. A pseudo 3D model can indeed provide useful
information on the behavior of a hydraulically induced fracture
and solve that problems regarding to 2D models to an extent,
Although the model has been proven to be a valuable tool in
fracture design, one has to bear in mind that, under certain
circumstances such as a formation which has a complex in-situ
stress distribution, the pseudo 3D fracture model may not be
capable of capturing all important features due to the
approximate nature of the model. Generally it is of little interest
to practical application nowadays. Table.2 gives the necessary
data of the the mentioned models.
To have a true 3D model some modifications should be made to
the original circular model. Circular models are calledŌĆ£pseudo,ŌĆØ
because they do not consider the variation of fracture geometry
in a three dimensional space, rather it modifies the 2D (PKN)
model by adding height variation along the fracture length and
its effect on the fracture width. Now if we assume that at any
moment the fracture limit geometry follows the shape of one
half of ellipse which its minor axis vertices intersect with the
fracture opening and its major axis vertex is the depth of
penetration, we have omitted the ŌĆ£constant fluid pressure
assumption over the vertical cross sectionŌĆØ . It should be
mentioned that an elliptical shape is a theoretical guess and the
true shape of the fracture is only revealed by having the exact
stress and strength distribution of the rock. The stress
interference around neighboring perforations causes fracture
initiation, the angle between the perforation orientation and the
maximum principal stress can also affect fracture shape in
addition to what is mentioned previously. Fig.1 represents the
predicted shape of the fracture. Using the data in Table.1 a
fracture growth were represented.
Table 1-Fracture Properties and Material Parameters
Shear modulus [psi]
Drained Poisson's ratio
Fluid viscosity [cp]
In-situ stress [psi]
Pumping rate [bbl/min]
Wellbore radius [ft]
Passed Time (as an input by user) [min]
G=8.702*1e5
v=.2
mu=1
Žāmin=4000
Q=75
rw=.3
tf=.3
Modeling Results
Fig.1 indicates that the fracture length increases with higher rate
than the fracture opening width which increases in proportional
to t
(1/3)
.
After 18 seconds of fracture growth, the ratio of the final L/W
equals 300, indicates a sharp curvy tip which in turn approves
the low effect of the tip geometry on fracture growth in these
models. Geertsma and de Klerk argue that since the tip is a local
singularity of the fracture, its effect on the overall fracture
geometry should be small and their solution is a good
Spring 2015
This paper was prepared for the advanced well-Stimulation course at SUT_international Campus and is published on-line based on educational purposes.](https://image.slidesharecdn.com/ef819075-8889-4c09-9d6d-bcf177eabbf7-150903161232-lva1-app6892/85/A-Comparison-Study-of-KGD-PKN-and-a-Modified-P3D-Model-II-1-320.jpg)

![Further study.
This study can be used for further researches of fracture
propagations modeling.
Useful Matlab codes for Visualization:
ezplot ('equation'): The easiest way to express a function is via a string:
ezplot('x.*y + x.^2 - y.^2 ŌĆō 1')
ezplot(sprintf('equation with changing variables',(h/2)^2,(W0(end)/2)^2),[xmin
xmax ymin ymax]);
isosurface: This code draws a 3-D volume in the space which is very helpful.
set(figure name,'name','title','numbertitle','off'): Change the title of a figure.
daspect([1,2,3]): Can change data aspect ratio.
plot3(x,y,z): Were used to plot 2d diagrams in 3d space.
References.
1. Ching H.Yew(1997) ŌĆ£Mechanic of Hydraulic fracturingŌĆØ,
Chapters 1 & 2
2. A. and Cleary, M.P. 1986. Development and Testing of a
Pseudo-three- dimensional Model of Hydraulic Fracture
Geometry. SPE Prod. Eng. 1 (6) 449- 466.
3. N.R Warpinsky. Abu-Sayed.(1993) ŌĆ£Hydraulic Fracture
model comparison study: complete resultsŌĆØ
Acknowledgements
Special Thanks to Mr.Andrey Vikharev who noticed a misprint in
the initial version of this article.
Matlab scripts.
function fracture2DP3D
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% KGD,PKN (2Ds) and a modified P3D models are solved and compared in this %
% script using the data of Mechanic of Hydraulic Fracturing(Ching H.Yew) %
% chapters 1 and 2. %
% %
% 06/2015 by Arash Nasiri %
% arash.nasiris@gmail.com %
% Feel free to modify for teaching and learning. %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;clc;
%-----------------------------------------------------------------------
G=8.702*1e5; % Shear modulus [psi]
v=.2; % Drained Poisson's ratio
mu=1; % Fluid viscosity [cp]
Zi=4000; % In-situ stress [psi]
Q=75; % Pumping rate [bbl/min]
h=3; % Fracture height [ft]
rw=.3; % Wellbore radius [ft]
tf=input('How much time is passed? n hint best results 0.5<t<10 n Enter time as min(0.25<=t):');
tic;
%****
[Tkgd,pkgd]=KGD(tf,G,Q,v,mu,Zi);% KGD
%****
[Tpkn,ppkn]=PKN(tf,G,Q,v,mu,h);% PKN
%****
[T3,p3]=TD(tf,G,Q,mu,Zi,rw,h);% P3D
%****
figure(1)
set(1,'name','WELLBORE PRESSURE vs TIME in 2D and P3D MODELS','numbertitle','off')
subplot(311)
plot(pkgd,Tkgd);
ylabel('Pressure [psi], KGD MODEL');
xlabel('time [min]');
subplot(312)
plot(ppkn,Tpkn)
ylabel('net Pressure [psi], PKN MODEL');
xlabel('time[min]');
subplot(313)
plot(p3,T3)
ylabel('Wellbore Pressure [psi], P3D')
xlabel('time [min]')
toc
disp('Auf wieder sehen')
end
*
function [P,T]= KGD(tf,G,Q,v,mu,Zi)
%****
%------------- KGB -------------
%****
for t0=tf/50:tf/50:tf %time step for visualization
i=1;
for t=0:.0001:t0
ngr(i)=0;
L(i)=.48*(8*G*Q^3/((1-v)*mu))^(1/6)*t^(2/3); %Fracture Length
W0(i)=1.32*(8*(1-v)*mu*Q^3/G)^(1/6)*t^(1/3); %maximum fracture opening width
Pw=Zi+0.96*(2*Q*mu*G^3/((1-v)^3*L(i)^2))^(1/4); %wellbore pressure
Pwi(i)=Pw;
time(i)=t;
i=i+1;
end
figure(10);
set(10,'name','KGD frac growth and final shape','numbertitle','off');
drawnow;
limitL=.48*(8*G*Q^3/((1-v)*mu))^(1/6)*tf^(2/3); %used for axis limits
limitW0=1.32*(8*(1-v)*mu*Q^3/G)^(1/6)*tf^(1/3);
h=1.1*limitL;
subplot(221);
plot(time,L);
ylabel('Length [ft]');
xlabel('time [min]');
axis([0 tf 0 limitL]);
subplot(222);
plot(time,W0);
ylabel('max width [in]');
xlabel('time [min]');
axis([0 tf 0 limitW0]);](https://image.slidesharecdn.com/ef819075-8889-4c09-9d6d-bcf177eabbf7-150903161232-lva1-app6892/85/A-Comparison-Study-of-KGD-PKN-and-a-Modified-P3D-Model-II-5-320.jpg)
![grid on;
subplot(224);
fL=fliplr(L);
plot3(fL,W0,ngr,'b');
hold;
plot3(fL,-W0,ngr,'b');
hold;
axis([0 limitL -2*limitW0 2*limitW0 -1 1]);
grid on;
ylabel('Max WIDTH [in]')
xlabel('length [ft]')
set(gca,'ztick',[]);
daspect([1,1/2,1]);
view(-62,26);
[~,h3]=suplabel(sprintf('time = %0.1g min',t0));grid on;
hold off;
end
subplot(223);
hold;
for I=0:h/100:h
plot3(fL,W0,ngr+I);
plot3(fL,-W0,ngr+I);
end
daspect([1,1/6,1]);
view(-56,28);
ylabel('width [in]')
zlabel('height[ft]')
xlabel('depth[ft]')
[~,h3]=suplabel(sprintf('time = %0.1g min n the 3D shape has the scale of 1:72',t0));grid on;
T=time;P=Pwi;
end
function [P,T]= PKN(tf,G,Q,v,mu,h)
%****
%------------- PKN (Assuming no leak off) -------
%****
for t0=tf/50:tf/50:tf %time step for visualization
i=1;
for t=0:.001:t0
ngr(i)=0;
L(i)=.68*(G*Q^3/((1-v)*mu*h^4))^(1/5)*t^(4/5); %Fracture Length
W0(i)=2.5*((1-v)*mu*Q^2/(G*h))^(1/5)*t^(1/5); %Fracture opening width
Pw=2.5*(Q^2*mu*G^4/((1-v)^4*h^6))^(1/5)*t^(1/5); %wellbore net pressure
Pwi(i)=Pw;
time(i)=t;
i=i+1;
end
timer=fliplr(time);
limitL=.68*(G*Q^3/((1-v)*mu*h^4))^(1/5)*tf^(4/5); %used for axis limits
limitW0=2.5*((1-v)*mu*Q^2/(G*h))^(1/5)*tf^(1/5);
h2=0.2*limitL;
z=h2/time(end).*time+h2/2;
A=G*Q^3/((1-v)*mu*h2^4);a=.68^(5/4)*A;
B=((1-v)*mu*Q^2)/(G*h2);b=2.5^5*B;
c=h2/time(end);Z=z-h2/2-t0*c;
figure(20)
set(20,'name','PKN frac growth and enterance','numbertitle','off')
drawnow;
subplot(221)
plot(time,L)
ylabel('Length [ft]')
xlabel('time [min]')
axis([0 tf 0 limitL])
grid on;
subplot(222)
plot(time,W0)
ylabel('max width [in]')
xlabel('time [min]')
axis([0 tf 0 limitW0])
grid on;
subplot(224)
fL=fliplr(L);
plot3(fL,W0,ngr,'b');
hold;
plot3(fL,-W0,ngr,'b');
hold;
axis([0 limitL -2*limitW0 2*limitW0 -1 1]);
grid on;
ylabel('width [in]')
xlabel('Length [ft]')
set(gca,'ztick',[]);
daspect([1,1/2,1]);
view(-53,56)
[~,h3]=suplabel(sprintf('time = %0.1g min n PKN RESULTS n',t0));grid on;
hold off;
end
figure(20)
subplot(223)
plot3(ngr,W0,-z+1.5*h2,'b');
hold;
plot3(ngr,-W0,-z+1.5*h2,'b');
plot3(ngr,W0,z-1.5*h2,'b');
plot3(ngr,-W0,z-1.5*h2,'b');
axis([-1 1 -2*limitW0 2*limitW0 -2*h2 2*h2]);
grid on;
ylabel('width [in]')
zlabel('height')
set(gca,'xtick',[]);
daspect([1,1,1]);
view(-60,20)
[~,h3]=suplabel(sprintf('time = %0.1g min n the true frac enterance in z-y plane is 12x sharpern',t0));grid on;](https://image.slidesharecdn.com/ef819075-8889-4c09-9d6d-bcf177eabbf7-150903161232-lva1-app6892/85/A-Comparison-Study-of-KGD-PKN-and-a-Modified-P3D-Model-II-6-320.jpg)
![hold off;
figure(21)
set(21,'name','PKN final shape','numbertitle','off')
hold;
for I=0:h2/100:h2;
plot3(fL,W0,ngr+I,'g');
plot3(fL,-W0,ngr+I,'b');
plot3(fL,W0,-ngr-I,'g');
plot3(fL,-W0,-ngr-I,'b');
grid on;
ylabel('width [in]')
zlabel('height[ft]')
xlabel('depth[ft]')
set(gca,'ytick',[]);
daspect([1,5.5,1]);
view(-77,4)
end;
plot3(ngr,W0,-z+1.5*h2,'r*');
plot3(ngr,-W0,-z+1.5*h2,'r*');
plot3(ngr,W0,z-1.5*h2,'r*');
plot3(ngr,-W0,z-1.5*h2,'r*');
[~,h3]=suplabel(sprintf('time = %0.1g min n the 3d frac shape with 7:12 scale n',t0));grid on;
T=time;P=Pwi;
end
***
function [P,T]= TD(tf,G,Q,mu,Zi,rw,h)
%****
%------------- Geertsma de Klerk (P3D) -------
%****
for t0=tf/50:tf/50:tf %time step for visualization
i=1;
for t=0:.001:t0
ngr(i)=0;
R(i)=.548*(G*Q^3/mu)^(1/9)*t^(4/9); %Fracture radius
W0(i)=21*(mu^2*Q^3/G^2)^(1/9)*t^(1/9); %Maximum fracture opening width
Pw=Zi-5/(4*pi)*(G*W0(i)/R(i))*log(rw/R(i)); %wellbore net pressure
Pwi(i)=Pw;
time(i)=t;
i=i+1;
end
figure(30)
set(30,'name','P3D frac growth-(R vs t) (W vs t)','numbertitle','off')
drawnow;
limitRi=.548*(G*Q^3/mu)^(1/9)*tf^(4/9); %used for axis limits
limitW0=21*(mu^2*Q^3/G^2)^(1/9)*tf^(1/9);
subplot(221)
ezplot(sprintf('z.^2/%f +x.^2/%f -1',(h/2)^2,(R(end))^2),[-0 limitRi -h h]);
ylabel('Height')
xlabel('Depth[ft]')
subplot(222)
ezplot(sprintf('z.^2/%f +y.^2/%f -1',(h/2)^2,(W0(end)/2)^2),[-limitW0 limitW0 -h h]);
ylabel('Heigth[ft]')
xlabel('Width[in]')
daspect([12,1,1]);
set(gca,'xtick',[])
subplot(224)
hold;
A=R(end);B=W0(end)/2;C=h/2;
tp = linspace(0,2*pi,100);
pp = linspace(0,pi,100);
[T,P] = meshgrid(tp,pp);
x = A*cos(T).*cos(P);
y = B*cos(T).*sin(P);
z = C*sin(T);
surf(x,y,z);
daspect([1,6,1]);
view(-51,22)
xlabel('Depth[ft]');
ylabel('Width[in]');
zlabel('Height[ft]');
axis([0,limitRi,-limitW0,limitW0,-h/2,h/2]);
end
clearvars ngr tp tt T P y z i
tp = linspace(0,2*pi,1000);
pp = linspace(0,pi,1000);
[T,P] = meshgrid(tp,pp);
y = B*cos(T).*sin(P);
z= C*sin(T);
for i=1:length(y)
ngr(i)=0;
end
hold;
plot3(ngr,y,z,'r')
daspect([1,6,1]);
view(-51,22)
[~,h3]=suplabel(sprintf('time = %0.1g min n the 3d frac shape with 1:2 scale n',t0));grid on;
T=time;P=Pwi;
end](https://image.slidesharecdn.com/ef819075-8889-4c09-9d6d-bcf177eabbf7-150903161232-lva1-app6892/85/A-Comparison-Study-of-KGD-PKN-and-a-Modified-P3D-Model-II-7-320.jpg)