A Modular Genetic Algorithm Specialized for Linear Constraints
1 like370 views
This algorithm combines modules and operators of standard GAs with specilized routines aimed at archieving enhanched performance on istances with specific types of constraints, in particular linear.
A Modular Genetic Algorithm Specialized for Linear Constraints
- 1. A Modular Genetic Algorithm Specialized for Linear Constraints Stefano Costanzo, Lorenzo Castelli, Alessandro Turco
- 2. Genetic Algorithms Genetic Algorithms are popular stochastic optimization methods inspired by the evolutionist theory on the origin of species and natural selection. GAs are particularly suitable for solving complex single and multi-objective problems and finding reasonably good trade-off solutions. 2
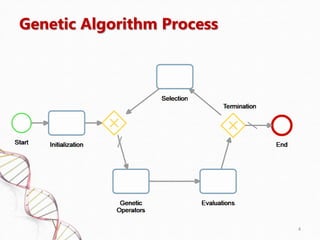
- 3. How it works GAs are designed to simulate processes in natural systems necessary for evolution, following the Survival of the fittest by Charles Darwin. GA initializes a population and improves it through iteration of the selection, genetic operators and evaluation phases. 3
- 5. Target Effectively tackle problems with specific characteristics and maintain at least the performance of state-of-the- art Genetic Algorithms. 5
- 6. Problem characteristics Linear constraints Nonlinear constraints Equality constraints Variable Bounds Single-objective problems Multi-objective problems 6
- 7. Modularity Each phase is well defined and independent New valid phases are simple to design Multiple alternatives can co-exist Wide variety of specialized GA phases in literature 7
- 9. Modularity Exploitation - Selection 9
- 10. Modularity Exploitation Genetic Operators 10
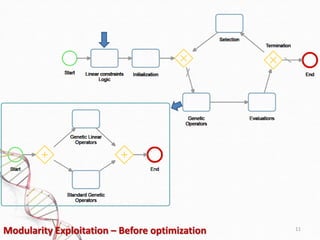
- 11. Modularity Exploitation Before optimization 11
- 12. Before Optimization - Linear Constraints Logic 12
- 14. MOGASI Multi-Objective Genetic Algorithm for Structured Inputs
- 15. MOGASI - Complete Initialization Phase 15
- 16. MOGASI - Main Loop 16
- 17. Benchmarking Three different categories of tests are performed: Constrained single-objective problem Unconstrained multi-objective problem Constrainted multi-objective problem 17
- 18. Benchmarking For each category multiple tests are chosen: Constrained single-objective problem from Michalewicz Library: t01, t02, t06, t12, t13, t17, t26 Unconstrained multi-objective problem from NSGA-II tests: SCH, POL, KUR, ZDT1, ZDT2, ZDT4 Constrained multi-objective problem from NSGA-II tests: DEB, SRN, TNK, WATER 18
- 19. Competitors State of the Art GAs GENOCOP III Non-dominated Sorting Genetic Algorithm, NSGA-II Multi-Objective Genetic Algorithm, MOGA-II Z. Michalewicz and G. Nazhiyath - Genocop III: co-evolutionary algorithm for numerical optimization problems with nonlinear constraints K. Deb A fast and elitist multiobjective genetic algorithm: NSGA-II C. Poloni, V. Pediroda - GA coupled with computationally expensive simulations: tools to improve efficiency 19
- 20. Single Objective Problems Test name t13 Objective Function: Constraint: Bounds: Average Optimal Solution Percentage Deviation GENOCOP 0.1422 % MOGASI 0.0000 % NSGA-II 43.704 % MOGA-II 40.527 % GENOCOP 24.9644 MOGASI 25.0000 NSGA-II 14.0738 MOGA-II 14.8680 10,00 12,00 14,00 16,00 18,00 20,00 22,00 24,00 26,00 Genocop MOGASI NSGA-II MOGA-II 20
- 21. Medal Table Single-Objective Problems 21 1st 2nd 3rd 4th
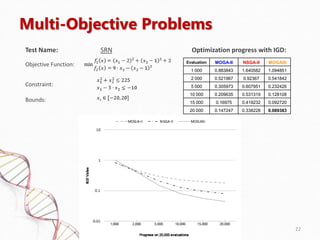
- 22. Multi-Objective Problems Test Name: SRN Optimization progress with IGD: Objective Function: Constraint: Bounds: Evaluation MOGA-II NSGA-II MOGASI 1 000 0.883843 1.640582 1.094851 2 000 0.521967 0.92367 0.541842 5 000 0.305973 0.607951 0.232426 10 000 0.209635 0.531319 0.128108 15 000 0.16975 0.419232 0.092720 20 000 0.147247 0.338228 0.069383 22
- 23. Medal Table - Multi-Objective Problems 23 1st 2nd 3rd
- 24. Conclusions Problem meta-type defined by characteristics Exploited specific characteristics knowledge Kept standard GAs performance Good results in Benchmarks Easy case study expansion 24
- 25. Thank you for your attention