aaa.pptx
Download as PPTX, PDF0 likes19 views
This document discusses circular and rotational motion. It defines rotational motion as motion about an axis and circular motion as the motion of a point on a rotating object. The document provides equations for relating angular quantities like displacement, velocity, and acceleration to linear quantities like arc length and tangential speed/acceleration. It also discusses centripetal force and acceleration. Key scientists who contributed to the understanding of gravitational and planetary motion are mentioned, including Kepler's laws of planetary motion and Newton's universal law of gravitation.
aaa.pptx
- 2. Circular and Rotational Motion
- 3. Rotational motion- motion of a body that spins about an axis Axis of rotation-line about which the rotation occurs A point on a rotating object undergoes circular motion, because a single point always travels in a circle. Arc Length The distance traveled by a point in a time interval (t) moves a distance s.
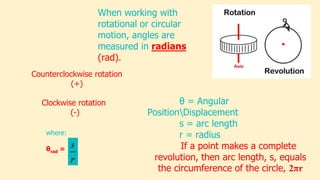
- 4. r s When working with rotational or circular motion, angles are measured in radians (rad). where: 慮rad = 慮 = Angular PositionDisplacement s = arc length r = radius If a point makes a complete revolution, then arc length, s, equals the circumference of the circle, 2r Counterclockwise rotation (+) Clockwise rotation (-)
- 5. The angle for this piece of pie is equal to 1 radian (about 57.3 ). Thus, all three of its sides are of equal length.
- 6. While riding on a carousel that is rotating clockwise, a child travels through an arc length of 11.5m. If the childs angular displacement is 165 degrees, what is the radius of the carousel? Example Angular Position/Displacement deg =-165 s=-11.5m r s 慮rad = 慮rad =s/r r=s/ 慮rad r= -11.5m/-2.88rad r=3.99m
- 7. Describing Angular Motion Previously we used the degree () to measure angles. In most scientific calculations it is the radian (rad) that is used The length of circular arc = radius 1 rev = 360 = 2 rad Conversion 慮rad= 慮deg(/180) 慮deg= 慮rad(180/ )
- 8. Average Angular speed- rate at which a body rotates about an axis t avg = SI units: rad/s or revolutions/s (1 revolution = 2 rad).
- 9. Example: Average Angular Velocity rad = avg = 4.0rad/s t=? t avg = t=6.28s How many revolutions? 4.0 revolutions
- 10. Angular acceleration- time rate of change of angular speed; the units are rad per second per second or rad/s2 avg = average angular acceleration. If the object that is rotating is rigid, all points on that object have the same angular speed and acceleration. 1 2 1 2 t t avg= t =
- 11. A cars tire rotates at an initial angular speed of 21.5 rad/s. The driver accelerates, and after 3.5 s, the tires angular speed is 28.0 rad/s. What is the tires average angular acceleration during the 3.5 s time interval? Ex: Angular Acceleration 1 2 1 2 t t avg= =28.0 rad/s -21.5 rad/s 3.5s = 1.86rad/s2
- 12. If angular acceleration and angular velocity has the same sign the object is speeding up If angular acceleration and angular velocity have opposite signs the object is slowing down Meaning of the Sign
- 13. vf = vi + at f = i + t x = vit + 1/2at2 = it + 1/2(t)2 vf 2 = vi 2 + 2ax f 2 = i 2 + 2≠ x = 遜 `(vi + vf)t = 遜 (i + f)t Angular Kinematics
- 14. The wheel on an upside down bicycle moves through 11.0 rad in 2.0 s. What is the wheels angular acceleration if its initial angular speed is 2.0 rad? = 11.0 rad t=2.0s i= 2.0 rad/s =? = it + 1/2(t)2 = 2( - it ) t2 = 2(11.0rad-(2.0rad)(2s) = 3.5rad/s2 (2.0s)2 Angular Kinematics Example
- 15. Tangential speed- the instantaneous linear speed of an object directed along the tangent to the objects circular path; also called instantaneous linear speed Tangential speeds differ if the points are different distances from the center of rotation (different radii). Vt=r or Vt= 2r T T=t for one rotation
- 16. The radius of a CD in a computer is 0.0600 m. If a microbe riding on the discs rim has a tangential speed of 1.88 m/s, what is the discs angular speed? r=0.0600m Vt= 1.88m/s =? Vt=r =Vt/r = 1.88m/s = 31.3 rad/s 0.0600m Tangential Speed Example:
- 17. Tangential acceleration: instantaneous linear acceleration of an object directed along the tangent to the objects circular path; acceleration is change in tangential velocity over time. at= r SI units = m/s2
- 18. Tangential Acceleration Example A spinning ride at a carnival has an angular acceleration of 0.50 rad/s2. How far from the center is a rider who has a tangential acceleration of 3.3 m/s? =0.500rad/s2 at= 3.30m/s r =? at= r r = at/ r=3.3m/s2=6.60m 0.50rad/s
- 19. Centripetal Acceleration Centripetal means center seeking Centripetal acceleration acceleration towards the center of circle ac = v2 / r ac = 42r / T2
- 20. Centripetal Acceleration ac = v2 / r ac = 42r / T2 A rubber stopper is attached to a 0.93 m string. The stopper is swung in a horizontal circle, making one revolution in 1.18 s. What is the centripetal acceleration of the stopper? A runner moving at a speed of 8.8 m/s rounds a bend with a radius of 25 m. What is the centripetal acceleration of the runner?
- 21. Centripetal Force Centripetal Force Force that is directed towards the center of circle that allows an object to follow a circular path Fc = m ac An athlete whirls a 7 kg hammer tied to the end of a 1.3 m chain. The hammer makes one revolution in 1.0 s. What is the centripetal acceleration of the hammer? What is the tension in the chain?
- 22. Key Scientists and Developments 1543 Copernicus publishes his theory that the solar system is heliocentric (sun centered). He believes the orbits are circular. 1576 Brahe begins meticulously observing and recording planetary motions. He believes the solar system is geocentric (earth centered). 1600 Kepler begins working for Tycho Brahe. After Tychos death, Kepler uses the Tychos data to develop his three laws. ~1600 Galileo proves gravity is uniform (a constant). ~1687 Newton develops the Universal Law of Gravitation. 1798 Cavendish proves the value of G in Newtons Law of Gravitation ~1830 Michael Faraday develops the concept of a field force
- 23. Newtons Universal Law of Gravitation States that the attractive force between two objects is directly proportional to the product of the masses and inversely proportional to the square of the distance between the objects centers.
- 24. Law of Gravitation F = gravitational force G = gravitational constant (6.67 X 10 -11) m = mass of objects d = distance between the two objects F = G (m1) (m2) / d2
- 25. Henry Cavendish found the value of G (Universal Gravitational Constant) G = 6.67 x 10 -11 Nm2/kg2
- 26. Keplers Laws of Planetary Motion 1. The paths of the planets are ellipses with the center of the sun at one focus. 2. An imaginary line from the sun sweeps out equal areas in equal time intervals. Thus, the planets move fastest when closest to the sun.
- 27. Keplers Third Law Tb Ta = 2 ra rb 3 Ta = period of Planet A Tb = period of Planet B ra = Planet As average distance from the sun rb = Planet Bs average distance from the sun 3. Ratio of the squares of the periods of any two planets revolving about the sun is equal to the ratio of the cubes of their average distance from the sun.