![B: 解説
● 文字列が 12 個あることはとりあえず忘れて、
まずは 1 個の文字列に 'r' が入っているか判定
●
言語によって細部は異なるが
おおむねこのようなコードでできる
found = 0 // 文字列 S に 'r' が 入っていれば 1, 入っていなければ 0 に
for i = 0 .. |S|-1 do
if S[i] = 'r' then found = 1
end for
// この時点で found に判定結果が入っている](https://image.slidesharecdn.com/abc029-150919140601-lva1-app6891/85/AtCoder-Beginner-Contest-029-8-320.jpg)
AtCoder Beginner Contest 029 解説
- 1. AtCoder Beginner Contest #029 解説 by @evima0
- 2. 問題 A - 复数形
- 3. A: 問題内容 ● 文字列が入力されるので 「复数形」にして出力してください。 “dog” → “dogs” “chokudai” → “chokudais”
- 4. A: 解説 ● 入出力がわからん！ という人は AtCoder トップページのコレ → を参照 「入力された文字列をそのまま出力」したりする ソースコードがのっています ちょっと書き足して 's' を付け足すようにしましょう
- 6. 問題 B - カキ
- 7. B: 問題内容 ● 12 個の文字列が入力されるので 「牡蠣を食べてもいい月」 ('r' がつく月) の個数を数えてください “September” : 食べていい “August” : 食べちゃダメ
- 8. B: 解説 ● 文字列が 12 個あることはとりあえず忘れて、 まずは 1 個の文字列に 'r' が入っているか判定 ● 言語によって細部は異なるが おおむねこのようなコードでできる found = 0 // 文字列 S に 'r' が 入っていれば 1, 入っていなければ 0 に for i = 0 .. |S|-1 do if S[i] = 'r' then found = 1 end for // この時点で found に判定結果が入っている
- 9. B: 解説 ● 1 個の文字列について判定できたら、 それを 12 回繰り返して結果を集計する ans = 0 // 答えをここに入れる for i = 0 .. 11 do 標準入力から文字列を読み込んで S に入れる （ここに前ページのコード） ans = ans + found end for print ans
- 11. 問題 C - Brute-force Attack
- 12. C: 問題内容 ● 長さ N の文字列で 'a', 'b', 'c' 以外の文字を含まないものを 「辞書順」に列挙してください。 N = 2 → aa, ab, ac, ba, bb, bc, ca, cb, cc ● 1 N 8≦ ≦
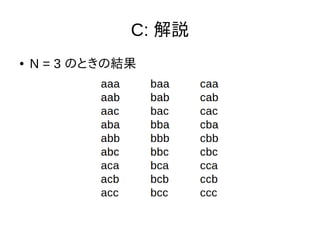
- 14. C: 解説 ● N = 3 のときの結果
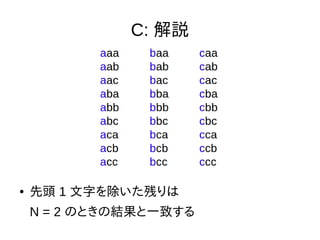
- 15. C: 解説 ● 先頭 1 文字を除いた残りは N = 2 のときの結果と一致する
- 16. C: ソースコード例 (C++) ● ちょっと唐突ですが ここでソースコードを ● N-1 のケースに 帰着させることで 再帰関数を用いて シンプルに書けます ● よく分からなかったら N = 3 のケースを 手で実行してみよう
- 17. 問題 D - 1
- 18. D: 問題内容 ● 1 から N までのすべての整数を 一回ずつ紙に書いたとき 1 という数字は何回書かれるか? ● N = 12 → 5 (1 2 3 4 5 6 7 8 9 10 11 12) ● 20点: 1 N 999≦ ≦ 100点: 1 N < 10≦ 9
- 19. D: 解説 (部分点) ● 1 から 999 くらいなら全部「書け」ます ● 整数を文字列に変換して問題 B と同じ要領で 1 を数える （この方法は言語ごとにかなり異なるので 調べてください） ● 補足: AtCoder で部分点を狙う場合、「正解したいテストケース」 以外が入力されたらすぐに終了するようにすると結果が早く出ます C++ なら #include <cassert> して assert(N <= 999); とか
- 20. D: 解説 (満点) ● 10 億までだと全部「書く」のは 2 秒では厳しい （合計で約 89 億桁、 1 分くらい必要?） ● 「10 には数字の 1 が何個含まれるか?」 「11 には?」「12 には?」という方針から変えよう
- 21. D: 解説 (満点) ● 1 N 999999999:≦ ≦ 各整数は 1 ? 9 桁 ● 9 桁に満たない整数には先頭に 0 を付け足して 9 桁ということにして考えてみる 12345678 → 012345678, 1 → 000000001 ● ついでに、 000000001 から始まるよりは 000000000 から始まったほうがきれい。 1 から N の代わりに、 0 から N の整数について考えることにする （答えは変わらない）
- 22. D: 解説 (満点) 000000000 000000001 : 000000009 000000010 000000011 : 000000020 : 000000099 000000100 : 000002015: N ● 例として N = 2015 のケースを考える ● 先頭の「000000000」も含めて 数字の列が N + 1 = 2016 個ある （左の方の 0 が無駄なようだが、 害はない）
- 23. D: 解説 (満点) 000000000 000000001 : 000000009 000000010 000000011 : 000000020 : 000000099 000000100 : 000002015: N ● まずは 1 の位に注目 01234567890123456789012… 長さ 10 の周期で同じパターンが続く ● N = 2015 の場合、”0123456789” というパターンが 2016 / 10 = 201 回 続き、最後にパターンの先頭から 2016 % 10 = 6 個の数字(“012345”)が並ぶ → 1 という数字は 201 + 1 = 202 個出現する
- 24. D: 解説 (満点) 000000000 000000001 : 000000009 000000010 000000011 : 000000020 : 000000099 000000100 : 000002015: N ● 次に 10 の位に注目 “00000000001111111111222…999” という 長さ 100 の同じパターンが続く ● N = 2015 の場合、パターンが 2016 / 100 = 20 回 続き、最後にパターンの先頭から 2016 % 100 = 16 個の数字 (“0000000000111111”)が並ぶ → 1 という数字は 10 * 20 + 6 = 206 個出現する ● 100 の位以降も同様に計算し、 1 億の位までのすべての位での出現数の総和が答え
- 25. D: ソースコード例 (満点) ● あえて 省略 頑張って実装してください。 一つだけ補足: 今回のように 32bit 整数の上限 (21億+α) 付近の 数を扱う場合、 64bit 整数を使うと安全です。 (今回は 1 N≦ < 109 なのでおそらく大丈夫ですが)