Acceleration Modelling of EV1_FR8695
- 1. Name: Siddhesh Ozarkar MSME Dept. Mechanical Engineering Wayne State University, Detroit P: 313.330.5196 E: fr8695@wayne.edu ACCELERATION MODELLING OF GM EV1 9/14/2015 Acceleration Modelling from 0 to 60mph for GM EV1 Gm Ev1 is a small electric vehicle which has played important role in the recent developments of electric vehicles. This report contains simple calculations to predict the acceleration of EV1 computed from the given data. Simple differential equations solved on MATLAB.
- 2. Acceleration Modelling of GM EV1 Page 1 ---Equation 2 } Acceleration governing equations for mass m= 1560kg ---Equation 1 Acceleration Modelling of GM EV1 A C C E L E R AT I O N M O D E L L I N G F R O M 0 T O 6 0 M P H F O R G M E V 1 Part 1: Acceleration Performance Simulation of EV1 using MATLAB script. Case 1: Mass of vehicle m =1560kg. The acceleration of the vehicle is computed in two phases. Phase one is considered when the torque supplied by the motor linearly increases with speed. This is true for most types of motors that are used to propel electric drive vehicles. The torque of the motor used in ev1 increase linearly till 140 Nm till motor reaches critical speed Žēc. In the later phase this torque reduces in simple relation with velocity & motor operates at constant power of 102kW replicating the WOT conditions. Tmax=140Nm Žēc=733 rad/s Torque is maximum until velocity v=19.8m/s (v=71.3km/h) As velocity reaches 19.8m/s the motor operates at constant power this is the condition of WOT test T = 10200 37 ŌłŚ v For initial phase of acceleration when T=Tmax Case: Now considering mass of the vehicle with two passengers each weighing 70 kg we have the overall mass of the vehicle as 1560kg. Now substituting the values of constants from table 1 in the Equation 2 & considering Equation 1 Phase 1 of Acceleration: 3.117-0.000136v2=( ØææØæŻ ØææØæĪ ) Phase 2 of acceleration: 62.1 ØæŻ -0.046-0.000136v2
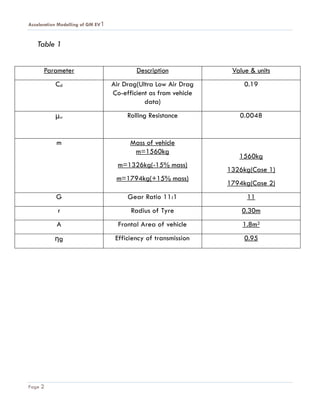
- 3. Acceleration Modelling of GM EV1 Page 2 Table 1 Parameter Description Value & units Cd Air Drag(Ultra Low Air Drag Co-efficient as from vehicle data) 0.19 ╬╝rr Rolling Resistance 0.0048 m Mass of vehicle m=1560kg m=1326kg(-15% mass) m=1794kg(+15% mass) 1560kg 1326kg(Case 1) 1794kg(Case 2) G Gear Ratio 11:1 11 r Radius of Tyre 0.30m A Frontal Area of vehicle 1.8m2 ╬Ęg Efficiency of transmission 0.95
- 4. Acceleration Modelling of GM EV1 Page 3 Description of Graph 1 At 60Mph the time required to reach the speed is 9.1 seconds. The values of acceleration are respectable. The velocity is observed to be constant 128kmph. MATLAB script for obtaining acceleration m=1560kg: % Acceleration Performance simulation of GM EV1 t=linspace(0,15,151); % time from 0 to 15 seconds with 0.1 second timestep v=zeros(1,151); % 150 readings of velocity dT=0.1; %0.1second time step for n=1:150 if v(n)<19.8 v(n+1)=v(n)+dT*(3.107-(0.000136*(v(n)^2))); elseif v(n)>35.8 v(n+1)=v(n); else v(n+1)=v(n)+dT*((62.1/v(n))-0.046-(0.000137*(v(n)^2))); end; end; v=v.*3.6; plot(t,v); xlabel('Time/second'); ylabel('velocity/kph'); title('Acceleration Simulation of GM EV1'); legend('Acceleration of EV1','Location','northwest'); Results for the Case: Graph 1
- 5. Acceleration Modelling of GM EV1 Page 4 } Acceleration governing equations for mass m= 1326kg Part 2: Acceleration Performance Simulation of EV1 using MATLAB script with reduced and increase overall mass of the vehicle. Case 1: Mass of vehicle m =1326kg. Case: Now considering mass of the vehicle with two passengers each weighing 70 kg we have the overall mass of the vehicle as 1326kg. Now substituting the values of constants from table 1 in the Equation 2 & considering Equation 1. Phase 1 of Acceleration: 3.6641-0.0001606v2=( ØææØæŻ ØææØæĪ ) Phase 2 of acceleration: 73.05 ØæŻ -0.047-0.0001606v2 MATLAB script for obtaining acceleration m=1326kg: % Acceleration Performance simulation of GM EV1 t=linspace(0,15,151); % time from 0 to 15 seconds with 0.1 second timestep v=zeros(1,151); % 150 readings of velocity dT=0.1; %0.1second time step for n=1:150 if v(n)<19.8 v(n+1)=v(n)+dT*(3.6641-(0.0001606*(v(n)^2))); elseif v(n)>35.8 v(n+1)=v(n); else v(n+1)=v(n)+dT*((73.05/v(n))-0.0470-(0.0001606*(v(n)^2))); end; end; v=v.*3.6; plot(t,v); xlabel('Time/second'); ylabel('velocity/kph'); title('Acceleration Simulation of GM EV1'); legend('Acceleration of EV1','Location','northwest');
- 6. Acceleration Modelling of GM EV1 Page 5 Description of Graph 2 At 60Mph the time required to reach the speed is 7.8 seconds. The values of acceleration are respectable. The velocity is observed to be constant 128kmph. It can be observed that the acceleration of the vehicle is quicker and the the vehicle approaches the 60mph mark nearly 2 seconds quicker if mass is reduced by 15%. This is simply governed by NewtonŌĆÖs Law F=ma M=mass & a=acceleration Results for Case 1: Graph 2
- 7. Acceleration Modelling of GM EV1 Page 6 } Acceleration governing equations for mass m= 1794kg Case 1: Mass of vehicle m =1794kg. Case: Now considering mass of the vehicle with two passengers each weighing 70 kg we have the overall mass of the vehicle as 1794kg. Now substituting the values of constants from table 1 in the Equation 2 & considering Equation 1. Phase 1 of Acceleration: 2.696-0.000118v2=( ØææØæŻ ØææØæĪ ) Phase 2 of acceleration: 53.998 ØæŻ -0.047-0.000118v2 MATLAB script for obtaining acceleration m=1794kg: % Acceleration Performance simulation of GM EV1 t=linspace(0,15,151); % time from 0 to 15 seconds with 0.1 second timestep v=zeros(1,151); % 150 readings of velocity dT=0.1; %0.1second time step for n=1:150 if v(n)<19.8 v(n+1)=v(n)+dT*(2.696-(0.00011872*(v(n)^2))); elseif v(n)>35.8 v(n+1)=v(n); else v(n+1)=v(n)+dT*((53.998/v(n))-0.04708-(0.0001187*(v(n)^2))); end; end; v=v.*3.6; plot(t,v); xlabel('Time/second'); ylabel('velocity/kph'); title('Acceleration Simulation of GM EV1'); legend('Acceleration of EV1','Location','northwest');
- 8. Acceleration Modelling of GM EV1 Page 7 Description of Graph 3 At 60Mph the time required to reach the speed is 10.5 seconds. The values of acceleration are respectable. The velocity is observed to be constant 128kmph. It can be observed that the acceleration of the vehicle is slower and the vehicle approaches the 60mph mark nearly 1.5 seconds later if mass is increased by 15%. This is simply governed by NewtonŌĆÖs Law F=ma M=mass & a=acceleration Results for Case 1: Graph 3
- 9. Acceleration Modelling of GM EV1 Page 8 Discussion & Comparison: Mass of Vehicle (kg) Time required to reach the 60mph mark (Seconds) 1560 9.1 1326 (-15%) 7.8 1794 (+15%) 10.5 It can be observed from the graphs obtained the effect of mass on the acceleration of the vehicle. As mass increases the acceleration decreases and vice versa. Part 3: Mathematical solution to find out velocity solution using Calculus. **For this part of the report I have considered the governing acceleration for phase 1 when vehicle weighs 1560kg. The reduced differential equation for the acceleration is as follows 3.117-0.000136v2=( ØææØæŻ ØææØæĪ ) where, v= velocity in m/s ’éĘ This is a First Order Non-linear Ordinary Differential Equation. ’éĘ The eqution can be reduced in an alternative form as VŌĆÖ(t)=-0.00013(v(t)-154.6)(v(t)+154.6) ’éĘ Initial conditions as v (t)=0 when t=0 seconds ’éĘ On solving we get the solution to differential equation as V (t) =154.67*( ØæÆ0.0402ŌłŚØæĪŌłÆ2.71824021.44ØÉČ 2.71824021.44ØæÉ+ØæÆ0.0402ØæĪ ) where C = constant of integration.
- 10. Acceleration Modelling of GM EV1 Page 9 The verification from MATLAB shows that velocity at 7 seconds is 77.57km/h. The difference in MATLAB and hand calculation using calculus might be due to the number of decimals that MATLAB uses during computation. The verification from MATLAB shows that velocity at 9.1 seconds is 96.17 km/h. Verification of Solution: 1. Velocity when time t=7 seconds Using calculus and the solution for the differential equation we get ’éĘ v(7) = 21.61m/s = 77.79 km/h 2. Velocity when time t = 9.1 seconds ’éĘ V(9.1) = 27.9m/s = 97.2 km/h
- 11. Acceleration Modelling of GM EV1 Page 10 The verification from MATLAB shows that velocity at 5 seconds is 55.79 km/h. 3. Velocity when time t = 5 seconds ’éĘ v(5)= 15.49 m/s = 55.77 km/h Similar hand calculations can be performed for the phase two of the acceleration and the obtained first order nonlinear differential equation can be solved accordingly Conclusion: ’éĘ The curve obtained in graph 1 closely resembles the curve obtained from the manufactures data. ’éĘ The acceleration of the vehicle reduces as the mass increases as expected. ’éĘ The hand calculations done closely match the calculations done by MATLAB. ’éĘ There is a slight difference in the values of velocity obtained from hand calculations and MATLAB this might be due to the way matlab handles the decimal numbers. References: J.Y. Wong ŌĆ£Theory of ground Vehicles 3rd editionŌĆØ Larminie & Lowry, ŌĆ£Electric Vehicle Technology Explained, 2nd ed.ŌĆØ 2012