AI Unit-3(Ch-6_CSP) Constraint satisfaction problem.pptx
- 1. Unit-3 Constraint Satisfaction Problems Chapter 6 Book: Artificial Intelligence (Stuart Russel and Peter Norvig) 4th edition Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 2. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Introduction to CSP ? CSP is defined by a set of variables, X1, X2, ....Xn, and a set of constraints C1, C2,...Cm. ? Each variable Xi has a non-empty domain Di of possible values. ? Each constraint Ci involves some subset of the variables and specifies the allowable combination of values for that subset. ? A state of the problem is defined by an assignment of values to some or all of the variables, {Xi=vi, Xj=vj,...}
- 3. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Introduction to CSP (terminology) ? An assignment that does not violate any constraint is called a consistent or a legal assignment. ? A complete assignment is one in which every variable is mentioned and a solution to CSP is a complete assignment that satisfies all the constraints. ? Some CSPs also require a solution that maximizes the objective function. ? Constraint satisfaction problems (CSPs) consist of variables with constraints on them. The structure of a CSP can be represented by a constraint graph.
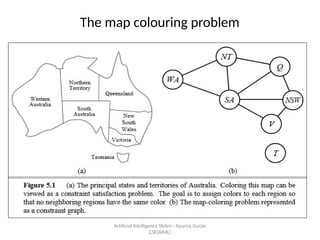
- 4. The map colouring problem Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 5. The map colouring problem as a CSP Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 6. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Varied types of problems as a CSP ? Many kinds of design and scheduling problems can be expressed as CSPs, so they form a very important subclass. CSPs can be solved by general-purpose search algorithms, but because of their special structure, algorithms designed specifically for CSPs generally perform much better. ? For example, the 8-queens problem can be viewed as a CSP in which the variables are the locations of each of the eight queens; the possible values are squares on the board; and the constraints state that no two queens can be in the same row, column or diagonal. ? A solution to a CSP specifies values for all the variables such that the constraints are satisfied. ? Cryptarithmetic and VLSI layout can also be described as CSPs .
- 7. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Approaches to solving CSPs ? Every solution of CSP must be a complete assignment and therefore appears at depth n, if there are n variables. The search tree also extends till depth n. ? Therefore, depth first search algorithms are popular for solving CSPs. ? Moreover, the path by which the solution is reached is irrelevant. Due to this local search methods are also suitable for solving CSPs. These methods use complete-state formulation in which every state is a complete assignment that might or might not satisfy the constraints.
- 8. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) CSP variables, domains and constraints ? CSP variables can be discrete and have finite domains. ¨C Map coloring problems ? If the maximum domain size of any variable is d, then the number of possible complete assignments is O(dn). Here n is the number of variables ? Finite domain CSPs include Boolean CSPs, whose variables can be either true or false. ? Discrete variables can also have infinite domains. ¨C Set of integers ¨C infinite domains require a constraint language to describe constraints
- 9. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Type of constraints ? Unary constraints: They restrict the value of a single variable ? Binary constraints: They relate two variables ¨C WA ¡Ù NT ? Higher order constraints involves three or more variables.
- 10. A cryptarithmetic problem ? Each letter stands for a distinct digit. ? The aim is to find a substitution of digits for letters such that the resulting sum is arithmetically correct. ? No leading zeros are allowed. ¨C a) Puzzle b) Constraint Graph for the puzzle Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 11. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Solving cryptarithmetic puzzle as a CSP TWO + TWO = FOUR ? Identifying the variables and domain Variables: T, W, O, F, U, R, These variables belong to the domain {0,1,2,3,4,5,6,7,8,9} ? Identifying the constraints: ¨C F ¡Ù T, F ¡Ù W and so on (for all variables) ¨C Addition constraints on the four columns: ? O+O=R+10*X1 ? X1+W+W=U+10*X2 ? X2+T+T=O+10*X3 ? X3=F ? X1,X2,X3 are auxiliary variables representing the digits(0 or 1, carried over to the next column)
- 12. Cryptarithmetic Solution X3 can be (0,1), leading digits cannot be zero, so X3=1, and hence F=1. X2+T+T=O+10*X3, X3=1, X2=(0,1), assume X2=0 for some solution Therefore T+T=O+10. Starting from T=(0,1,¡.9), T=1,2,3,4 not possible, 5 not possible as O will be zero and O+O=R is violated. Therefore legal values of T= [6,7,8,9] Let T=6, O=2, O+O=2+2=4, therefore R=4, so X1=0, and X2=0 (already assumed), so W can take the values (1,2,3,4) only. But F=1, O=2, T=6(As W+W=U, 3+3=6, so U=6 not possible, so W=3 not possible), R=4. Thus, W cannot take the values (1,2,3,4), so no legal values available hence backtrack to T=6 and choose a new value for T, choose T=7 Therefore 7+7=O+10, O=4, O+O=R+10*X1, so X1=0 and R=8, W=3, U=6 Thus, all variables are assigned, and all constraints are satisfied. Solution: T=7, W=3, O=4, F=1, U=6, R=8, 7 3 4 7 3 4 1 4 6 8 Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 13. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Backtracking search for CSPs ? Backtracking search is a kind of depth first search which is commonly used for solving CSPs. ? It chooses values for one variable at a time and backtracks when a variable has no legal values left to assign. ? Plain backtracking is an uninformed algorithm. ? The search efficiency of the Backtracking search can be improved by ordering of variables as well as ordering of variable values in a specific way. ? This is called variable and value ordering in CSPs. It acts as a kind of heuristics.
- 14. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Backtracking search for CSPs (with heuristics) ? The minimum remaining values and degree heuristics are methods for deciding which variable to choose next in a backtracking search. ? The least constraining value heuristic helps in ordering the variable values.
- 15. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Variable ordering (MRV) Minimum remaining value (MRV)heuristic: It is also called most constrained variable or fail first heuristic. MRV chooses the variable with the fewest legal values. It is called Fail first as it picks a variable that is most likely to cause a failure. Advantages: ¨C It prunes the search tree. ¨C If there is some variable X with zero legal values remaining, MRV will pick it first and failure will be detected immediately. This avoids pointless search through other variables, as the search s bound to be a failure later-on when X is selected.
- 16. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Variable ordering (degree heuristics) ? The degree heuristics attempts to reduce the branching factor by selecting the variable that is involved in largest number of constraints on other unassigned variables. ? In the map coloring algorithm, the degree of SA is 5 (highest). Once SA is chosen by applying degree heuristics, the problem can be solved without any false steps and arrive at a solution without back tracking.
- 17. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Least constraining value heuristic(value ordering) ? Once a variable has been selected, the algorithm must decide on the order in which the values should be examined. ? Least constraining value (LCV) heuristic prefers that value of the variable which does not reduce the choices of other constrained variables. ? For example: let the partial assignment be {WA=red, NSW=green}, next choice is to be done for variable Q. If Q is assigned blue, it would be a bad choice as it eliminates the last legal value left for SA (SA cannot be red or green). The LCV therefore prefers red instead of blue.
- 18. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Propagating information through constraints ? If some constraints are looked at earlier in the space search, then it can reduce the search considerably. ? This can be done by forward checking process. ? Whenever a variable X is assigned, the forward checking process looks at each unassigned variable Y that is connected to X by a constraint. It deletes from Y¡¯s domain, any value that is inconsistent with the value chosen for X. ? The forward checking can detect that the partial assignment done till now is inconsistent.
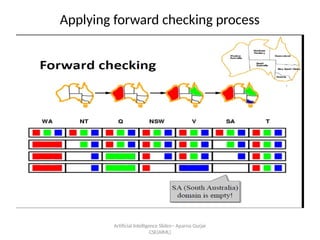
- 19. Applying forward checking process Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 20. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Forward checking process ? Consider the color assignment sequence as WA, Q, V, NT. ? After assigning WA = red and Q = green, and V= blue,the domains of NT and SA are reduced to a single value; the branching on these variables has been eliminated altogether by propagating information from WA and Q. ? The MRV heuristic, which is used for forward checking, would automatically select SA and NT next. ? A second point to notice is that, after V = blue, the domain of SA is empty. Hence, forward checking has detected that the partial assignment { WA = red, Q = green, V = blue) is inconsistent with the constraints of the problem, and the algorithm will therefore backtrack immediately.
- 21. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Intelligent Backtracking Search for CSP Intelligent backtracking: looking backwards ? In simple backtracking, when a branch of search fails, the algorithm backs up to the preceding variable and try a different value for it. This is called chronological backtracking. ¨C Backtracking goes back one level in the search tree at a time. ¨C Not rational in cases where the previous step is not involved with the conflict ? Consider fixed variable ordering Q, NSW, V, T, SA, WA, NT. Suppose partial assignment is as follows: ? {Q= red, NSW= green, V= blue, T=red} ? When next variable SA is taken up for assignment, no valid colour is available(). Backtracking to T does not help as T¡¯s value does not affect other nodes¡¯ constraint.
- 22. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Backjumping ? Backtracking needs to be done till one arrives at a set of variables from which one variable caused the failure. This set is called the conflict set. In this case conflict set is {Q, NSW, V}. ? Definition: Conflict set for a variable X is the set of previously assigned variables that are connected to X by constraints. ? The backjumping method backtracks to the most recent variables in the conflict set. ? In this case backjumping jumps over T and tries a new value for V.
- 23. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Backjumping contd.. ? To enable backjumping the conflict set needs to be maintained while checking for a legal value to assign. If no legal value is found the most recent element of the conflict set is returned with failure indicator. ? Simple backjumping detects when every value in domain is in conflict with current assignment. But if forward checking mechanism is used then such a state is never reached at all. Every branch pruned by basic backjumping is also pruned by forward checking ? Due to this simple backjumping becomes redundant. Therefore conflict-directed backjumping is preferred.
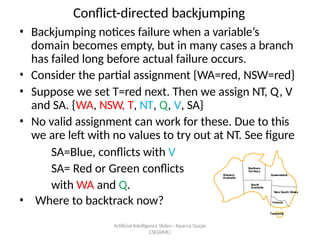
- 24. Conflict-directed backjumping ? Backjumping notices failure when a variable¡¯s domain becomes empty, but in many cases a branch has failed long before actual failure occurs. ? Consider the partial assignment {WA=red, NSW=red} ? Suppose we set T=red next. Then we assign NT, Q, V and SA. {WA, NSW, T, NT, Q, V, SA} ? No valid assignment can work for these. Due to this we are left with no values to try out at NT. See figure SA=Blue, conflicts with V SA= Red or Green conflicts with WA and Q. ? Where to backtrack now? Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)
- 25. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) Conflict-directed backjumping (CBJ) contd.. ? It is a fact that NT, Q, V, SA, taken together, failed because of a set of preceding variables. These must be the variables that directly conflict with the variables NT, Q, V, SA. ? Deeper notion of conflict set: It is the set of preceding variables (WA and NSW) that caused NT, together with any subsequent variables, to have no consistent solution. As per CBJ the conflict set is {WA and NSW}. The algorithm should backtrack to NSW (as it is recent) and skip over Tasmania (T). ? A back-jumping algorithm that uses conflict sets in this way is called as conflict-directed backjumping.
- 26. Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML) CBJ definition ? Conflict-directed backjumping (CBJ): ¨C Let Xj be the current variable, and conf(Xj) its conflict set. If every possible value for Xj fails, backjump to the most recently assigned variable in conf(Xj), denoted by Xi. ¨C Set conflict set of Xi to conf(Xi) = conf(Xi) ? conf(Xj) ¨C {Xi} ¨C If we need to backjump process. View example in next slide from Xi, repeat this
- 27. Conflict-directed backjumping example SA fails, SA conflict set is {WA, NT, Q}, we back-jump to Q and Q absorbs the conflict set from SA into its own conflict set. Q conflict set is {NT, NSW}. Q absorbs the conflict set from SA minus itself. {WA, NT, Q} U {NT, NSW} ¨C {Q}. The new conflict set of Q is {WA, NT, NSW} and so on. Now Q fails(as there is no solution from Q onwards), therefore backjump to NT (which is most recent in Q¡¯s conflict set). NT absorbs {WA, NT, NSW} from Q. Its own conflict set is {WA}. {WA} U {WA, NT, NSW} ¨C {NT}. The new conflict set of NT becomes {WA, NSW}. NT still fails, back-jump to NSW (which is most recent in NT¡¯s conflict set). Thus, from SA the algorithm finally backtracks to NSW, skipping over Tasmania (T). {WA, NSW, T, NT, Q, V, SA} Artificial Intelligence ºİºİߣs-- Aparna Gurjar CSE(AIML)










![Cryptarithmetic Solution
X3 can be (0,1), leading digits cannot be zero, so X3=1, and hence F=1.
X2+T+T=O+10*X3, X3=1, X2=(0,1), assume X2=0 for some solution
Therefore T+T=O+10.
Starting from T=(0,1,¡.9), T=1,2,3,4 not possible, 5 not possible as O
will be
zero and O+O=R is violated. Therefore legal values of T= [6,7,8,9]
Let T=6, O=2, O+O=2+2=4, therefore R=4, so X1=0, and X2=0 (already
assumed), so W can take the values (1,2,3,4) only.
But F=1, O=2, T=6(As W+W=U, 3+3=6, so U=6 not possible, so W=3
not
possible), R=4.
Thus, W cannot take the values (1,2,3,4), so no legal values available hence
backtrack to T=6 and choose a new value for T, choose T=7
Therefore 7+7=O+10, O=4, O+O=R+10*X1, so X1=0 and R=8, W=3, U=6
Thus, all variables are assigned, and all constraints are satisfied.
Solution: T=7, W=3, O=4, F=1, U=6, R=8,
7 3 4
7 3 4
1 4 6 8
Artificial Intelligence ºİºİߣs-- Aparna Gurjar
CSE(AIML)](https://image.slidesharecdn.com/aiunit-3ch-6csp-250313175347-38ba2d4c/85/AI-Unit-3-Ch-6_CSP-Constraint-satisfaction-problem-pptx-12-320.jpg)