AITEES2022-020 - continuous time system PPT.pptx
- 1. Artificial Intelligence Techniques for Electrical Engineering Systems AITEES-2022 Order Reduction of Continuous Time Linear Interval Systems Using Whale Optimization Algorithm (AITEES2022-020) G Ramesh Assistant Professor, Department of EEE, Gudlavalleru M. Siva Kumar Professor, Department of EEE, Gudlavalleru B. Dasu Associate Professor, Department of EEE, Gudlavalleru R. Srinivasa Rao Professor, JNTUK, Kakinada AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru International Conference on
- 2. Contents: ŌĆó Abstract ŌĆó Introduction ŌĆó Problem statement ŌĆó Implementation of WOA ŌĆó Application of proposed method ŌĆó Comparison with other method ŌĆó Conclusion ŌĆó References 2 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 3. Abstract: ’āś This paper presents nature-inspired meta-heuristic optimization algorithm, called Whale Optimization Algorithm (WOA), which mimics the social behaviour of humpback whales. The algorithm has inspired by the bubble-net hunting strategy. ’āś In this paper, WOA has been used for getting Reduced Order Interval Model (ROIM) from higher order linear continuous time interval system. ’āś In this proposed method, the reduced order model denominator and numerator polynomials are obtained based on minimization of cost function of Integral Squared Error (ISE) by using WOA. ’āś Optimization results proved that the WOA algorithm is very competitive compared to the state-of-art meta-heuristic algorithms as well as conventional methods. ’āś The WOA has found to be simple, easy in implementation and provides the optimal solution. 3 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 4. Introduction: ’āś Scientists and engineers have often confronted with the analysis, design and synthesis of real world problems. The first step in such studies is that development of a 'mathematical model' which could be a substitute for the real life problem. ’āś Whenever a physical system has represented by a mathematical model it may yield a transfer function of very high order. ’āś The analysis of higher order system has one of the most important subjects. ’āś Available methods for analysis and design may become cumbersome when applied to a system of higher order. ’āś At this juncture, application of order reduction methods has inevitable to have less computational effort and process time. Since recent years much research work has been reported in international literature. 4 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 5. Introduction: ’āś Most of the industrial processes can be modeled as Linear Time Invariant (LTI) systems, in spite of this fact, that their real behavior of the processes has oftentimes different, much more complicated. ’āś The motivation is evident ŌĆō owing to this, the transfer functions can be used for description of such systems and subsequently also the control theory of linear systems, which is very well-developed, can be applied. ’āś However, an effort to create the simple enough model almost always leads to the origin of uncertainty. Their emergence often consists in neglect of ŌĆ£less important propertiesŌĆØ, especially from the realms of fast dynamic effects, nonlinearities or time-variant behaviors of the plant. 5 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 6. Introduction: ’āś Approximation of higher order systems to lower order models facilitates simulation and design over the complex models. ’āś There has been a tremendous growth in the research area of model order reduction methods, resulting in a development of variety of techniques. ’āś Also, engineering and science designs involve uncertainty specified in a number of ways, as convex or fuzzy descriptions to varying degree, inclining a must study to estimate the upper and lower bounds of the systems for the proper examination. ’āś So, systems with constant coefficients but uncertain within finite range, is classified under interval systems. ’āś Over the years, analysis, stability and transient behavior of interval systems have attracted the attention of researchers. 6 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 7. Problem statement: ’āś Consider an asymptotically stable higher order interval system as: ŌĆ”ŌĆ”.(1) ’āś Where and are lower and upper bounds for numerator and denominator interval polynomial parameters respectively. ’āś It is required to obtain kth Reduced Order Interval Model (ROIM) Rk( s, u, v) using the proposed reduction procedure, defined as: ŌĆ”ŌĆ”.(2) ’āś It is desired to reduce order of the system represented in (1) into (2). 7 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 8. Problem statement: ’āś The Higher Order Interval System represented in equation (1) can be represented as four fixed parameter KharitonovŌĆÖs transfer functions [10]. They are given as: ŌĆ”ŌĆ”.(3) ’āś After obtaining the parameters from the algorithm the Kth order and Ith fixed parameter reduced order model is obtained as follows: ŌĆ”ŌĆ”.(4) ’āś This procedure has applied to all four Kharitonov transfer function and the reduced order interval model has constructed with the coefficients of numerator and denominator polynomials, using the following equation 8 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 9. Implementation of WOA: ’āś Whale Optimization Algorithm (WOA) is a meta-heuristics algorithm. The inspiration for WOA comes from social behavior and the bubble-net hunting of humpback whales in oceans. ’āś The Humpback whales have a one-of-a-kind hunting mechanism known as the bubble-net feeding method. Humpback whales prefer to hunt school of krill or small fishes close to the surface. ’āś The step-wise procedure for the implementation of WOA is given below. ’āś Step1: Exploration Phase (Searching Model): The search agent (humpback whale) looks for the best solution (the prey) randomly based on the position of each agent. Search agent position will be updated during this phase by using a randomly selected search agent rather than the best search agent. 9 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 10. Implementation of WOA: ’āś Step 2: Encircling Prey: Current best candidate solution is assumed to be closes to target prey and other solutions update their position towards the best agent ŌĆ”ŌĆ”.(10) ŌĆ”ŌĆ”.(11) ’āś Step 3: Bubble-net attacking method (exploitation phase): In order to mathematically model the bubble-net behavior of humpback whales, two approaches are follows as: i) Shrinking encircling mechanism: ii) Spiral updating position: ’āś The mathematical model behind the humpback whaleŌĆÖs swimming style around the prey using a shrinking circle and also following a spiral-shaped path at the same time: ’āś ŌĆ”ŌĆ”(12) 10 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 11. Application of proposed method: ’āś Consider an asymptotically stable Higher Order Interval System [4] ’āś Using the procedure given in (3), the four-fixed parameter Kharitonov transfer functions are obtained as follows 11 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 12. Application of proposed method: ’āś The second order reduced models developed by minimizing ISE using reduction technique, is given by ’āś Then the reduced order interval model can be constructed using eq. (5) and is given by 12 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
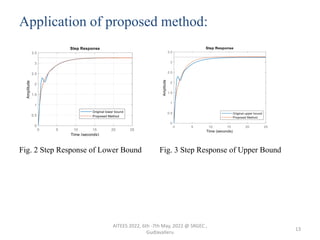
- 13. Application of proposed method: Fig. 2 Step Response of Lower Bound Fig. 3 Step Response of Upper Bound 13 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 14. Comparison with other method : ’āś To show the effectiveness of the proposed method is applied to numerical example and compared with methods [Gamma Delta [2], Mixed Method [3] Mixed Evolutionary Method [5] presented in literature. i) The second order reduced interval model is obtained using Method in [Gamma Delta [2], given by ii) The second order reduced interval model is obtained using Method in [Mixed Method [3], given by iii) The second order reduced interval model is obtained using Method in [Mixed Evolutionary Method [5], given by 14 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 15. Comparison with other method : Fig. 4: Step Response Comparison of Upper Bound Fig. 5: Step Response Comparison of Lower Bound 15 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 16. Conclusion: ’āś In this proposed method, the reduced order interval model denominator and numerator coefficients have been obtained by minimization of a cost function ISE between higher order interval system and reduced order interval model. ’āś It has been observed that the transient and steady state response of reduced order interval model obtained by the proposed method are closely matched. ’āś The proposed method uses a new optimization technique based on nature inspired meta-heuristic from the social behavior and the bubble-net hunting of humpback whales in oceans in solving complex problems. ’āś This method uses single parameter in tuning which in turn reduces computational time hence make it simple and easy in implementation. 16 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 17. References: [1] Vijaya Anand N, Siva Kumar M and Srinivasa Rao R, A novel order reduction procedure for linear time invariant interval systems using SGO algorithm, International Journal of Engineering &Technology, vol.7, no. 8, (2018) 118-122. [2]B Bandyopadhyay, Avinash Upadhye and Osman Ismail (1997), ØøŠ ŌłÆ Øø┐Routh Approximation for Interval Systems, IEEE Trans. On Automatic Control, vol.42, no. 8, pp. 1126-1130. [3] N Selvaganesan (2007), Mixed Method of Model Reduction for Uncertain Systems, Serbian Journal of Electrical Engineering, vol.4, no. 1, pp. 1-12. [4] B. Bandyopadhyay, O. Ismail, and R. Gorez, ŌĆ×Routh Pade Approximation for Interval SystemsŌƤ, IEEE Trans. Autom. Control, 39, 2454ŌĆō2456, 1994. [5] Devender kumar saini and Dr. Rajendra prasad (2010), Mixed evolutionary techniques to reduce order of linear interval systems using generlized routh array, International Journal of Engineering science and technology, vol. 2, no. 10, pp. 5197-5205. [6] B. Bandyopadhyay, ╬│-╬┤ Routh Approximations for Interval SystemsŌƤ, IEEE Trans. Autom. Control, 42, 1127-1130, 1997. [7] Y. Dolgin, and E. Zeheb, ŌĆ×On Routh Pade Model Reduction of Interval SystemsŌƤ, IEEE Trans. Autom. Control, 48 (9), 1610ŌĆō1612, 2003. [8] O. Ismail, and B. Bandyopadhyay, ŌĆ×Model Order Reduction of Linear Interval Systems Using Pade ApproximationŌƤ, IEEE International symposium on circuit and systems, 1995. 17 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru
- 18. Thank you 18 AITEES 2022, 6th -7th May, 2022 @ SRGEC , Gudlavalleru







![Problem statement:
’āś The Higher Order Interval System represented in equation (1) can be
represented as four fixed parameter KharitonovŌĆÖs transfer functions [10].
They are given as:
ŌĆ”ŌĆ”.(3)
’āś After obtaining the parameters from the algorithm the Kth order and Ith
fixed parameter reduced order model is obtained as follows:
ŌĆ”ŌĆ”.(4)
’āś This procedure has applied to all four Kharitonov transfer function and the
reduced order interval model has constructed with the coefficients of
numerator and denominator polynomials, using the following equation
8
AITEES 2022, 6th -7th May, 2022 @ SRGEC ,
Gudlavalleru](https://image.slidesharecdn.com/aitees2022-020ppt-240726170621-945321cf/85/AITEES2022-020-continuous-time-system-PPT-pptx-8-320.jpg)


![Application of proposed method:
’āś Consider an asymptotically stable Higher Order Interval System [4]
’āś Using the procedure given in (3), the four-fixed parameter
Kharitonov transfer functions are obtained as follows
11
AITEES 2022, 6th -7th May, 2022 @ SRGEC ,
Gudlavalleru](https://image.slidesharecdn.com/aitees2022-020ppt-240726170621-945321cf/85/AITEES2022-020-continuous-time-system-PPT-pptx-11-320.jpg)

![Comparison with other method :
’āś To show the effectiveness of the proposed method is applied to
numerical example and compared with methods [Gamma Delta [2],
Mixed Method [3] Mixed Evolutionary Method [5] presented in
literature.
i) The second order reduced interval model is obtained using Method in
[Gamma Delta [2], given by
ii) The second order reduced interval model is obtained using Method
in [Mixed Method [3], given by
iii) The second order reduced interval model is obtained using Method
in [Mixed Evolutionary Method [5], given by
14
AITEES 2022, 6th -7th May, 2022 @ SRGEC ,
Gudlavalleru](https://image.slidesharecdn.com/aitees2022-020ppt-240726170621-945321cf/85/AITEES2022-020-continuous-time-system-PPT-pptx-14-320.jpg)


![References:
[1] Vijaya Anand N, Siva Kumar M and Srinivasa Rao R, A novel order reduction procedure
for linear time invariant interval systems using SGO algorithm, International Journal of
Engineering &Technology, vol.7, no. 8, (2018) 118-122.
[2]B Bandyopadhyay, Avinash Upadhye and Osman Ismail (1997), ØøŠ ŌłÆ Øø┐Routh
Approximation for Interval Systems, IEEE Trans. On Automatic Control, vol.42, no. 8,
pp. 1126-1130.
[3] N Selvaganesan (2007), Mixed Method of Model Reduction for Uncertain Systems,
Serbian Journal of Electrical Engineering, vol.4, no. 1, pp. 1-12.
[4] B. Bandyopadhyay, O. Ismail, and R. Gorez, ŌĆ×Routh Pade Approximation for Interval
SystemsŌƤ, IEEE Trans. Autom. Control, 39, 2454ŌĆō2456, 1994.
[5] Devender kumar saini and Dr. Rajendra prasad (2010), Mixed evolutionary techniques to
reduce order of linear interval systems using generlized routh array, International Journal
of Engineering science and technology, vol. 2, no. 10, pp. 5197-5205.
[6] B. Bandyopadhyay, ╬│-╬┤ Routh Approximations for Interval SystemsŌƤ, IEEE Trans.
Autom. Control, 42, 1127-1130, 1997.
[7] Y. Dolgin, and E. Zeheb, ŌĆ×On Routh Pade Model Reduction of Interval SystemsŌƤ, IEEE
Trans. Autom. Control, 48 (9), 1610ŌĆō1612, 2003.
[8] O. Ismail, and B. Bandyopadhyay, ŌĆ×Model Order Reduction of Linear Interval Systems
Using Pade ApproximationŌƤ, IEEE International symposium on circuit and systems,
1995.
17
AITEES 2022, 6th -7th May, 2022 @ SRGEC ,
Gudlavalleru](https://image.slidesharecdn.com/aitees2022-020ppt-240726170621-945321cf/85/AITEES2022-020-continuous-time-system-PPT-pptx-17-320.jpg)
