Analisis regresi memprediksi permintaan ayam
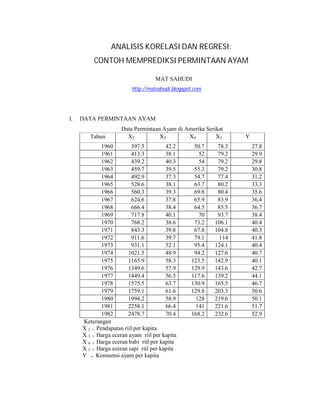
- 1. ANALISIS KORELASI DAN REGRESI: CONTOH MEMPREDIKSI PERMINTAAN AYAM MAT SAHUDI http://matsahudi.blogspot.com I. DATA PERMINTAAN AYAM Data Permintaan Ayam di Amerika Serikat Tahun X2 X3 X4 X5 Y 1960 397.5 42.2 50.7 78.3 27.8 1961 413.3 38.1 52 79.2 29.9 1962 439.2 40.3 54 79.2 29.8 1963 459.7 39.5 55.3 79.2 30.8 1964 492.9 37.3 54.7 77.4 31.2 1965 528.6 38.1 63.7 80.2 33.3 1966 560.3 39.3 69.8 80.4 35.6 1967 624.6 37.8 65.9 83.9 36.4 1968 666.4 38.4 64.5 85.5 36.7 1969 717.8 40.1 70 93.7 38.4 1970 768.2 38.6 73.2 106.1 40.4 1971 843.3 39.8 67.8 104.8 40.3 1972 911.6 39.7 79.1 114 41.8 1973 931.1 52.1 95.4 124.1 40.4 1974 1021.5 48.9 94.2 127.6 40.7 1975 1165.9 58.3 123.5 142.9 40.1 1976 1349.6 57.9 129.9 143.6 42.7 1977 1449.4 56.5 117.6 139.2 44.1 1978 1575.5 63.7 130.9 165.5 46.7 1979 1759.1 61.6 129.8 203.3 50.6 1980 1994.2 58.9 128 219.6 50.1 1981 2258.1 66.4 141 221.6 51.7 1982 2478.7 70.4 168.2 232.6 52.9 Keterangan X 2 = Pendapatan riil per kapita X 3 = Harga eceran ayam riil per kapita X 4 = Harga eceran babi riil per kapita X 5 = Harga eceran sapi riil per kapita Y = Konsumsi ayam per kapita
- 2. Sumber : Gujarati (1995, 228) II. ANALISIS A. Regresi Linier 1. Deskripsi Data Descriptive Statistics Mean Std. Deviation N Y 39.670 7.3730 23 X2 1035.065 617.8470 23 X3 47.996 11.1172 23 X4 90.400 35.2237 23 X5 124.430 51.4997 23 ď‚· Nilai rata-rata hitung dan Std Deviasi variable dependen Y dan varibael independen X2, X3, X4, dan X5 dapat dilihat padat tabel Descriptive Statistics di atas. 2. Korelasi Correlations Y X2 X3 X4 X5 Pearson Y 1.000 .947 .840 .912 .935 Correlation X2 .947 1.000 .932 .957 .986 X3 .840 .932 1.000 .970 .928 X4 .912 .957 .970 1.000 .941 X5 .935 .986 .928 .941 1.000 Sig. (1-tailed) Y . .000 .000 .000 .000 X2 .000 . .000 .000 .000 X3 .000 .000 . .000 .000 X4 .000 .000 .000 . .000 X5 .000 .000 .000 .000 . N Y 23 23 23 23 23 X2 23 23 23 23 23 X3 23 23 23 23 23 X4 23 23 23 23 23 X5 23 23 23 23 23 ď‚· Antara variable Y dan variable-variabel X2, X3, X4, X5 mempunyai korelasi positif yang kuat (> 0,5). 2
- 3. ď‚· Korelasi tertinggi terjadi antara Y dengan X2 (0.947), sementara korelasi terendah terjadi antara Y dengan X3 (0,840) ď‚· Tingkat signifikansi koefisien korelasi satu sisi (Sig. (1-tailed) dari output (diukur dari probabilitas) semuanya menghasilkan 0,000. Oleh karena probabilitas jauh di bawah 0,01 dan 0,05, maka korelasi di antara variable dependen Y dengan variable-variabel independen X2, X3, X4, dan X5 sangat nyata. 3. Adjusted R Square c Model Summary Adjusted R Std. Error of the Model R R Square Square Estimate Durbin-Watson a 1 .971 .943 .930 1.9532 b 2 .969 .939 .930 1.9557 1.252 a. Predictors: (Constant), X5, X3, X4, X2 b. Predictors: (Constant), X5, X3, X4 c. Dependent Variable: Y ď‚· Terdapat dua model regresi linier untuk memprediksi nilai Y dari variable-variabel independen X2, X3, X4, dan X5. ď‚· Model 1: Nilai Y diprediksi dari variable X5, X3, X4, X2. Sementera model 2, nilai Y diprediksi dari variable X5, X3, X4. ď‚· Kedua model itu mempunyai nilai kemampuan memprediksi yang sama (Adjusted R Square), yaitu sebesar 0,930 dan standar error optimasi yang hampir sama. Hal ini berarti bahwa 93% nilai Y, dapat diprediksi dari variable X5, X3, X4, X2 ataupun hanya dari variable variable X5, X3, X4. Perbedaan kedua model prediksi hanya terletak pada Std. Error of the Estimate. 4. ANOVA c ANOVA Model Sum of Squares df Mean Square F Sig. a 1 Regression 1127.259 4 281.815 73.871 .000 Residual 68.670 18 3.815 Total 1195.929 22 b 2 Regression 1123.258 3 374.419 97.893 .000 Residual 72.671 19 3.825 Total 1195.929 22 a. Predictors: (Constant), X5, X3, X4, X2 b. Predictors: (Constant), X5, X3, X4 c. Dependent Variable: Y 3
- 4.  Dari uji ANOVA tampak bahwa kedua model regresi mempunyai nilai signifikansi 0,000. Oleh karena probabiltasnya (0,000) jauh lebih kecil dari 0,05, maka kedua model regresi dapat dipakai untuk memprediksi nilai Y. 5. Koefisien Regresi a Coefficients Standardized Unstandardized Coefficients Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 37.232 3.718 10.015 .000 X2 .005 .005 .420 1.024 .319 X3 -.611 .163 -.922 -3.753 .001 X4 .198 .064 .948 3.114 .006 X5 .070 .051 .485 1.363 .190 2 (Constant) 35.681 3.399 10.496 .000 X3 -.654 .158 -.986 -4.151 .001 X4 .233 .054 1.111 4.275 .000 X5 .115 .024 .806 4.749 .000 a. Dependent Variable: Y  Meskipun kedua model regresi linier dapat digunakan, namun ternyata nilai-nilai koefisien dari variable independen mempunyai nilai yang berbeda.  Pada model 1, tampak bahwa nilai signifikansi koefisien dari variable X2 sebesar 0,319, varibael X4 sebesar 0,006, dan variable X5 sebesar 0, 190. Hal ini menunjukkan bahwa nilai koefisien dari ketiga variable tersebut tidak signifikan, karena lebih besar dari 0,05.  Pada model 2, tampak bahwa semua nilai signifikansi koefisien dari variable X3, X4, X5 bernilai lebih kecil dari 0,05. Hal ini menunjukkan bahwa nilai koefisien dari ketiga variable tersebut bersifat signifikan pada taraf kepercayaan 95%. 6. Persamaan Regresi Linier Berganda Dari analisis-analisis di atas, dapat disimpulkan bahwa nilai Y (Konsumsi ayam per kapita ) di Amerika Serikat dapat diprediksi dari nilai X 3 (Harga eceran ayam riil per kapita), X 4 ( Harga eceran babi riil per kapita), dan X 5 (Harga eceran sapi riil per kapita), dengan persamaan sebagai berikut : Y = 35.681 – 0,654 X 3 + 0,233X 4 + 0,115X 5 4
- 5. Persamaan tersebut dapat menjelaskan variabilitas nilai Y sebesar 93%. Hal ini menunjukkan bahwa konsumsi ayam per kapita di Amerika Serikat 93% dapat dijelaskan dari harga eceran ayam riil per kapita, harga eceran babi riil per kapita, dan harga eceran sapi riil per kapita. Sedangkan 7% konsumsi ayam per kapita di Amerika Serikat dijelaskan oleh variable lain di luar ketiga variable itu. B. Regresi Double Logaritma Regresi ini dilakukan dengan mentransformasi data ke dalam bentuk logaritma alami (ln). Hasil analisis regresinya adalah sebagai berikut: 1. Korelasi Correlations ln y ln x2 ln x3 ln x4 ln x5 Pearson ln y 1.000 .973 .804 .924 .934 Correlation ln x2 .973 1.000 .907 .972 .979 ln x3 .804 .907 1.000 .947 .933 ln x4 .924 .972 .947 1.000 .954 ln x5 .934 .979 .933 .954 1.000 Sig. (1-tailed) ln y . .000 .000 .000 .000 ln x2 .000 . .000 .000 .000 ln x3 .000 .000 . .000 .000 ln x4 .000 .000 .000 . .000 ln x5 .000 .000 .000 .000 . N ln y 23 23 23 23 23 ln x2 23 23 23 23 23 ln x3 23 23 23 23 23 ln x4 23 23 23 23 23 ln x5 23 23 23 23 23 ď‚· Antara variable ln Y dan variable-variabel ln X2, ln X3, ln X4, dan ln X5 mempunyai korelasi positif yang kuat (> 0,5). Korelasi tertinggi terjadi antara ln Y dengan ln X2 (0.973), sementara korelasi terendah terjadi antara ln Y dengan ln X3 (0,804) ď‚· Tingkat signifikansi koefisien korelasi satu sisi (Sig. (1-tailed) dari output (diukur dari probabilitas) semuanya menghasilkan 0,000. Oleh karena probabilitas jauh di bawah 0,01 dan 0,05, maka korelasi di antara variable dependen ln Y dengan variable-variabel independen ln ln X2, ln X3, ln X4, dan ln X5 sangat nyata. 2. Adjusted R Square Model Summary Adjusted R Std. Error of the Model R R Square Square Estimate 1 .991a .982 .978 .02759 b 2 .991 .982 .979 .02746 5
- 6. c 3 .990 .980 .978 .02778 a. Predictors: (Constant), ln x5, ln x3, ln x4, ln x2 b. Predictors: (Constant), ln x3, ln x4, ln x2 c. Predictors: (Constant), ln x3, ln x2 ď‚· Terdapat 3 model regresi ln linier untuk memprediksi nilai ln Y dari variable-variabel independen ln X2, ln X3, ln X4, dan ln X5. ď‚· Ketiga model itu mempunyai nilai kemampuan memprediksi yang hamper sama (Adjusted R Square), yaitu sebesar 0,978 dan standar error optimasi yang hampir sama. Hal ini berarti bahwa 98% nilai ln Y, dapat diprediksi dari variable ln X5, ln X3, ln X4, ln X2 . 3. ANOVA d ANOVA Model Sum of Squares df Mean Square F Sig. a 1 Regression .761 4 .190 249.928 .000 Residual .014 18 .001 Total .775 22 b 2 Regression .760 3 .253 336.181 .000 Residual .014 19 .001 Total .775 22 3 Regression .759 2 .380 491.868 .000c Residual .015 20 .001 Total .775 22 a. Predictors: (Constant), ln x5, ln x3, ln x4, ln x2 b. Predictors: (Constant), ln x3, ln x4, ln x2 c. Predictors: (Constant), ln x3, ln x2 d. Dependent Variable: ln y ď‚· Dari uji ANOVA tampak bahwa ketiga model regresi mempunyai nilai signifikansi 0,000. Oleh karena probabiltasnya (0,000) jauh lebih kecil dari 0,05, maka ketiga model regresi ln linier dapat dipakai untuk memprediksi nilai ln Y. 4. Koefisien Regresi a Coefficients Unstandardized Standardized Coefficients Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 2.190 .156 14.063 .000 ln x2 .343 .083 1.041 4.114 .001 ln x3 -.505 .111 -.596 -4.550 .000 ln x4 .149 .100 .301 1.490 .153 6
- 7. ln x5 .091 .101 .184 .905 .378 2 (Constant) 2.125 .138 15.415 .000 ln x2 .406 .045 1.233 9.063 .000 ln x3 -.439 .083 -.519 -5.266 .000 ln x4 .107 .088 .216 1.214 .240 3 (Constant) 2.033 .116 17.497 .000 ln x2 .452 .025 1.372 18.284 .000 ln x3 -.372 .063 -.440 -5.865 .000 a. Dependent Variable: ln y  Meskipun ketiga model regresi linier dapat digunakan, namun ternyata nilai-nilai koefisien dari variable independen mempunyai nilai signifikansi yang berbeda.  Dari tabel di atas tampak bahwa signifikansi nilai koefisien varibael independen yang keseluruhannya mempunyai nilai 0,00 (kurang dari 0,05) adalah model 3. Hal ini menunjukkan bahwa nilai koefisien dari ketiga variable dari model tersenut bersifat signifikan pada taraf kepercayaan 95% dan 99%. 5. Persamaan Regresi Ln Linier Berganda Dari analisis-analisis di atas, dapat disimpulkan bahwa nilai ln Y (Konsumsi ayam per kapita ) di Amerika Serikat dapat diprediksi dari nilai ln X 3 (Harga eceran ayam riil per kapita), ln X 2 ( pendapatan riil per kapita). Ln Y = 2,033 + 0,452 ln X 2 - 0,372 ln X 3 Persamaan tersebut dapat menjelaskan variabilitas nilai Y sebesar 98%. Hal ini menunjukkan bahwa konsumsi ayam per kapita di Amerika Serikat 98% dapat dijelaskan dari harga eceran ayam riil per kapita dan pendapatan riil per kapita. Sedangkan 2% konsumsi ayam per kapita di Amerika Serikat dijelaskan oleh variable lain di luar kedua variable itu. III. KESIMPULAN Dari analisi di atas, dapat disimpulkan bahwa konsumsi ayam per kapita di Amerika Serikat dijelaskan oleh dua model regresi berganda sebagai berikut. Y = 35.681 – 0,654 X 3 + 0,233X 4 + 0,115X 5 (Adjusted R2 = 0,93) Ln Y = 2,033 + 0,452 ln X 2 - 0,372 ln X 3 (Adjusted R2 = 0,98) Di antara dua model tersebut, model double logaritma lebih baik dari pada model linier karena mempunyai Adjusted R2 yang lebih tinggi. 7