1. Rencana Pelaksanaan Pembelajaran (RPP)
ANALISIS VARIANS
D
I
S
U
S
U
N
Oleh:
Nama : Ida Ayu Siahaan
NPM : 12150011
Mata kuliah ;Statistika
Prodi : Pendidikan Matematika
Dosen Pengasuh : Drs. Hotman Simbolon, MS
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS HKBP NOMMENSEN
PEMATANGSIANTAR
2. Pengertian analisis Varians
Suatu teknik untuk menguji kesamaam beberapa rata-rata
adalah analisis varians. Andaikan ada K perlakuan A1,
A2,, Ai,, Ak yang masing-masing dengan sampel yang
berbeda-beda dengan berturut-turut dengan ukuran atau
banyak pengamatan n1, n2,, ni,,nk maka hipotesis untuk
uji kesamaan rata adalah
Ho: N1=N2=N3==Ni= =Nk
Ha : Paling sedikit dua N tidak sama atau cara penulisannya
lain :
ij,Ni Nj, i j, i, j 1,...,k
3. Analisis Varians tidak hanya digunakan dalam satu jenis
atau factor perlakuan ,tetapi dapat lebih darisatu factor
yang masing-masing factor terdiri dari beberapa
perlakuan. Bila perlakuan terdiri dari satu factor maka
disebut klasiikasi eka arah dan apabila terdiri dari dua
factor disebut klasifikasi dwi arah
4. Dalam analisis varins menyangkut varians dalam
masing-masing perlakuan , varians antar perlakuan, dan
mungkin juga varians interaksi antar perlakuan dari factor
yang satu dengan perlakuan dalam factor yang lain.
Sistem pengujian ntuk klasifikasi eka arah dapat digunakan
menjadi analogi kepada system pengujian untuk dwi arah
atauanalisis varians lannya.
5. Pada umumnya yang menjadi statistika uji adalah uji F
yang di hitung dari perbandingan antar varians yakni
varians antar perlakuan ataupun interaksi terhadap varians
galat.
Sistem pengujian untuk klasifikasi eka arah dapat di
gunakan menjadi analogi kepada sistem pengujian untuk
dwi arah atau analisis varians lainnya
6. Klasifikasi EKA ARAH
Tabel pengamatan K sampel acak
Pelakuan A1 A2 .. Ai .. Ak
Penagamatan X11 X21 .. Xi1 .. Xk1 ..
X12 X22 .. Xi2 .. Xk2
.. .. .. .. .. ..
X1j X2j .. Xij .. Xkj
.. .. .. .. .. ..
X1n X2n .. Xin .. Xkn
Total R1 R2 .. Ri .. Rk R.
Rataan x 1 x 2 .. x i .. x k x
Populasi N1 N2 .. Ni .. Nk N.
7. Masing-masing perlakuan terdiri dari N Pengamatan ,
sehingga semua pengamatan N=nk
Jika penyimpangan pengamatan ke j pada perlakuan ke i
disimbolkan dengan ij dan penyimpangan populasi
perlakuan ke i dari rataan umum ( grad mean = N =裡Ni/k )
adalah i maka pengamatan dapat ditulis ;
Xij =Ni+ij dan Ni=N+ i atau Xij= N+ i +ij dengan
kendala 裡 i=0 dipenuhi karena i=adalah efek atau
pengeruh perlakuan ke i maka hipotesis dapat ditulis
menjadi :
8. H0: 1= 2.....= i= k=0
Ha: Paling sedikit satu i tidak sama dengan 0 atau
penulisan lain
i, i 0
Varians masing-masing perlakuan adalah s2
1 , s2
2 ,., si
2 ,.,sk
2
dimana
1 =
s2
Xij xi
1
1
2
n
n
j
9. sedangkan rataan K varians adalah
Xij Xi
( )
( 1)
Xij
Xi
( 1)
1 1
2
1 1
2
1
2
1
ワ
k
ワ k n
k n
k
i
n
j
k
i
n
j
k
i
s
dinamakan varians dalam perlakuan
k
ワ
i
n
j
Xij Xi
1 1
2 ( ) Jumlah kuadrat dalam perlakuan disingkat JKD
ataupun JKG (jumlah
kuadrat galat) sehingga dapat ditulis :
10. Merupakan salah satu suatu taksiran tak bias untuk
2 .selajutnya telah di ketahui bahwa
n
x
atau 2 =n 2
x
Sedangkan 2
x di duga dengan S 2
x
x x
k
j
i
k
1 1
sehingga
dinamakan varians antar perlakuan =S 2
x
x
k
i
i
k
n
1
2
1
1 n
k n
i x x
i
1
= jumlah kuadrat antar perlakuan dapat S 2
1 =
JKA
K 1
Uji F di cari dengan f =
ians antar perlakuan
var
ians dalam perlakuan
var
11. 2
1
S
S =
F= 2
JKA /( K
1)
adalah peubah acak f dengan derajat
1
JKG K N
kebebasan(K-1) jadi HO ditolak jika
Fh it > Fa : (k-1) Vs k(n-1)
Uji kebebasa klasifikasi ke arah
a H : ....... ........ 0 1 2 3 i k
Ha paling sedikit satu i tidak sama dengan nol atau
penulisan lain
i i, 0
12. Tabel Aalisis Varians untu klasifikasi Eka arah
Sumber
Derajat
Jumlah
Rataan
Variansi
Kebebasan
kwadrat
Kuadrat
F Hit Ho Tolak
Bila F
Hit
Perlakuan K-1 JKA
2
1
S
S >f k-
2
1,k(n-1)
Galat K(n-1) JKG
JKA
JKG
k(n 1)
裡 Kn-1 JKT
1
2
1 K
s
13. Teori Identitas jumlah kuadrat
JKT=JKA+JKG
Bukti:
n
JKT= ワ
j 1
k
i
1
n
( X ij - x ....) 2=ワ
j 1
k
i
1
削
2
..... _ i ij i x x x x
n
=
j
1
k
i
1
( X - x ....) 2+2 ( x x....... x x x x 2
x x
ij ij 1 ij 1 ij i n
=
j 1
k
i 1
n
( X ij - x ....) 2 +2
j 1
k
i 1
i ij i x x ..... _ x x
14. n
+
j
1
k
i 1
( X ij - x ....) 2 ,suku ke dua =0 (buktikan)
n
=
j
1
k
ワ
i 1
n
( X ij - x ....) 2+
j
1
k
ワ
i 1
( X ij - x ....) 2
k
= n ワ
i 1
n
( X ij - x ....) 2+
j
1
k
ワ
i 1
( X ij - x ....) 2
= JKA+ JKG
15. Tabel banyak ikan yang ditangkap dalam 5 menit ( banyak
pengamatan tidak sama )
Jenis umpan
A B C D E F
9 4 2 2 6
8 6 8 3 3 5
8 7 6 7 4 9
9 4 5 5 4
8 2
Total 25 34 23 17 15 20 134
Rataan 8,33 6,8 5,75 4,25 3 6,67 5,58
16. Jawab :
Hipotesis Ho : N1= N2= N3= N4= N5= N6
Ha : i j, Ni Nj, i,j=1,.,6
Taraf signifikasi 0,05 sehingga daerah kritis
F>f0,05 ; 5,18 =2,77
Perhitungan :
JKT = 92+62+82+.+52+92 (1342/ 24) = 125,833
JKA = 252 /3 + 342 /5 + 232 /4 + 172 /4 + 152 /5 + 202 /3
1342 /24
= 74,21
17. JKG = 125,83-74,21 = 51,623
dbA = 5, dbG = 24-6=18
RKA = 74,21/5 = 14,842
RKG = 51,623/18 = 2,868
fhit = 14,842/2,868 = 5,175
Kesimpulan fhit = 5,175>2,77 maka Ho ditolak
Tabel analisis variansnya
Sumber
variansi
Derajat
kebebas
an
Jumla
h
kuadr
at
Rataa
n
kuadr
at Fhit
Ho tolak bila
Fhit
Perlaku
an 5 74,21
14,88
42
5,17
5
>F0,05;5,18
51,62
3 2,868
Galat 18 =2,7
Total 23
125,8
33
18. URAIAN MATERI
8.3.UJI RATAAN KLASIFIKASI DWI ARAH
Tabel pengamatan klasifikasi Dwi arah tanpa interaksi
Faktor 裡 Rataan Populasi
A B1 B2 . Bj . Bb
A1 X11 X12 . X1j . X1b T1 x .1 NA1
A2 X21 X22 . X2j . X2b T2 x .2 NA2
A3 X31 X32 . X3j . X3b T3 x .3 NA3
. . . . . . . . . .
Ai Xi1 Xj2 . Xij . Xib Ti x .i NAi
. . . . . .
Aa Xa1 Xa2 . Xaj . Xab Ta x .a NAa
Total T.1 T.2 . T.j . T.b T..
Rataan x .1 x 2 . x .j . x .b x
Populasi NB1 NB2 . NBj . NBb N
Analisis tanpa interaksi
U.8.4 Analisis varians dwiarah tanpa interaksi
Hipotesis
HoA: NA1=NA2=NA3=.=NAa
HaA: ij, NAi NAj, i j, i,j=1,.,a
HoB: NB1=NB2=NB3=.=NBa
HaB: ij, NBi NBj, i j, i,j=1,.,b
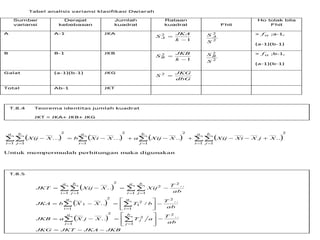
19. Tabel analisis variansi klasifikasi Dwiarah
Sumber
variansi
Derajat
kebebasan
Jumlah
kuadrat
Rataan
kuadrat Fhit
Ho tolak bila
Fhit
A A-1 JKA
JKA
1
2
k
S A
2
S A
2
S
> f ;a-1,
(a-1)(b-1)
B B-1 JKB
JKB
1
2
k
SB
2
S B
2
S
> f ;b-1,
(a-1)(b-1)
Galat (a-1)(b-1) JKG
JKG
dbG
S 2
Total Ab-1 JKT
2
a
T.8.4 Teorema identitas jumlah kuadrat
JKT = JKA+ JKB+ JKG
ワ ... ... .. ワ ..
1
1
2
1
2
1
2
1 1
i
b
j
b
j
a
i
a
i
b
j
Xij X b Xi X a Xij X Xij Xi X j X
Untuk mempermudah perhitungan maka digunakan
T.8.5
ワ ワ
JKG JKT JKA JKB
T
T
T
ab
JKB a X j X T a
ab
JKA b X X T b
ab
JKT Xij X Xij
b
j
j
a
i
a
i
a
i
a
i
b
j
a
i
b
j
..
..
..
.. /
..
..
2
1
2
2
1
2
1
2
1
2
1
1
2
1 1
2
2
1 1
20. Analisis Dwi arah dengan interaksi
Perbedaan dengan tanpa interaksi adalah penambahan analisis efek yang
disebabkan leh kedua factor bersama-sama ( interaksi ). Apakah ada perbedaan efek antara
satu sel dengan sel yang lain misalnya AB11 dengan AB43 dan lain sebagainya
Jadi dalam analisis ini dikenal dua aspek perlakuan
a. Efek Utama ( main Efect ) Khusus antar perlakuan dalam factor A, dan khusus antar
perlakuan dalam factor B.
b. Efek interaksi A dan B
Frekuensi objek dalam sel (n) biasanya disebut replikasi atau ulangan
T.8.6 Teorema identitas jumlah kuadrat
JKT=JKA+JKB+JKAB+JKG
ワワ
X x bn X X an X X
.. .. .. ..
a
b
n
ワワ ワワワ
i
j
k
ijk j
a
i
b
j
ij i j
b
j
j
a
i
i
a
i
b
j
a
k
ijk
n X X X X X Y
1 1
2
1
1
2
1 1
2
1
2
1
..
2
1 1 1
.. .. ...
Selanjutnya pengujian dilakukan sebagai U.8.2
U.8.5 Analisis Varians Dwiarah dengan Interaksi
Hipotesis :
HoA: NA1=NA2=NA3=.=NAa
HaA: ij, NAi NAj, i j, i,j=1,.,a
HoB: NB1=NB2=NB3=.=NBa
HaB: ij, NBi NBj, i j, i,j=1,.,a
HoAB: NAB11=NAB12=NAB13=.=NABab
HaAB: ijkl, NABij NABkl, ij kl, i,k=1,.,a , j,l=1,,b
21. Tabel analisis varians untuk klasifikasi dwiarah dengan interaksi
Sumber
Variansi
Derajat
Kebebasan
Jumlah
Kuadrat
Rataan
Kuadrat
F Hit Ho Tolak
Bila F Hit
A A-1 JKA
JKA
1
2
k
S A
> f ;a-1,ab(n-1)
B B-1 JKB
JKB
1
2
k
SB
2
S A
2
S B
2
S
> f ;a-1,b-1,ab(n-1)
AB (a-1)(b-1) JKAB
JKAB
abAB
S AB 2
2
S AB
2
S
> f ;a-1,(a-1)(b-1),ab(n-1)
Galat (a-1)(b-1) JKG
Total Ab-1 JKT
T.8.7.
JKT =
JKG
T
abn
a
ワワ X X 2 緒ワワ X
i
b
j
n
k
ijk
a
i
b
j
n
k
ijk
....
( ...)
2
1 1 1
2
1 1 1
JKA =
T
abn
a
bn Xi X T bn
i
i
a
i
...
( ... ...) .../( )
2
1
2
1
2
JKB =
T
abn
a
an X j X T an
i
j
b
j
...
( ... ...) ... /( )
2
1
2
1
2
a
JKAB= 2
ワ ij i
n (X X ... X j X....)
1 1
i
b
j
=
T
abn
T
ワ
an
T
bn
n
T
b
j
j
a
i
i
a
i
b
j
ij
... 2
1
2
1
2
1 1
2
JKB = JKT-JKA-JKB-JKAB
2
S
dbG
S 2
22. 8.4.UJI KESAMAAN BEBERAPA VARIANS
Misalkan K sampel acak dari poplasi normal saling bebas dengan ukuran n1,n2,,nk,
k
i
i n
1
2
1 ,...., , k SSS
=N dan varians berturut-turut 2 2
2
n
S
N K
S
k
i
gab
1
2
1 1
2
( 1)
Katakanlah :
k
2 ( ) log ( 1) log dan
a N K Sgab n
S
i
1
2
1 1
1
K n N K
h
k
i i
1
1
1
3( 1)
1
1
h = Faktor koreksi
q merupakan peubah acak ( namakan B )
Uji yang sering dilakukan uji bartlet b=2,3026 h
yang mempunyai sebaran hampiran khi kuadrat dengan derjat bebas K-1
U.8.6 Uji kesamaan Varians, dengan uji bartlet
Hipotesis:
H0 : 2 2
2
2
`1 緒 .......緒k
Ha : tidak semua varians sama
Dengan taraf signifikansi , daerah kritik B> 2
1
b=2,3026 ( g/h )
23. U.8.7 Uji bartlet menggunakan sebaran bartlet
Hipotesis :
H0 : 2 2
2
2
`1 緒 .......緒k
Ha : tidak semua varians sama
2
( )
1
2 1
gab
N K
k
l
ni
i
S
S
b
b= Merupakan nilai peubah acak B sebaran Bartlet, sehingga untuk taraf
signifikansi
a) n1=n2=.=nk=n, Daerah kritik adalah B< bk ( ;n), dimana p[b<bk ( ;n)]=
b) Ukuran sampel tidak sama , daerah kritik B< bk( ;n1,n2,.,nk), dimana
bk( ;n1,n2,.,nk) =
k
1
ni b ni
N
k
k
(; )
24. Uji varians menurut Cochran
Uji varians yang lebih sederhana dari uji bartlet adalah uji cochran uji ini menunjukkan
porsi suatu varians dari jumlah seluruh varians sampel, sehingga tampak apakah suatu
varians jauh lebih besar dari pada lainnya . Pemakaian terbatas hanya untuk ukuran sampel
yang sama n1=n2==nk=n.
U.8.8 Uji Cohran
Hipotesis
H0 : 2 2
2
`1 緒 2
.......緒k
Ha : tidak semua varians sama
G=
S terbesar
k
i
i
i
S
1
2
2
Dengan taraf signifikasi 1 Daerah kritik G>g ;k,n
25. EVALUASI
1.Diketahui ada 4 kelas siswa, tiap kelas banyak muridnya sama, sedang belajar ahasa
inggris. Masing-masing kelas diajar oleh seorang guru dan tiap guru menggunakan metoda
mengajar yang berbeda, sebut A,B,C, dan D. Nilai hasil ujian akhir proses belajar untuk tiap
metoda, rata-ratanya sbb :
Metoda A B C D
Rata-rata 67,3 76,5 56,9 63,7
Maka hitunglah varians dari nilai rata-rata tersebut
Jawab :
Anggap rata-rata ini sebagai data biasa lalu hitung variansnya.
Diperoleh varians antar kelompok A,B,C, dan D. Besarnya dihitung sebagai berikut.
Karena tiap kelas banyak muridnya sama maka rata-rata untuk keempat rata-rata itu:
村(67,3+76,5+56,9+63,7)=66,1
Jumlah kuadrat-kuadrat dikoreksi yaitu setiap data dikurangi rata-ratanya lalu dikuadratkan
dan kemudian dijumlahkan adalah
( 67,3-66,1 )2 + ( 76,5-66,1 )2 + ( 56,9-66,1 )2 + ( 63,7-66,1 )2 = 200
Bagi oleh derajat kebebasannya ialah banyak kelompok dikurangi satu jadi 4-1=3 diperoleh
varians antar kelompok A,B,C, dan D ialah sebesar 66,67.
26. 2.Varians tinggi 24 mahasiswa dalam pertandingan bola yang dipilih acak dari 50 orang.Tentukan
dalam koefisien kepkercayaan 95% selang kepercayaan untuk varians tinggi mahasiswa untuk
pertandingan bola.
Penyelesaian :
Dik. : Ukuran sampel n = 24.
S2 = 50.
= 1
= 1 95%
= 0,05.
Dit. : 2
2
x = 遜; n 1 dan x2 = 遜 (1 + j); n -1
= 遜 . 0,05; 24 1 = 遜 (1 + 0,05); 24 1
= 0,25; 23 = 0,975; 23
x2 0,025; 23 = 11,7 x2 0,975; 23 = 38,1
sehingga
2 n S
1 2
1
n S
38.1
7 .
2
n
24 1 50 2
24 1 50
38.1
11.7
98,29 30,18 2 種
27. 3.Suatu ujian teori probabilitas yang dilakukan diberikan kepada 40 orang siswa dan 60 mahasiswa.
Mahasiswi dapat rataan skors 5 dari 70 mahasiswa. Tentukan 95% selang kepercayaan selisih rataan
skor mahasiswi dengan mahasiswa apabila melalui pengalaman bahwa simpangan bakuk skor untuk
mahasiswi adalah 8 dan mahasiswa 10.
Penyelesaian :
Dik. : n1 = 60.
n2 = 40.
1 x = 70.
2 x = 55.
= 95%.
Jadi taksiran untuk 1 - 2 adalah 2 1 x x = 70 55 = 25.
a. 1 = 10, 2 = 8.
Sehingga menaksir selisih rataan :
Z遜 = 0,475 = 1,96
2
2
2
1
S
S
2
2
2
2
1
x x Z
1
1 2 1 2
2
1
1 2
2
1
2
1
S
n
S
n
x x Z
n
n
64
40
100
25 1,96 1 2
60
25 1,96
64
40
100
60
25 1,96 3,26 25 1,96 3,26 1 2 種
21,62 28,538 1 2
28. 4.Dari soal no.2 carilah simpangan baku populasi tidak diketahui tetapi mahasiswi dan mahasiswa
berasal dari satu populasi dan simpangan baku mahasiswa adalah 8 dan maka siswa adalah 10.
Penyelesaian :
Dik. : S1 = 10
S2 = 8
V = n1 + n2 2
= 60 + 40 2
= 98.
t遜 (1 + ); V = t0,975; 98 = 1,98
S2 =
n 1 S n
1
S
2
n n
1 2
2
2 2
2
1 2
=
60 1 10 2 40
1 82
60 40
2
=
5900 2496
98
= 85,67
x x t V
1 2
1 2 1 2 5
1 2
1 2 3
1 1
(1 );
1 1
(1 );
2
1
2
1
n n
x x t V
n n
1
40
1
25 1,98.85,67 1 2
60
25 1,98.85,67
1
40
1
60
9,34 59,34 1 2
![U.8.7 Uji bartlet menggunakan sebaran bartlet
Hipotesis :
H0 : 2 2
2
2
`1 緒 .......緒k
Ha : tidak semua varians sama
2
( )
1
2 1
gab
N K
k
l
ni
i
S
S
b
b= Merupakan nilai peubah acak B sebaran Bartlet, sehingga untuk taraf
signifikansi
a) n1=n2=.=nk=n, Daerah kritik adalah B< bk ( ;n), dimana p[b<bk ( ;n)]=
b) Ukuran sampel tidak sama , daerah kritik B< bk( ;n1,n2,.,nk), dimana
bk( ;n1,n2,.,nk) =
k
1
ni b ni
N
k
k
(; )](https://image.slidesharecdn.com/bab8ku-141021231333-conversion-gate02/85/analisis-varians-23-320.jpg)
