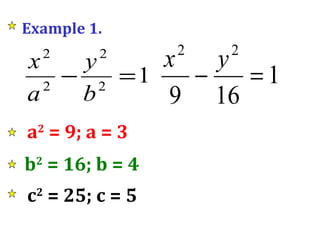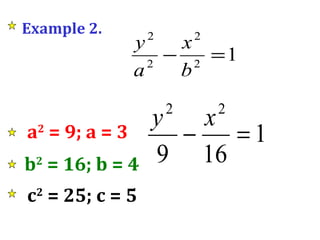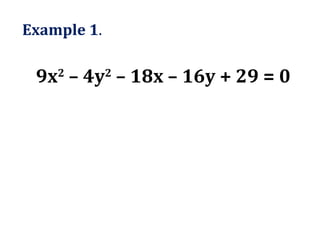Analytic geometry hyperbola
- 1. Hyperbola
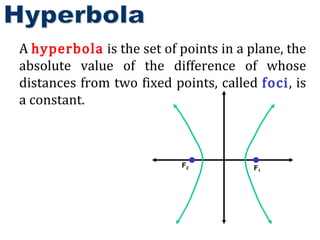
- 2. A hyperbola is the set of points in a plane, the absolute value of the difference of whose distances from two fixed points, called foci , is a constant. Hyperbola F 2 F 1
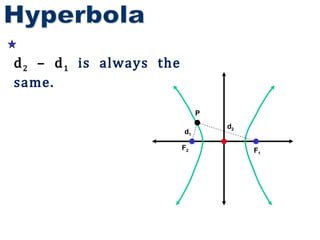
- 3. Hyperbola F 2 F 1 d 1 d 2 P d 2 ŌĆō d 1 is always the same.
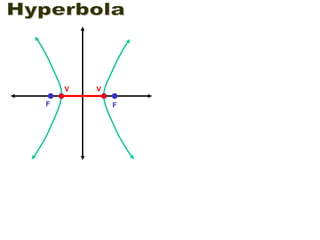
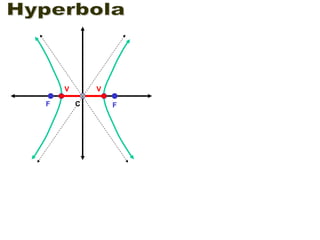
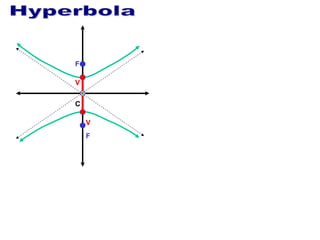
- 4. Hyperbola F F V V
- 5. Hyperbola F F V V C
- 6. Hyperbola F F V V C
- 7. Equation of a Hyperbola The center is at the point (0, 0) c 2 = a 2 + b 2 c is the distance from the center to a focus point. The foci are at (c, 0) and (-c, 0)
- 8. Equation of a Hyperbola The conjugate points are at (0, b) and (0, -b) The vertices are at (a, 0) and (-a, 0) Length of the latus rectum is 2b 2 a
- 9. Equation of a Hyperbola Ends of the latus rectum :
- 10. Equation of a Hyperbola Horizontal Hyperbola Equation of the directrix
- 11. Equation of a Hyperbola The center is at the point (0, 0) c 2 = a 2 + b 2 c is the distance from the center to a focus point. The foci are at (0, c) and (0, -c)
- 12. Equation of a Hyperbola The conjugate points are at (b, 0) and (-b, 0) The vertices are at (0, a) and (0, -a) Length of the latus rectum is 2b 2 a
- 13. Equation of a Hyperbola Ends of the latus rectum :
- 14. Equation of a Hyperbola Vertical Hyperbola Equation of the directrix
- 15. Example 1. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5
- 16. Example 1. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5 V 1 (3, 0), V 2 (-3, 0) F 1 (5, 0), F 2 (-5, 0) Center at (0, 0) Center at (0, 0) V 1 (a, 0), V 2 (-a, 0) F 1 (c, 0), F 2 (-c, 0)
- 17. Example 1. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5 LR = 2b 2 = 2(4) 2 = 32 a Conjugate points (0, 4), (0, -4) 3 3 Conjugate Points (0, b), (0, -b) LR = 2b 2 a
- 18. Example 1. LR = 2b 2 = 32 a 3 c 2 = 25; c = 5 Endpoints of LR
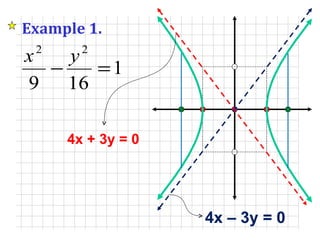
- 19. Example 1. Asymptotes c 2 = 25; c = 5 b 2 = 16; b = 4 a 2 = 9; a = 3 Asymptotes
- 20. Example 1. V 1 (3, 0), V 2 (-3, 0) F 1 (5, 0), F 2 (-5, 0) Center at (0, 0) Conjugate points (0, 4), (0, -4) Endpoints of LR Asymptotes Symmetric at x-axis
- 21. Example 1. 4x + 3y = 0 4x ŌĆō 3y = 0
- 22. Example 2. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5
- 23. Example 2. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5 V 1 (0, 3), V 2 (0, -3) F 1 (0, 5), F 2 (0, -5) Center at (0, 0) Center at (0, 0) V 1 (0, a), V 2 (0, -a) F 1 (0, c), F 2 (0, -c)
- 24. Example 2. a 2 = 9; a = 3 b 2 = 16; b = 4 c 2 = 25; c = 5 LR = 2b 2 = 2(4) 2 = 32 a Conjugate points (4, 0), (-4, 0) 3 3 Conjugate Points (b, 0), (-b, 0) LR = 2b 2 a
- 25. Example 2. LR = 2b 2 = 32 a 3 c 2 = 25; c = 5 Endpoints of LR
- 26. Example 2. Asymptotes c 2 = 25; c = 5 b 2 = 16; b = 4 a 2 = 9; a = 3 Asymptotes
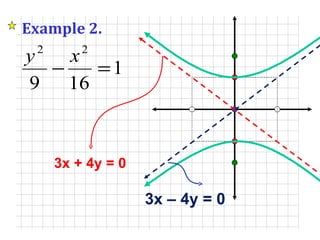
- 27. Example 2. V 1 (0, 3), V 2 (0, -3) F 1 (0, 5), F 2 (0, -5) Center at (0, 0) Conjugate points (4, 0), (-4, 0) Endpoints of LR Asymptotes Symmetric at y-axis
- 28. Example 2. 3x + 4y = 0 3x ŌĆō 4y = 0
- 29. ╠²
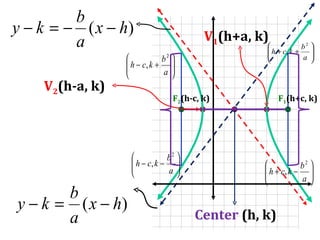
- 30. Standard Equation of a Hyperbola C (h, k)
- 31. Center (h, k) F 1 (h+c, k) F 2 (h-c, k) V 1 (h+a, k) V 2 (h-a, k)
- 32. Example 1 .
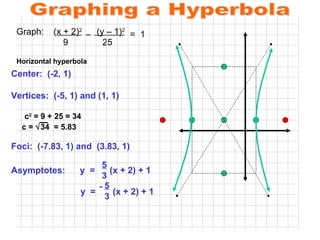
- 33. Graphing a Hyperbola Graph: ( x + 2) 2 (y ŌĆō 1) 2 9 25 c 2 = 9 + 25 = 34 c = ’ā¢ 34 = 5.83 Foci: (-7.83, 1) and (3.83, 1) ŌĆō = 1 Center: (-2, 1) Horizontal hyperbola Vertices: (-5, 1) and (1, 1) Asymptotes: y = (x + 2) + 1 5 3 y = (x + 2) + 1 5 3 -
- 34. Example 2 .
- 35. Properties of this Hyperbola Center ((1,2)
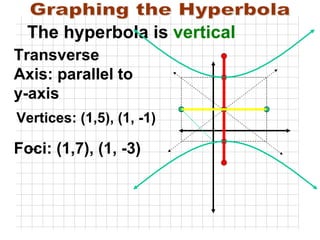
- 36. Graphing the Hyperbola Foci: (1,7), (1, -3) Vertices: (1,5), (1, -1) The hyperbola is vertical Transverse Axis: parallel to y-axis
- 37. Properties of this Hyperbola Asymptotes:
- 38. Latera Recta
- 39. ╠²
- 40. General Equation of a Hyperbola Ax 2 + By 2 + Cx + Dy + E = 0 Group the x terms together and y terms together. Complete the square. Express in binomial form. Divide by the constant term, where the first term has a positive sign.
- 41. Example 1 . 9x 2 ŌĆō 4y 2 ŌĆō 18x ŌĆō 16y + 29 = 0
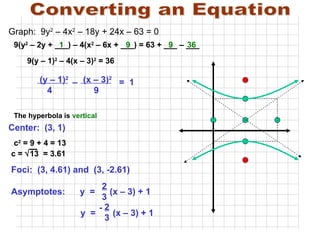
- 42. Converting an Equation (y ŌĆō 1) 2 (x ŌĆō 3) 2 4 9 c 2 = 9 + 4 = 13 c = ’ā¢ 13 = 3.61 Foci: (3, 4.61) and (3, -2.61) ŌĆō = 1 Center: (3, 1) The hyperbola is vertical Graph: 9y 2 ŌĆō 4x 2 ŌĆō 18y + 24x ŌĆō 63 = 0 9(y 2 ŌĆō 2y + ___) ŌĆō 4(x 2 ŌĆō 6x + ___) = 63 + ___ ŌĆō ___ 9 1 9 36 9(y ŌĆō 1) 2 ŌĆō 4(x ŌĆō 3) 2 = 36 Asymptotes: y = (x ŌĆō 3) + 1 2 3 y = (x ŌĆō 3) + 1 2 3 -
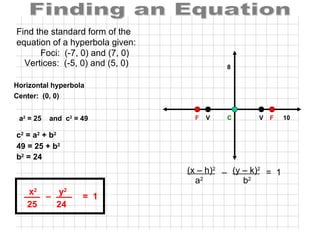
- 43. Finding an Equation Find the standard form of the equation of a hyperbola given: 49 = 25 + b 2 b 2 = 24 Horizontal hyperbola Foci: (-7, 0) and (7, 0) Vertices: (-5, 0) and (5, 0) 10 8 F F V V Center: (0, 0) c 2 = a 2 + b 2 (x ŌĆō h) 2 (y ŌĆō k) 2 a 2 b 2 ŌĆō = 1 x 2 y 2 25 24 ŌĆō = 1 a 2 = 25 and c 2 = 49 C
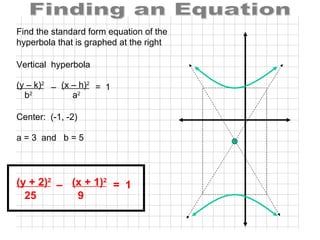
- 44. Center: (-1, -2) Vertical hyperbola Finding an Equation Find the standard form equation of the hyperbola that is graphed at the right (y ŌĆō k) 2 (x ŌĆō h) 2 b 2 a 2 ŌĆō = 1 a = 3 and b = 5 (y + 2) 2 (x + 1) 2 25 9 ŌĆō = 1
- 45. Applications M 2 M 1 An explosion is recorded by two microphones that are two miles apart. M1 received the sound 4 seconds before M2. assuming that sound travels at 1100 ft/sec, determine the possible locations of the explosion relative to the locations of the microphones. (5280, 0) (-5280, 0) E(x,y) Let us begin by establishing a coordinate system with the origin midway between the microphones Since the sound reached M 2 4 seconds after it reached M 1 , the difference in the distances from the explosion to the two microphones must be d 2 d 1 1100(4) = 4400 ft wherever E is This fits the definition of an hyperbola with foci at M 1 and M 2 Since d 2 ŌĆō d 1 = transverse axis, a = 2200 x 2 y 2 4,840,000 23,038,400 ŌĆō = 1 x 2 y 2 a 2 b 2 ŌĆō = 1 c 2 = a 2 + b 2 5280 2 = 2200 2 + b 2 b 2 = 23,038,400 The explosion must be on the hyperbola