Andrew Goldberg. An Efficient Point-to¨CPoint Shortest Path Algorithm
- 1. Point-to-Point Shortest Path Algorithms with Preprocessing Andrew V. Goldberg Microsoft Research ¨C Silicon Valley www.research.microsoft.com/¡«goldberg/ Joint with Haim Kaplan and Renato Werneck
- 2. Einstein Quote Everything should be made as simple as possible, but not simpler SP with preprocessing 1
- 3. Shortest Path Problem Variants ? Nonnegative and arbitrary arc lengths. ? Point to point, single source, all pairs. ? Directed and undirected. Here we study ? Point to point, nonnegative length, directed problem. ? Allow preprocessing with limited (linear) space. Many applications, both directly and as a subroutine. SP with preprocessing 2
- 4. Shortest Path Problem Input: Directed graph G = (V, A), nonnegative length function : A ¡ú R+ , origin s ¡Ê V , destination t ¡Ê V . Preprocessing: Limited space to store results. Query: Find a shortest path from s to t. Interested in exact algorithms that search a (small) subgraph. Related work: reach-based routing [Gutman 04], hierarchi- cal decomposition [Schultz, Wagner & Weihe 02], [Sanders & Schultes 05, 06], geometric pruning [Wagner & Willhalm 03], arc ?ags [Lauther 04], [K¡§hler, M¡§hring & Schilling 05], [M¡§hring o o o et al. 06]. SP with preprocessing 3
- 5. Motivating Application Driving directions ? Run on servers and small devices. ? Typical production codes ? Use base graph or other heuristics based on road cate- gories; needs hand-tuning. ? Runs (bidirectional) Dijkstra or A? with Euclidean bounds on ¡°patched¡± graph. ? Non-exact and no performance guarantee. ? We are interested in exact and very e?cient algorithms. ? New results ?nding their way into products. SP with preprocessing 4
- 6. Outline ? Scanning method and Dijkstra¡¯s algorithm. ? Bidirectional Dijkstra¡¯s algorithm. ? A? search. ? ALT Algorithm ? De?nition of reach ? Reach-based algorithm ? Reach for A? SP with preprocessing 5
- 7. Scanning Method ? For each vertex v maintain its distance label ds(v) and status S(v) ¡Ê {unreached, labeled, scanned}. ? Unreached vertices have ds(v) = ¡Þ. ? If ds(v) decreases, v becomes labeled. ? To scan a labeled vertex v, for each arc (v, w), if ds(w) > ds(v) + (v, w) set ds (w) = ds(v) + (v, w). ? Initially for all vertices are unreached. ? Start by decreasing ds(s) to 0. ? While there are labeled vertices, pick one and scan it. ? Di?erent selection rules lead to di?erent algorithms. SP with preprocessing 6
- 8. Dijkstra¡¯s Algorithm [Dijkstra 1959], [Dantzig 1963]. ? At each step scan a labeled vertex with the minimum label. ? Stop when t is selected for scanning. Work almost linear in the visited subgraph size. Reverse Algorithm: Run algorithm from t in the graph with all arcs reversed, stop when t is selected for scanning. Bidirectional Algorithm ? Run forward Dijkstra from s and backward from t. ? Maintain ?, the length of the shortest path seen: when scan- ning an arc (v, w) such that w has been scanned in the other direction, check if the corresponding s-t path improves ?. ? Stop when about to scan a vertex x scanned in the other direction. ? Output ? and the corresponding path. SP with preprocessing 7
- 9. Bidirectional Algorithm: Pitfalls The algorithm is not as simple as it looks. 2 a 5 b 2 s t 5 x 5 The searches meat at x, but x is not on the shortest path. SP with preprocessing 8
- 10. Example Graph 1.6M vertices, 3.8M arcs, travel time metric. SP with preprocessing 9
- 11. Dijkstra¡¯s Algorithm Searched area SP with preprocessing 10
- 12. Bidirectional Algorithm forward search/ reverse search SP with preprocessing 11
- 13. A? Search [Doran 67], [Hart, Nilsson & Raphael 68] Motivated by large search spaces (e.g., game graphs). Similar to Dijkstra¡¯s algorithm but: ? Domain-speci?c estimates ¦Ðt(v) on dist(v, t) (potentials). ? At each step pick a labeled vertex with the minimum k(v) = ds(v) + ¦Ðt(v). Best estimate of path length. ? In general, optimality is not guaranteed. 1 11 00 111111 000000 2 1 0 1111111 3 11 00 111111 0 4 1 0 00000000000000000 111111 0 1111111 0000000 11 00 111111 000000 1 0 11 00 1 0 1111111 0000000 11 00 111111 000000 1 0 11 00 1 0 1111111 0000000 111111 000000 0 4 111111 000000 3 2 1111111 0000000 1 5 1111111 0000000 11111111111 00000000000 111111 000000 1 0 11111111111 00000000000 1111111 0000000 1 0 1111111 0000000 1 0 11111111111 00000000000 1 0 1111111 0000000 11111111111 00000000000 1111111 0000000 0 11111111111 00000000000 11111111111 00000000000 1111111 0000000 1111111 0000000 1 0 1 0 11 00 111111 1 0 00000000000 111111 0 11 00 1 0 6 2 1 SP with preprocessing 12
- 14. Feasibility and Optimality Potential transformation: Replace (v, w) by ¦Ðt (v, w) = (v, w) ? ¦Ðt(v) + ¦Ðt(w) (reduced costs). Fact: Problems de?ned by and ¦Ðt are equivalent. De?nition: ¦Ðt is feasible if ?(v, w) ¡Ê A, the reduced costs are nonnegative. (Estimates are ¡°locally consistent¡±.) Optimality: If ¦Ðt is feasible, the A? search is equivalent to Dijk- stra¡¯s algorithm on transformed network, which has nonnegative arc lengths. A? search ?nds an optimal path. Di?erent order of vertex scans, di?erent subgraph searched. Fact: If ¦Ðt is feasible and ¦Ðt(t) = 0, then ¦Ðt gives lower bounds on distances to t. SP with preprocessing 13
- 15. Computing Lower Bounds Euclidean bounds: [folklore], [Pohl 71], [Sedgewick & Vitter 86]. For graph embedded in a metric space, use Euclidean distance. Limited applicability, not very good for driving directions. We use triangle inequality a000 1111111111111 0000000000000 111 b 11111111111111 00000000000000 111 000 11 11111111111111 00 00000000000000 1111111111111 0000000000000 111 000 1 0 111 000 11 11111111111111 00 00000000000000 1111111111111 0000000000000 111 000 1 0 111 000 1111111111111 0000000000000 111 000 11111111111111 00000000000000 1111111111111 0000000000000 111 000 111 000 11111111111111 00000000000000 111 000 1 0 11 00 1111111111111 0000000000000 111 000 11111111111111 00000000000000 11111111111111 00000000000000 1 0 1 0 11 00 11 00 v w dist(v, w) ¡Ý dist(v, b)?dist(w, b); dist(v, w) ¡Ý dist(a, w)?dist(a, v). SP with preprocessing 14
- 16. Lower Bounds (cont.) Maximum (minimum, average) of feasible potentials is feasible. ? Select landmarks (a small number). ? For all vertices, precompute distances to and from each land- mark. ? For each s, t, use max of the corresponding lower bounds for ¦Ðt(v). Why this works well (when it does) a s x y t ¦Ðt (x, y) = 0 SP with preprocessing 15
- 17. Bidirectional Lowerbounding Forward reduced costs: ¦Ðt (v, w) = (v, w) ? ¦Ðt(v) + ¦Ðt(w). Reverse reduced costs: ¦Ðs (v, w) = (v, w) + ¦Ðs(v) ? ¦Ðs(w). What¡¯s the problem? SP with preprocessing 16
- 18. Bidirectional Lowerbounding Forward reduced costs: ¦Ðt (v, w) = (v, w) ? ¦Ðt(v) + ¦Ðt(w). Reverse reduced costs: ¦Ðs (v, w) = (v, w) + ¦Ðs(v) ? ¦Ðs(w). Fact: ¦Ðt and ¦Ðs give the same reduced costs i? ¦Ðs + ¦Ðt = const. [Ikeda et at. 94]: use ps(v) = ¦Ðs(v)?¦Ðt(v) and pt (v) = ?ps(v). 2 Other solutions possible. Easy to loose correctness. ALT algorithms use A? search and landmark-based lower bounds. SP with preprocessing 17
- 19. Landmark Selection Preprocessing ? Random selection is fast. ? Many heuristics ?nd better landmarks. ? Local search can ?nd a good subset of candidate landmarks. ? We use a heuristic with local search. Preprocessing/query trade-o?. Query ? For a speci?c s, t pair, only some landmarks are useful. ? Use only active landmarks that give best bounds on dist(s, t). ? If needed, dynamically add active landmarks (good for the search frontier). Allows using many landmarks with small time overhead. SP with preprocessing 18
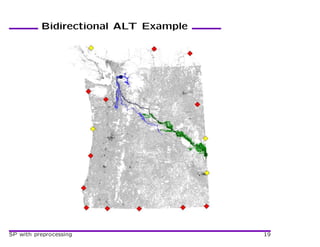
- 20. Bidirectional ALT Example SP with preprocessing 19
- 21. Experimental Results Northwest (1.6M vertices), random queries, 16 landmarks. preprocessing query method minutes MB avgscan maxscan ms Bidirectional Dijkstra ¡ª 28 518 723 1 197 607 340.74 ALT 4 132 16 276 150 389 12.05 SP with preprocessing 20
- 22. Related Systems Work Network delay estimation: Use delays to beacons to estimate arbitrary node delays. E.g., IDMaps [Francis et al. 01]. Theoretical analysis [Kleinberg, Slivkins & Wexler 04]: for ran- dom beacons and bounded doubling dimension graphs, get good bounds for most node pairs. Good bounds are not enough to prove bounds on ALT. SP with preprocessing 21
- 23. Reach Intuition Identify local intersections and prune them when searching far from s and t. SP with preprocessing 22
- 24. Reaches [Gutman 04] ? Consider a vertex v that splits a path P into P1 and P2. rP (v) = min( (P1), (P2)). ? r(v) = maxP (rP (v)) over all shortest paths P through v. Using reaches to prune Dijkstra: LB(w,t) d(s,v) v w s t If r(w) < min(d(v) + (v, w), LB(w, t)) then prune w. SP with preprocessing 23
- 25. Obtaining Lower Bounds Can use landmark lower bounds if available. Bidirectional search gives implicit bounds (Rt below). LB(w,t) d(s,v) v w s Rt t Reach-based query algorithm is Dijkstra¡¯s algorithm with prun- ing based on reaches. Given a lower-bound subroutine, a small change to Dijkstra¡¯s algorithm. SP with preprocessing 24
- 26. Computing Reaches ? A natural exact computation uses all-pairs shortest paths. ? Overnight for 0.3M vertex graph, years for 30M vertex graph. ? Have a heuristic improvement, but it is not fast enough. ? Can use reach upper bounds for query search pruning. Iterative approximation algorithm: [Gutman 04] ? Use partial shortest path trees of depth O( ) to bound reaches of vertices v with r(v) < . ? Delete vertices with bounded reaches, add penalties. ? Increase and repeat. Query time does not increase much; preprocessing faster but still not fast enough. SP with preprocessing 25
- 27. Reach Algorithm SP with preprocessing 26
- 28. Experimental Results Northwest (1.6M vertices), random queries, 16 landmarks. preprocessing query method minutes MB avgscan maxscan ms Bidirectional Dijkstra ¡ª 28 518 723 1 197 607 340.74 ALT 4 132 16 276 150 389 12.05 Reach 1 100 34 53 888 106 288 30.61 SP with preprocessing 27
- 29. Shortcuts ? Consider the graph below. ? Many vertices have large reach. 1000 1000 10 10 10 10 10 10 10 10 s 1000 1010 1020 1030 1040 1030 1020 1010 1000 t SP with preprocessing 28
- 30. Shortcuts ? Consider the graph below. ? Many vertices have large reach. ? Add a shortcut arc, break ties by the number of hops. 80 1000 1000 10 10 10 10 10 10 10 10 s t SP with preprocessing 29
- 31. Shortcuts ? Consider the graph below. ? Many vertices have large reach. ? Add a shortcut arc, break ties by the number of hops. ? Reaches decrease. s 1000 60 50 40 30 40 50 60 1000 t SP with preprocessing 30
- 32. Shortcuts ? Consider the graph below. ? Many vertices have large reach. ? Add a shortcut arc, break ties by the number of hops. ? Reaches decrease. ? Repeat. s 1000 20 10 20 30 20 10 20 1000 t SP with preprocessing 31
- 33. Shortcuts ? Consider the graph below. ? Many vertices have large reach. ? Add a shortcut arc, break ties by the number of hops. ? Reaches decrease. ? Repeat. ? A small number of shortcuts can greatly decrease many reaches. s 1000 0 10 0 30 0 10 0 1000 t SP with preprocessing 32
- 34. Shortcuts [Sanders & Schultes 05, 06]: similar idea in hierarchy-based al- gorithm; similar performance. ? During preprocessing we shortcut small-degree vertices every time is updated. ? Shortcut replaces a vertex by a clique on its neighbors. ? A constant number of arcs is added for each deleted vertex. ? Shortcuts greatly speed up preprocessing. ? Shortcuts speed up queries. SP with preprocessing 33
- 35. Reach with Shortcuts SP with preprocessing 34
- 36. Experimental Results Northwest (1.6M vertices), random queries, 16 landmarks. preprocessing query method minutes MB avgscan maxscan ms Bidirectional Dijkstra ¡ª 28 518 723 1 197 607 340.74 ALT 4 132 16 276 150 389 12.05 Reach 1 100 34 53 888 106 288 30.61 Reach+Short 17 100 2 804 5 877 2.39 SP with preprocessing 35
- 37. Reaches and ALT ? ALT computes transformed and original distances. ? ALT can be combined with reach pruning. ? Careful: Implicit lower bounds do not work, but landmark lower bounds do. ? Shortcuts do not a?ect landmark distances and bounds. SP with preprocessing 36
- 38. Reach with Shortcuts and ALT SP with preprocessing 37
- 39. Experimental Results Northwest (1.6M vertices), random queries, 16 landmarks. preprocessing query method minutes MB avgscan maxscan ms Bidirectional Dijkstra ¡ª 28 518 723 1 197 607 340.74 ALT 4 132 16 276 150 389 12.05 Reach 1 100 34 53 888 106 288 30.61 Reach+Short 17 100 2 804 5 877 2.39 Reach+Short+ALT 21 204 367 1 513 0.73 SP with preprocessing 38
- 40. Further Improvements ? Improved locality (sort by reach). ? For RE, factor of 3 ? 12 improvement for preprocessing and factor of 2 ? 4 for query times. ? Reach-aware landmarks: time/space trade-o?. ? Idea: maintain landmark distances for a small fraction of high-reach vertices only. ? Can use more landmarks and improve both time and space. Practical even for large (USA, Europe) graphs ? ¡Ö 1 ms. query time on a server. ? ¡Ö 5sec. query time on a Pocket PC with 2GB ?ash card. ? Better for local queries. SP with preprocessing 39
- 41. The USA Graph USA: 24M vertices, 58M arcs, time metric, random queries. preprocessing query method min KB avgscan maxscan ms Dijkstra ¡ª 536 11 808 864 ¡ª 5 440.49 ALT(16) 17.6 2 563 187 968 2 183 718 295.44 Reach impractical Reach+Short 27.9 893 2 405 4 813 1.77 Reach+Short+ALT(16,1) 45.5 3 032 592 2 668 0.80 Reach+Short+ALT(64,16) 113.9 1 579 538 2 534 0.86 SP with preprocessing 40
- 42. The USA Graph USA: 24M vertices, 58M arcs, distance metric, random queries. preprocessing query method min KB avgscan maxscan ms Dijkstra ¡ª 536 11 782 104 ¡ª 4 576.02 ALT(16) 15.2 2 417 276 195 2 910 133 410.73 Reach impractical Reach+Short 46.4 918 7 311 13 886 5.78 Reach+Short+ALT(16,1) 61.5 2 923 905 5 510 1.41 Reach+Short+ALT(64,16) 120.5 1 575 670 3 499 1.22 SP with preprocessing 41
- 43. Europe Graph Europe: 18M vertices, 43M arcs, time metric, random queries. preprocessing query method min KB avgscan maxscan ms Dijkstra ¡ª 393 8 984 289 ¡ª 4 365.81 ALT(16) 12.5 1 597 82 348 993 015 120.09 Reach impractical Reach+Short 45.1 648 4 371 8 486 3.06 Reach+Short+ALT(16,1) 57.7 1 869 714 3 387 0.89 Reach+Short+ALT(64,16) 102.6 1 037 610 2 998 0.91 SP with preprocessing 42
- 44. Grid Graphs Grid with uniform random lengths (0.5M vertices), 16 landmarks. No highway structure. preprocessing query method min MB avgscan maxscan ms Bidirectional Dijkstra ¡ª 18.0 174 150 416 925 160.14 ALT 0.26 96.6 6 057 65 664 6.28 Reach+Short 7.77 27.7 6 458 10 049 4.75 Reach+Short+ALT(16,1) 8.03 106.3 558 3 189 0.89 Reach+Short+ALT(64,16) 9.14 49.2 2 823 3 711 2.67 Reach preprocessing expensive, but helps queries. (64,16) signi?cantly slower that (16,1). SP with preprocessing 43
- 45. Demo SP with preprocessing 44
- 46. Concluding Remarks ? Our heuristics work well on road networks. ? Recent improvements: [Bast et al. 07, Geisberger et al. 08]. ? How to select good shortcuts? (Road networks/grids.) ? For which classes of graphs do these techniques work? ? Need theoretical analysis for interesting graph classes. ? Interesting problems related to reach, e.g. ? Is exact reach as hard as all-pairs shortest paths? ? ? Constant-ratio upper bounds on reaches in O(m) time. ? Dynamic graphs (real-time tra?c). SP with preprocessing 45



![Shortest Path Problem
Input: Directed graph G = (V, A), nonnegative length function
: A ¡ú R+ , origin s ¡Ê V , destination t ¡Ê V .
Preprocessing: Limited space to store results.
Query: Find a shortest path from s to t.
Interested in exact algorithms that search a (small) subgraph.
Related work: reach-based routing [Gutman 04], hierarchi-
cal decomposition [Schultz, Wagner & Weihe 02], [Sanders &
Schultes 05, 06], geometric pruning [Wagner & Willhalm 03], arc
?ags [Lauther 04], [K¡§hler, M¡§hring & Schilling 05], [M¡§hring
o o o
et al. 06].
SP with preprocessing 3](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-4-320.jpg)



![Dijkstra¡¯s Algorithm
[Dijkstra 1959], [Dantzig 1963].
? At each step scan a labeled vertex with the minimum label.
? Stop when t is selected for scanning.
Work almost linear in the visited subgraph size.
Reverse Algorithm: Run algorithm from t in the graph with all
arcs reversed, stop when t is selected for scanning.
Bidirectional Algorithm
? Run forward Dijkstra from s and backward from t.
? Maintain ?, the length of the shortest path seen: when scan-
ning an arc (v, w) such that w has been scanned in the other
direction, check if the corresponding s-t path improves ?.
? Stop when about to scan a vertex x scanned in the other
direction.
? Output ? and the corresponding path.
SP with preprocessing 7](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-8-320.jpg)




![A? Search
[Doran 67], [Hart, Nilsson & Raphael 68]
Motivated by large search spaces (e.g., game graphs).
Similar to Dijkstra¡¯s algorithm but:
? Domain-speci?c estimates ¦Ðt(v) on dist(v, t) (potentials).
? At each step pick a labeled vertex with the minimum k(v) =
ds(v) + ¦Ðt(v).
Best estimate of path length.
? In general, optimality is not guaranteed.
1
11
00
111111
000000
2
1
0
1111111
3
11
00
111111
0
4
1
0
00000000000000000
111111
0 1111111
0000000
11
00
111111
000000 1
0 11
00 1
0
1111111
0000000
11
00
111111
000000 1
0 11
00 1
0
1111111
0000000
111111
000000
0 4
111111
000000 3 2 1111111
0000000
1 5
1111111
0000000
11111111111
00000000000
111111
000000
1
0
11111111111
00000000000 1111111
0000000
1
0
1111111
0000000
1
0
11111111111
00000000000 1
0
1111111
0000000
11111111111
00000000000 1111111
0000000
0
11111111111
00000000000
11111111111
00000000000 1111111
0000000
1111111
0000000
1
0
1
0 11
00
111111 1
0
00000000000
111111
0
11
00 1
0
6 2 1
SP with preprocessing 12](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-13-320.jpg)

![Computing Lower Bounds
Euclidean bounds:
[folklore], [Pohl 71], [Sedgewick & Vitter 86].
For graph embedded in a metric space, use Euclidean distance.
Limited applicability, not very good for driving directions.
We use triangle inequality
a000
1111111111111
0000000000000
111
b
11111111111111
00000000000000
111
000
11 11111111111111
00 00000000000000
1111111111111
0000000000000
111
000 1
0
111
000
11 11111111111111
00 00000000000000
1111111111111
0000000000000
111
000 1
0
111
000
1111111111111
0000000000000
111
000
11111111111111
00000000000000
1111111111111
0000000000000
111
000 111
000
11111111111111
00000000000000
111
000
1
0 11
00
1111111111111
0000000000000
111
000
11111111111111
00000000000000
11111111111111
00000000000000
1
0
1
0
11
00
11
00
v w
dist(v, w) ¡Ý dist(v, b)?dist(w, b); dist(v, w) ¡Ý dist(a, w)?dist(a, v).
SP with preprocessing 14](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-15-320.jpg)


![Bidirectional Lowerbounding
Forward reduced costs: ¦Ðt (v, w) = (v, w) ? ¦Ðt(v) + ¦Ðt(w).
Reverse reduced costs: ¦Ðs (v, w) = (v, w) + ¦Ðs(v) ? ¦Ðs(w).
Fact: ¦Ðt and ¦Ðs give the same reduced costs i? ¦Ðs + ¦Ðt = const.
[Ikeda et at. 94]: use ps(v) = ¦Ðs(v)?¦Ðt(v) and pt (v) = ?ps(v).
2
Other solutions possible. Easy to loose correctness.
ALT algorithms use A? search and landmark-based lower bounds.
SP with preprocessing 17](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-18-320.jpg)


![Related Systems Work
Network delay estimation:
Use delays to beacons to estimate arbitrary node delays.
E.g., IDMaps [Francis et al. 01].
Theoretical analysis [Kleinberg, Slivkins & Wexler 04]: for ran-
dom beacons and bounded doubling dimension graphs, get good
bounds for most node pairs.
Good bounds are not enough to prove bounds on ALT.
SP with preprocessing 21](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-22-320.jpg)

![Reaches
[Gutman 04]
? Consider a vertex v that splits a path P into P1 and P2.
rP (v) = min( (P1), (P2)).
? r(v) = maxP (rP (v)) over all shortest paths P through v.
Using reaches to prune Dijkstra:
LB(w,t)
d(s,v) v w
s t
If r(w) < min(d(v) + (v, w), LB(w, t)) then prune w.
SP with preprocessing 23](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-24-320.jpg)

![Computing Reaches
? A natural exact computation uses all-pairs shortest paths.
? Overnight for 0.3M vertex graph, years for 30M vertex graph.
? Have a heuristic improvement, but it is not fast enough.
? Can use reach upper bounds for query search pruning.
Iterative approximation algorithm: [Gutman 04]
? Use partial shortest path trees of depth O( ) to bound reaches
of vertices v with r(v) < .
? Delete vertices with bounded reaches, add penalties.
? Increase and repeat.
Query time does not increase much; preprocessing faster but still
not fast enough.
SP with preprocessing 25](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-26-320.jpg)







![Shortcuts
[Sanders & Schultes 05, 06]: similar idea in hierarchy-based al-
gorithm; similar performance.
? During preprocessing we shortcut small-degree vertices every
time is updated.
? Shortcut replaces a vertex by a clique on its neighbors.
? A constant number of arcs is added for each deleted vertex.
? Shortcuts greatly speed up preprocessing.
? Shortcuts speed up queries.
SP with preprocessing 33](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-34-320.jpg)











![Concluding Remarks
? Our heuristics work well on road networks.
? Recent improvements: [Bast et al. 07, Geisberger et al. 08].
? How to select good shortcuts? (Road networks/grids.)
? For which classes of graphs do these techniques work?
? Need theoretical analysis for interesting graph classes.
? Interesting problems related to reach, e.g.
? Is exact reach as hard as all-pairs shortest paths?
?
? Constant-ratio upper bounds on reaches in O(m) time.
? Dynamic graphs (real-time tra?c).
SP with preprocessing 45](https://image.slidesharecdn.com/20080601ppspgoldberg-100622234412-phpapp01/85/Andrew-Goldberg-An-Efficient-Point-to-Point-Shortest-Path-Algorithm-46-320.jpg)