�ݺ�ߣ

Life conference and exhibition 2010
Steven Morrison and Alex McNeil

Application of Extreme
Value Theory to Risk
Capital Estimation
7-9 November 2010
© 2010 The Actuarial Profession  www.actuaries.org.uk

Application of EVT to risk capital estimation:
Agenda

• Motivation
• Background theory
• VaR case study
• Summary
• Questions or comments?

1

Application of extreme value theory to risk capital estimation

Motivation


Motivation

• Measures of risk capital are based on the (extreme) tail of a distribution
– Value at Risk (VaR)
– Conditional Value at Risk (CVaR) / Expected Shortfall

• In particular, Solvency II SCR is defined as a 99.5% VaR over a one year
horizon

• Generally needs to be estimated using simulation
1. Generate real-world economic scenarios for all risk drivers affecting the
balance sheet over one year
2. Revalue the balance sheet under each real-world scenario
– e.g. Monte Carlo („nested stochastic), Replicating Formula, Replicating Portfolio

3. Estimate the statistics of interest
3

Motivation

• An insurer who has gone through such a simulation exercise states
– “Our Solvency Capital Requirement is £77.5m”

• How confident can we be in this number?

• Many sources of uncertainty
– Choice of economic scenario generator (ESG) models and their
calibration
– Liability model assumptions e.g. dynamic lapse rules
– Choice of scenarios sampled i.e. choice of real-world ESG random
number seed

4

Motivation

• The same insurer re-runs their internal model using a different random
number seed (but all other assumptions are unchanged)
– “Our Solvency Capital Requirement is now £82.8m”

• So, simulation-based capital estimates are subject to statistical uncertainty
– Can we estimate this statistical uncertainty?
– How can we reduce the amount of statistical uncertainty?

• In this presentation, we will address these questions using a statistical
technique known as Extreme Value Theory (EVT)

5


Background theory



VaR case study


VaR Case study

Liability book
• UK-style with profits
– Management actions, dynamic EBR, dynamic bonus rates,
regular premiums

Valuation methodology
• Nested stochastic
– 1,000 real-world outer scenarios
– 1,000 risk-neutral inner scenarios per outer scenario

8

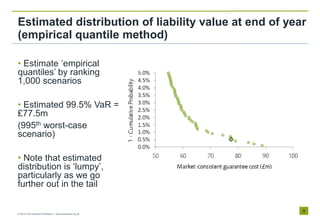
Estimated distribution of liability value at end of year
(empirical quantile method)

• Estimate „empirical
quantiles‟ by ranking
1,000 scenarios

• Estimated 99.5% VaR =
£77.5m
(995th worst-case
scenario)

• Note that estimated
distribution is „lumpy‟,
particularly as we go
further out in the tail

9

Estimated distributions using different scenario sets
(empirical quantile method)

Initial set of 1,000 real-
world scenarios
• 99.5% VaR = £77.5m

Second set of 1,000
real-world scenarios
• 99.5% VaR = £82.8m

10

What is the ‘true’ VaR?

• Two different estimates for VaR
– £77.5m
– £82.8m
– Which is „correct‟?

• Both use same (subjective) modelling assumptions
– Same economic scenario generator and calibration
– Same liability model assumptions e.g. dynamic lapse rules

• Difference is purely due to different random number streams
used to generate the economic scenarios
11

Two important questions

1. Can we reduce the sensitivity of the estimate to the choice of
random numbers?
– Run more scenarios
– May not be feasible because of model run-time

– Find a „better‟ estimator than the empirical quantile

2. Given a particular estimate of the 99.5% VaR, can we estimate
the uncertainty around this?

12

Application of Extreme Value Theory

• Recall that Extreme Value Theory tells us something about the
shape of the distribution in the tail
– Distribution of liability value beyond some threshold is
(approximately) Generalised Pareto
– Parameterised by 2 parameters

• Estimate the tail of the distribution by:
1. Picking a threshold
2. Fitting the 2 parameters of the Generalised Pareto
Distribution to values in excess of the threshold

13

Choice of threshold

20
• Choice of threshold is subjective
– But examination of „mean excess

Mean Excess (£m)
15
function‟ helps identify a suitable
choice 10

5
• We have judged that a threshold of 20 40 60 80 100
Threshold (£m)
£40m is suitable for this particular 20
case study

Mean Excess (£m)
– Approximately 26% of scenarios 15

exceed the threshold
10

5
20 40 60 80 100
Threshold (£m)

14

Estimated distributions using different scenario sets
(Extreme Value Theory method)
Initial set of 1,000 real-world
scenarios
• 99.5% VaR = £75.9m
• 95% confidence interval =
[71.1m, 84.3m]

Second set of 1,000 real-
world scenarios
• 99.5% VaR = £77.8m
• 95% confidence interval =
[72.2m, 87.7m]

15


Summary


Summary

• Simulation-based measures of risk capital, e.g. VaR, are subject
to statistical uncertainty

• Extreme Value Theory provides a robust method for estimating
VaR
– Allows statistical uncertainty to be estimated
– Statistical uncertainty lower than „naïve‟ quantile estimation
– Provides an estimate of entire tail of distribution, allowing estimate of
more extreme VaR, CVaR etc.

17

Questions or comments?

Expressions of individual views by
members of The Actuarial Profession
and its staff are encouraged.
The views expressed in this presentation
are those of the presenter.

18

�ݺ�ߣ

Application of Extreme Value Theory to Risk Capital Estimation

More Related Content

Application of Extreme Value Theory to Risk Capital Estimation