Applications of Linear Algebra in Computer Sciences
- 1. APPLICATIONS OF LINEAR ALGEBRA IN COMPUTER SCIENCES Hafiz Muhammad Amir Sharif SP12-BSCS-B7(B)-110
- 2. Objectives ?Importance of Linear Algebra ?Graph Theory ?Network Models ?Cryptography ?Computer Graphics
- 3. Why Linear Algebra is important ? ? Linear algebra is vital in multiple areas of science in general. Because linear equations are so easy to solve, practically every area of modern science. ? It converts large number of problems to matrix and thus we solve the matrix.
- 4. Graph Theory
- 5. Network Models ? Determine the currents I1, I2, and I3 for the following electrical network:
- 7. Cryptography ? Encryption and decryption require the use of some secret information, usually referred to as a key. ? Example Let the message be ¡°PREPARE TO NEGOTIATE¡± ? We assign a number for each letter of the alphabet.
- 8. Thus the message becomes: ? Since we are using a 3 by 3 matrix, we break the enumerated message above into a sequence of 3 by 1 vectors:
- 9. By multiplying encoding matrix to this matrix we will encrypt the msg
- 10. Now to decrypt the msg we have to multiply this matrix to Inverse of encoding matrix ? The inverse of this encoding matrix, the decoding matrix, is: ? Multiplying again by this matrix we will get our Msg.
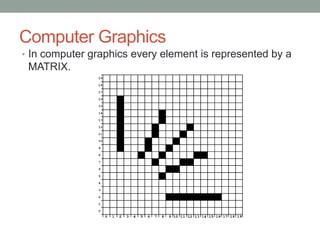
- 11. Computer Graphics ? In computer graphics every element is represented by a MATRIX.
- 12. Conclusion: ? There are so many application of Linear Algebra in Computer Science. ? From simple circuit solving to large web engine algorithms.
- 13. Thank you