![部分点解法 その1
? 毎回どの建物を増築するかを? 通りから選ぶ解
法だと O(? ?
) 通りになってしまう。
? 考えてみると、異なる建物同士の増築の順番を
考慮しなくてもよいことが分かる。
? つまり、「建物1 を増築しまくる」→ 「建物2 を増築
しまくる」→… という順番を付けてもOK。
? すると、dp[i][j]=(i 番目の建物までの増築が完了
したときに、今まで j 回増築している場合の最小
費用) とする DP を組めば O(?2
?) で計算するこ
とができる。これで 30 点が得られる。](https://image.slidesharecdn.com/arc021-140419031740-phpapp01/85/AtCoder-Regular-Contest-021-16-320.jpg)
AtCoder Regular Contest 021 解説
- 1. AtCoder Regular Contest 021 解説 AtCoder株式会社 2014/4/19 1
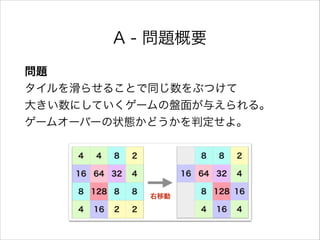
- 2. A問題 DEAD END
- 5. A - 解き方 整理すると……? 上下左右に隣り合う同じ数が ある?→?CONTINUE? ????????????? ない?→?GAMEOVER 実装? ?2 重ループを回す（添字に注意）? ?if 文を書きまくって全部調べる（列挙漏れに注意）? (きちんとループで書けるようになっておいた方がいい)
- 6. ARC #021 B 問題解説 解説:城下 慎也 (@phidnight)
- 7. 問題概要 ? ? 個の非負整数 ?1, ?2, … , ? ? が与えられる。 ? ?? = ??＾??+1(ただし ? ?+1 = ?1) である。 (以降、＾ を排他的論理和(xor) の記号として表す。) ? ?1, ?2, … , ? ? として考えられるものが存在するな ら辞書順最小を求めよ。ないならないことを指摘 せよ。 ? 2 ≦ ? ≦ 100,000
- 8. 排他的論理和の性質(例) ? ?, ?, ? を非負整数とすると ? 結合則(?＾?)＾?= ?＾(?＾?) が成立する。 ? 交換則?＾?= ?＾? が成立する。 ? ?＾0= ? (零元) ? ?＾?= 0 (それ自身と xor すると零元になる。) ? これらの性質を利用してこの問題を考える。
- 9. 考察 ? ?1を固定して考えてみる。 ? ?1 =?1＾ ?2より?2=?1＾ ?1 (∵ ?2=0＾?2=(?1＾?1)＾?2=?1＾(?1＾?2)=?1＾ ?1) ? 同様に、 ?2 =?2＾ ?3より?3=(?1＾?1)＾?2 (∵ ?3=?2＾?2=前述の?2を代入) ? 一般に ??=?1＾?1＾?2＾…＾???1 (? ≧ 2)が成立 することを示す。
- 10. 考察 ? ??=?1＾?1＾?2＾…＾???1 (? ≧ 2)が成立する。 (∵??=(?1＾?1)＾(?2＾?2)＾…＾(???1＾???1)＾?? =?1＾(?1＾?2)＾ (?2＾?3) ＾…＾(???1＾??) =?1＾?1＾?2＾…＾???1) ? 以上のことより、?1が定まれば、?2から? ?ま でのすべての値が?1から? ??1までの値を用 いて、一意に定まることがわかる。
- 11. 解の存在判定について ? 使用されなかった? ?については、先ほどの計 算で出てきた値と? ?= ? ?＾ ?1が矛盾する場 合がある。 ? ? ?＾ ?1= ?1＾ ?2＾…＾ ? ??1となるので? ?は?1 に依存せずこの値に一致するはずである。 ? 矛盾したならば解が存在しない。 ? 矛盾しないなら、 ?1を任意に指定した後、解 が一意に定まる。
- 12. 辞書順最小 ? 解が存在した場合に、辞書順最小なものを求 める必要がある。 ? 先頭の値 (?1) ができるだけ小さいほうが良 い。 ? 今回の場合では、?1=0のケースがただ 1 通 りだけ存在するので、その1 通りが辞書順最 小の値となる。(?2以降を比較する必要はな い。) ? これを計算して答えが得られる。
- 13. まとめ ? ? ?=?1＾ ?2＾…＾ ? ??1が成立しないなら解なし、 成立するなら?1= 0と置いて順に解を計算す る。 ? 排他的論理和の性質を利用した問題は様々 なものがあるので、排他的論理和の問題に は慣れておこう!
- 14. ARC #021 C 問題解説 解説:城下 慎也 (@phidnight)
- 15. 問題概要 ? 高橋君は建物を ? 回増築したい。 ? 高橋君は ? 軒の建物を所有している。 ? 増築には、増築する建物について、現在の価格 だけ費用がかかり、増築で一定値値上がりする。 ? 合計費用として考えられるものの最小値はいくら か。 ? 1 ≦ ? ≦ 100,000,000 ? 1 ≦ ? ≦ 100,000
- 16. 部分点解法 その1 ? 毎回どの建物を増築するかを? 通りから選ぶ解 法だと O(? ? ) 通りになってしまう。 ? 考えてみると、異なる建物同士の増築の順番を 考慮しなくてもよいことが分かる。 ? つまり、「建物1 を増築しまくる」→ 「建物2 を増築 しまくる」→… という順番を付けてもOK。 ? すると、dp[i][j]=(i 番目の建物までの増築が完了 したときに、今まで j 回増築している場合の最小 費用) とする DP を組めば O(?2 ?) で計算するこ とができる。これで 30 点が得られる。
- 17. 部分点解法 その2,3 ? 実は、毎回「現在の費用が最小なものを増築 し続ける」という貪欲法で正解を得ることがで きる。 ? 以降の数枚でそのことを示す。 ? この貪欲法を毎回すべて見る方針で実装す れば O(??) で解ける。計40点が得られる。 ? priority_queue を使用すればO(? log ?) とな り、通算55点が得られる。
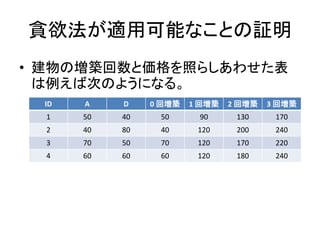
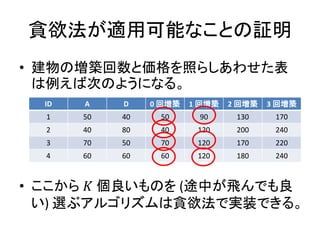
- 18. 貪欲法が適用可能なことの証明 ? 建物の増築回数と価格を照らしあわせた表 は例えば次のようになる。 ID A D 0 回増築 1 回増築 2 回増築 3 回増築 1 50 40 50 90 130 170 2 40 80 40 120 200 240 3 70 50 70 120 170 220 4 60 60 60 120 180 240
- 19. 貪欲法が適用可能なことの証明 ? 建物の増築回数と価格を照らしあわせた表 は例えば次のようになる。 ? ここから ? 個良いものを (途中が飛んでも良 い) 選ぶアルゴリズムは貪欲法で実装できる。 ID A D 0 回増築 1 回増築 2 回増築 3 回増築 1 50 40 50 90 130 170 2 40 80 40 120 200 240 3 70 50 70 120 170 220 4 60 60 60 120 180 240
- 20. 貪欲法が適用可能なことの証明 ? 先ほどの貪欲アルゴリズムは左詰め。という のも、同じ ID 内で、X 回増築の部分を採用し ないで X+1 回増築の部分を採用しているなら、 代わりに X 回増築の部分を採用すればより 費用が下がる。 ? 左詰めに採用されているのであれば、これは 今回の問題で実行可能。 ? この値より下回る解は存在しないので、これ が最適解となる。
- 21. 満点解法に向けて ? この方針では 1 ≦ ? ≦ 100,000,000 という制 約に対して充分高速でない。 ? 今までの手順をどうにかして高速化したい。 ? 更に考察してみよう!
- 22. アプローチを変えてみる ? 貪欲法で最後に選んだ増築の費用を?として みる。 ? 費用が?の増築に対して、 ? ? > ?なら、その増築は必ず行われる。 ? ? < ?なら、その増築は決して行われない。 ? ? = ?なら、合計が?回となる分だけ増築が 行われる。
- 23. 満点解法 ? 先ほどの?を考えてみると、適当に?′を定めたと き、 ?′未満、 ?′より大きい、 ?′に等しい費用の増 築がそれぞれ何個あるかを計算すれば、?と?′ の大小関係が分かる。 ? よって、 ?を二分探索することで計算することが できる。 ? ?が分かれば、 ?未満の増築(?個とする)をすべ て採用し、 ?と等しい増築を? ? ?個採用すれ ば最適解を計算できる。 ? O(? log ?) (?は?の上限) で計算できる。 ? 100点が得られる。
- 24. D問題 だいたい最小全域木
- 25. D - 問題概要 問題? 200 次元空間に 5 000 個の点がある。? 2 点を結ぶコストを (1 - コサイン類似度) とするとき? できるだけコストの小さい全域木を求めよ。? 最適なものの 1.01 倍のコストに収まれば OK。
- 26. D - 方針 普通にやると……? 問題自体は最小全域木だが、? 全点間のコストを計算するのは時間がかかりすぎる。 最小じゃなくてもいい！? 「最適なものの 1.01 倍のコストに収まれば OK。」? だった！? → 必要そうな 2 点間だけ計算するようにしたい
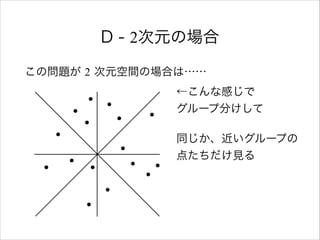
- 27. D - 2次元の場合 この問題が 2 次元空間の場合は…… ←こんな感じで? グループ分けして 同じか、近いグループの? 点たちだけ見る
- 28. D - 200 次元でも同じことを ?ランダムなベクトルを K 個用意する? ?各点とランダムベクトルの内積が正か負かで? ?K ビットのハッシュのようなものが計算できる? ?このハッシュで近いものだけを考えることにする ハッシュ同士はハミング距離(異なるビットの個数)? で距離を測れば爆速！！！！！
- 29. D - K の選び方 今回の場合は点がランダムに分布しているので ?点の i 番目の座標の値が正か負か で 200 ビットのハッシュを作ると、? 均等にグループ分けできて良いです。