![A-分割の仕方
● あるサイズの靴がいくつあるか数える
– L[i] := サイズ i の左足の靴がいくつあるか
– R[i] := サイズ i の左足の靴がいくつあるか
– 入力のたびにインクリメントする事によって求まる](https://image.slidesharecdn.com/arc024-140531083339-phpapp01/85/AtCoder-Regular-Contest-024-4-320.jpg)
![A-まとめ
● 各サイズについて左右いくつずつあるか数える
● 各サイズについていくつペアが作れるかを調べ
る
– L[i]とR[i]の最小値を取ることによって求まる
● それらの総和が答えとなる](https://image.slidesharecdn.com/arc024-140531083339-phpapp01/85/AtCoder-Regular-Contest-024-5-320.jpg)
![D-参考
● 次のような処理をしても、条件に合うバス停の
置き方ができる
● 登場するxの値を管理する二分探索木を作る
● yの値が小さい順に予め設置してあるバス停を
見ていき、その二分探索木でその点のxの値を
探索する
● 探索の過程で通過した頂点の値を[a1, a2...]とす
る
● (a1, y) (a2, y)... を追加していく](https://image.slidesharecdn.com/arc024-140531083339-phpapp01/85/AtCoder-Regular-Contest-024-43-320.jpg)
AtCoder Regular Contest 024 解説
- 2. A-問題概要 ● 左足の靴がL足、右足の靴がR足あり、それぞれ のサイズが与えられる ● 両足のサイズが同じになるようペアを作ると き、最大で何組のペアを作成できるか？ ● 1 ≦ L, R ≦ 100 ● 10 ≦ 靴のサイズ ≦ 40
- 3. A-問題の分割 ● あるサイズの靴が、違うサイズの靴のペアを作 成できるかどうかに影響しないので、同じサイ ズどうしに分けて独立の問題として解いて良い ● サイズ に対して、左足が 足、右足が 足あ るとき、最大で何組のペアを作成できるか？ – 明らかに と の最小値を取れば良い LS RSS LS RS
- 4. A-分割の仕方 ● あるサイズの靴がいくつあるか数える – L[i] := サイズ i の左足の靴がいくつあるか – R[i] := サイズ i の左足の靴がいくつあるか – 入力のたびにインクリメントする事によって求まる
- 5. A-まとめ ● 各サイズについて左右いくつずつあるか数える ● 各サイズについていくつペアが作れるかを調べ る – L[i]とR[i]の最小値を取ることによって求まる ● それらの総和が答えとなる
- 7. B-問題概要 ● 環状に並んだ赤もしくは黒の木がN個ある ● 1日ごとに隣の状況をみて色が変化する – 自分と両隣の色が同じなら異なる色に変化 ● 変化がなくなるまでの日数を求めよ ● 3 ≦ N ≦ 100,000
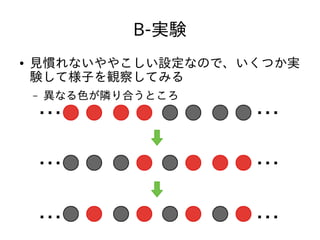
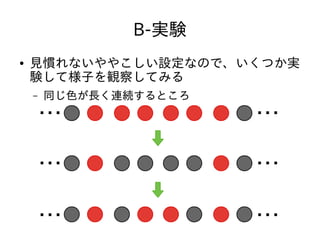
- 10. B-実験 ● 隣に異なる色がいる木はそれ以降ずっと変わら ない – 連続する同じ色の塊にわけて考えて良い ● X個連続して同じ色が並ぶと ［(X-1) / 2］日後 に止まる – ただし［x］はxを超えない最大の整数を表す ということがわかる
- 11. B-環状 ● どうやら、連続する部分を数えて適当な演算を し、最大値を取れば答えが出るらしい ● しかし、木が環状に並んでいるので少しややこ しい ● 環状ではなくしたい – 適切な場所で切り、1列に変換する ● 適切な場所とは？ – 異なる色が隣り合っているところ
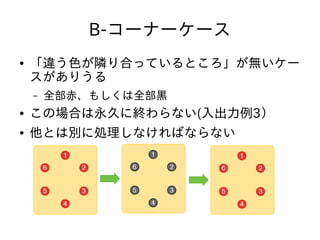
- 12. B-コーナーケース ● 「違う色が隣り合っているところ」が無いケー スがありうる – 全部赤、もしくは全部黒 ● この場合は永久に終わらない(入出力例3） ● 他とは別に処理しなければならない
- 13. B-まとめ ● 全部同じ色かどうか調べる – 全部同じだったら出力は -1 ● 異なる色が隣り合う場所で切り1列にする ● 同じ色が連続する塊に分け、それらの色が変わ らなくなるまでの日数を求める – 長さがXならば［(X-1) / 2］日後 ● それらの最大値が答えとなる
- 14. ARC #024 C 問題解説 解説:城下 慎也 (@phidnight)
- 15. 問題概要 ? 長さ ? の文字列が与えられる。 ? ある長さ ? の(連続)部分文字列を 2 箇所で 取る。 ? 両者が共通部分を持たず、かつ一方が他方 のアナグラムとなっているものがあるか。 ? 例: abcdbcae だと、 abcdbcae という 2 箇所 abc と bca は共通部分を持たず、かつ一方が 他方のアナグラムとなっている。 ? 1 ≦ ? ≦ ? ≦ 100,000
- 16. 部分点解法 その1 ? アナグラムかどうか判定する 2 箇所の候補す べてを考えてみる。 ? 開始点は左から 1 番目～ ? ? ? + 1 番目ま でが選べるので、 ?(?2 ) 通りの組み合わせ がある。 ? 各組み合わせで ?! 通りのアナグラムの割り 当てがあるので、全て試す方針で?(?2 ?!) 。 これで 15 点が得られる。
- 17. 部分点解法 その2,3 ? アナグラムであることと、各文字の出現回数 が一致していることが同値であることを利用 する。 ? 1 文字ずつ数えて出現回数を見る方針だと全 体で? ?2 ? で計算できる。30 点が得られ る。 ? 上記の計算で、文字種ごとの累積和を用いる と? ?2 になり、 45 点が得られる。
- 18. 満点解法に向けて ? 部分点解法で行っていたことは、 ? ? ? + 1 通りの始点候補のうち、始点から ? 文字所 得した際の各文字の出現回数が一致する 2 箇所が存在するか判定することであった。 ? 各文字(26通り)の出現回数は、これを大きい 整数と思うことで、次の問題に帰着することが できる。
- 19. 帰着した問題 ? 入力: 整数 ? と ? 個の整数。 ? 出力: ? 個の整数のうち 2 回以上出てくる整 数が存在するか(YES or NO)。 ? この問題は、すべてのペアを試すと? ?2 の 計算量となるが、ソートして隣り合うペアのみ を見る/二分探索木を使用することで ? ? log ? で計算できる。
- 20. 満点解法 ? 累積和などで、 ? ? ? + 1 通りの始点候補に 対する、そこから ? 文字とったときの各文字 の出現回数をO ? で計算しておく。 ? 求めた値をキーとしてソートをするか、二分探 索木を用いることで? ? log ? で判定する。 ? 全体で? ? log ? となり、100点が得られる。
- 21. 満点解法(別解) ? 出現回数から算出したハッシュ関数を使用す ることでも高速に計算できる。 ? ただし、ハッシュの衝突に注意。 ? 复数キー用意するとより安全。
- 22. ARC024解説 D:バス停
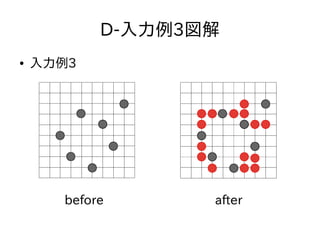
- 23. D-問題概要 ● 1,000×1,000の座標上にN個バス停が置かれる ● 1つのバスはx軸かy軸のどちらかに平行な移動 しかできない – バス停で乗り換えればいろいろなところに行ける ● どのバス停間も乗り換えのみで総移動距離がマ ンハッタン距離と等しくなるような移動ができ るようにする ● 合計が10,000個を超えないように新たなバス 停を追加せよ ● 1 ≦ N ≦ 1,000
- 26. D-考察 ● 全ての格子点にバス停を置けば明らかに条件を 満たす – 格子点は1,000×1,000個あり、全て埋めると制約 を軽く超えてしまう ● 追加前に1つもバス停がない列や行はないもの として考えて良い – 座標圧縮ができる
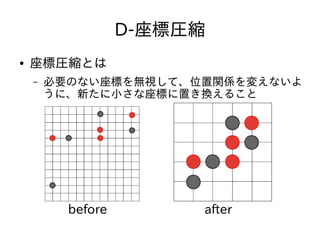
- 28. D-座標圧縮 ● 圧縮の仕方 – 圧縮前後で頂点の位置関係が変わっていなければ良 い – 位置関係というのはxやyの大小関係 – 出てくるxの種類について小さい順に1から番号を 振っていく、それを圧縮後の座標とすればよい ● 例: {3, 5, 10, 23} → {1, 2, 3, 4} – yについても同様
- 29. D-座標圧縮 ● 圧縮後の性質 – xの値とyの値が全て違ったとしても、それぞれたか だかN種類しかない – 圧缩后は狈*狈より以下のサイズになる
- 30. D-部分点1 ● 座標圧縮した後に、すべての格子点をバス停で 埋める ● 合計で最大N*N個のバス停を置くことになる ● 部分点1(N ≦ 100) 分の点数を獲得できる
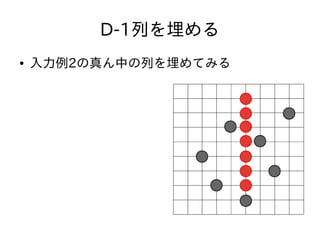
- 31. D-考察2 ● さすがに格子点を全部埋めるのは無駄が多すぎ る ● 1列だけというのはどうだろう？ ● ある1列を選んでその列すべての格子点にバス 停をおいたときどうなるか考える
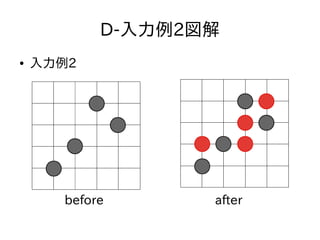
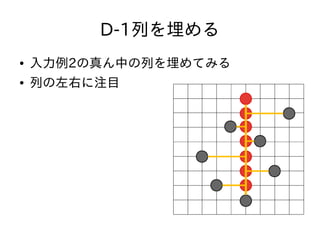
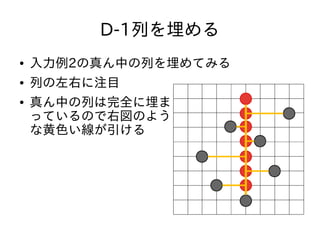
- 34. D-1列を埋める ● 入力例2の真ん中の列を埋めてみる ● 列の左右に注目 ● 真ん中の列は完全に埋ま っているので右図のよう な黄色い線が引ける
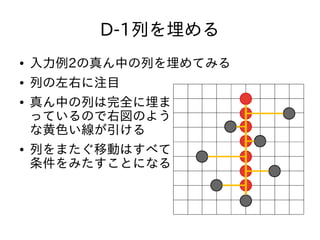
- 35. D-1列を埋める ● 入力例2の真ん中の列を埋めてみる ● 列の左右に注目 ● 真ん中の列は完全に埋ま っているので右図のよう な黄色い線が引ける ● 列をまたぐ移動はすべて 条件をみたすことになる
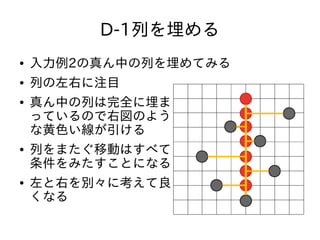
- 36. D-1列を埋める ● 入力例2の真ん中の列を埋めてみる ● 列の左右に注目 ● 真ん中の列は完全に埋ま っているので右図のよう な黄色い線が引ける ● 列をまたぐ移動はすべて 条件をみたすことになる ● 左と右を別々に考えて良 くなる
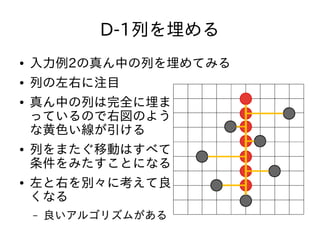
- 37. D-1列を埋める ● 入力例2の真ん中の列を埋めてみる ● 列の左右に注目 ● 真ん中の列は完全に埋ま っているので右図のよう な黄色い線が引ける ● 列をまたぐ移動はすべて 条件をみたすことになる ● 左と右を別々に考えて良 くなる – 良いアルゴリズムがある
- 38. D-1列を埋める 分割統治
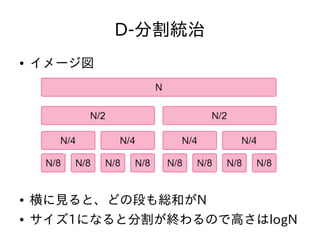
- 39. D-分割統治 ● ある問題のサイズNのバージョンを解くのに必 要な計算の回数をf(N)とする – f(1) = O(1)が成り立つとする ● サイズNの問題はO(N)の計算でサイズがN/2の 問題2つに分割することができるとする – f(N) = O(N) + 2 * f(N/2) となる ● これを解くとf(N) = O(N log N)となる
- 40. D-分割統治 ● イメージ図 ● 横に見ると、どの段も総和がN ● サイズ1になると分割が终わるので高さは濒辞驳狈
- 42. D-想定解 ● 左右で個数が2等分されるような列を選ぶ – N個のバス停を設置 ● N/2個のバス停の処理を2回する ● 同様に分割統治の要領で再帰していく ● サイズが半分になっても座標は大きいままなの で、毎回座標圧縮することを忘れないように ● 合計でNlogN個のバス停を置くことになる ● NlogN ＜ 10,000なので満点が得られる
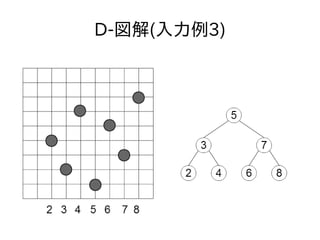
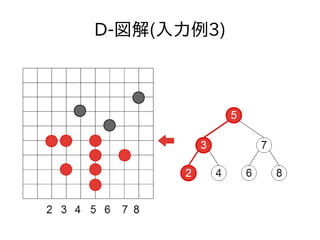
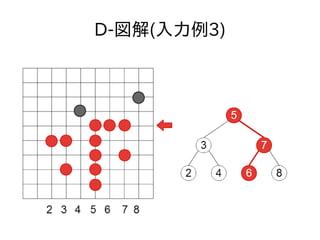
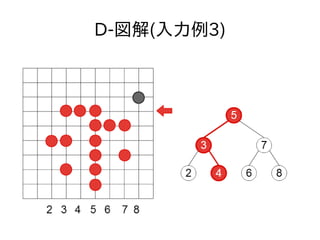
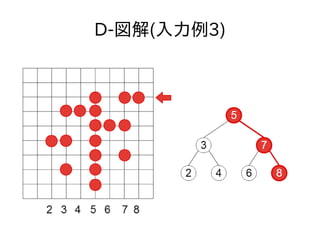
- 43. D-参考 ● 次のような処理をしても、条件に合うバス停の 置き方ができる ● 登場するxの値を管理する二分探索木を作る ● yの値が小さい順に予め設置してあるバス停を 見ていき、その二分探索木でその点のxの値を 探索する ● 探索の過程で通過した頂点の値を[a1, a2...]とす る ● (a1, y) (a2, y)... を追加していく
- 44. 顿-図解(入力例3)
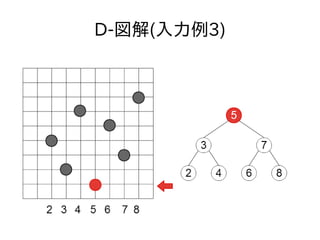
- 45. 顿-図解(入力例3)
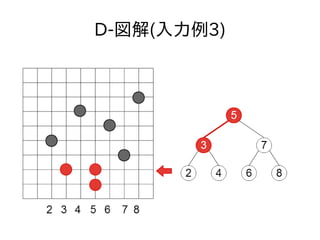
- 46. 顿-図解(入力例3)
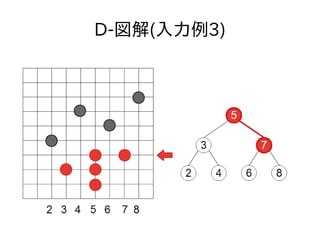
- 47. 顿-図解(入力例3)
- 48. 顿-図解(入力例3)
- 49. 顿-図解(入力例3)
- 50. 顿-図解(入力例3)
- 51. 顿-図解(入力例3)
- 52. D-参考 ● 先の例のように完全二分探索木を使えば探索時 に触れる点の個数がたかだかlogN個なので個数 制限にもひっかからない – AC – よく考えると分割統治の解と同値であることがわか る ● 実は使う二分探索木は現れるxの値だけでな く、1～1000のすべての値を持っていても大丈 夫 – 座標圧縮や再帰がなくなるので、実装が分割統治よ り楽になる
- 53. D-参考（発展） ● 完全二分探索木ではない二分探索木を使うこと も可能 ● 実は、「回転」と呼ばれる操作が許されるので 平衡二分探索木でも可能 – ただし定数倍が重く、個数制限に引っかかりWA ● なぜ可能かの証明は難しいので割愛 – Geometry of binary search treesなどのキーワード で検索すると詳細な情報が出てくる