AtCoder Regular Contest 032 解説
- 1. AtCoder Regular Contest 032 解説 AtCoder株式会社 代表取締役 高橋 直大 2015/1/3 1
- 2. 競技プログラミングを始める前に ? 競技プログラミングをやったことがない人へ – まずはこっちのスライドを見よう! – http://www.slideshare.net/chokudai/abc004 2015/1/3 2
- 3. ?AtCoder Inc. All rights reserved. 3 A問題 ホリドッグ 1. 問題概要 2. アルゴリズム 2015/1/3 3
- 4. A問題 問題概要 ? Nが与えられる ? 1+2+…+Nの素数判定せよ ? 制約 – 1 ≦ N ≦ 999 2015/1/3 4
- 5. A問題 アルゴリズム ? 解法1 – S=1+2+…+Nをforループで計算する ? N=1000のとき最大でS=1+2+…+1000 = 500500 – それに対して素数判定をforループで行う ? 2~S-1の範囲でSを割り切る数がないか確かめる ? 解法2 – S=1+2+…+N= ? ?+1 2 (総和の公式) ? 式から明らかにNが小さいとき以外は素数にならなさそう – N=1のときは1なので素数ではない – N=2のときは素数 – N>2のとき常に合成数 ? N=2のときだけ素数,それ以外のとき非素数なので, その事実にしたがって出力すればよい 2015/1/3 5
- 6. ?AtCoder Inc. All rights reserved. 6 B問題 道路工事 1. 問題概要 2. アルゴリズム 2015/1/3 6
- 7. B問題 問題概要 ? N 頂点 M 辺の無向グラフが与えられる ? グラフに最小でいくつ辺を追加すれば、全体がつな がるか調べる ? 制約 – 0 ≦ N,M ≦ 100000 2015/1/3 7
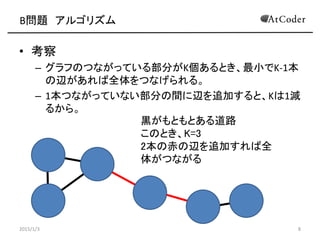
- 8. B問題 アルゴリズム ? 考察 – グラフのつながっている部分がK個あるとき、最小でK-1本 の辺があれば全体をつなげられる。 – 1本つながっていない部分の間に辺を追加すると、Kは1減 るから。 2015/1/3 8 黒がもともとある道路 このとき、K=3 2本の赤の辺を追加すれば全 体がつながる
- 9. B問題 アルゴリズム ? なので、グラフのつながっている部分(連結成分と呼 ばれる)の数を数えればよい。 ? 解法1 – Union-Findですべての辺をつないだ後、Union-Find木での root の数を数える(具体的には、頂点 v のrootが v のもの を数えると楽。連結成分ごとに root は共通で、自身が root となるものがちょうど 1 つあるから) ? 解法2 – 今まででまだ訪れていない頂点を見つけたら、 DFSを使い そこから行ける頂点をすべて訪れて、連結成分の数を1つ 加える etc… ? どちらも(ほぼ)線形時間 2015/1/3 9
- 10. ?AtCoder Inc. All rights reserved. 10 C問題 仕事計画 1. 問題概要 2. アルゴリズム 2015/1/3 10
- 11. C問題 問題概要 ? 時刻の区間がN個与えられます。区間は順に1から Nまで番号付けられています。 ? i 番目の区間は a_i から b_i まで。 ? 互いに被らない条件の下で、なるべく多くの区間を 選びたい(端点は被ってもOK) ? 複数あるときは、区間の早い順に並べた時の辞書 順最小となるものを1つ出力。 ? 制約 – 0 ≦ a_i, b_i ≦ 1000000 – 1 ≦ N ≦ 100000 2015/1/3 11
- 12. C問題 アルゴリズム ? これ蟻本でやったやつだ!(区間スケジューリング問 題, p43) – 蟻本を読もう! – 具体的には、終了時間が早い順にソートし、貪欲に区間 を選んで行けば、区間数最大の解が1つ得られる ? しかし、辞書順最小での構成を1つ出力しなければ ならない ? なるべく多く取れる取り方のうち、辞書順最小のもの を求めるときは、最初に取れるものを最小化し続け る必要がある 2015/1/3 12
- 13. C問題 アルゴリズム ? 時刻 i それぞれに対し、(i 以降で最大でいくつ取れ るか?,最大の取り方のうち、次に取れる最小の仕事 の番号はいくつか?) のペアが更新すればできそう – i から始めるとき、次に取る区間は辞書順最小の条件か ら、(最大の取り方のうち、次に取れる最小の仕事の番号) となるから ? このペアを dp[i] とおく 2015/1/3 13
- 14. C問題 アルゴリズム ? dp[i] を求めるとき、 – 時刻 i から始まる区間を使うとき、時刻 i から始まり、b で終わ る番号idの区間を使う場合、 (b以降で取れる区間の最大数 +1,id) が候補 – 時刻 i から始まる区間を使わないとき、(時刻 i+1 以降で取れる 区間の最大数, そのうちの最小の仕事の番号) が候補 – 以上のペアから、取れる区間の最大数で比較し、多いものを選 ぶ。それが同じなら、次に取る仕事の番号が小さいものを選ぶ。 ? 番号が同じ区間はないので、このペアが同じになることは無い ? 以上のことから、dp[i] の更新に必要なのは i+1 以降の dpの情報 ? よって、dp[i] を後ろから更新していけばよい 2015/1/3 14
- 15. C問題 アルゴリズム ? dp[0] が求まったら、0 以降で取れる区間の最大数 が1つ目の答え。 ? 復元するときは、今の時刻以降で最大の取り方のう ち最小の番号の区間をとり続けていく – dp のペアの2番目の情報にこれがそのまま入っている – 最初に “今の時刻”=0 とし、次に取る区間を答えに追加 し、”今の時刻”を最後に取った区間の終端に更新 – これを、取れる区間が無くなるまで繰り返す ? 合計でもO(N)! 2015/1/3 15
- 16. ?AtCoder Inc. All rights reserved. 16 D問題 アットコーダーモンスターズ 1. 問題概要 2. 考察 3. アルゴリズム 2015/1/3 16
- 17. D問題 問題概要 ? N匹のモンスターがいる ? 各モンスターには攻撃力と防御力というパラメータがある ? ちょうどK匹のモンスターを買いたい ? あるモンスターの対について,攻撃力の差と防御力の差の 最大値を不安定度と定義 ? K匹からなるチームに含まれるペアの不安定度の最大値 (=チームの不安定度)を最小化し,それを達成する組み合わ せ数 mod 100000007 を出力しろ. ? 制約 – 1 ≦ K ≦ N ≦ 100,000 – 0 ≦ 各モンスターの防御力,攻撃力 ≦ 3000 2015/1/3 17
- 18. D問題 考察 ? まず,チームの不安定度の最小値を求めたい. ? モンスターの(攻撃力,防御力)を二次元平面に点とし てプロットしてみる ? あるチームの不安定度をxと決めたとき, – 一辺xの正方形領域に含まれる点の数がK以上であるようなところ が存在すれば,不安定度x以下にできることが分かる. ? これで二分探索したらよさそう. ? 任意の正方形領域に含まれる点の数を高速に計算 するため,予め二次元累積和を計算しておく.
- 19. D問題 考察 ? 次にチームの不安定度の最小値mを達成する組み 合わせ数を求めたい. ? 単純に全ての領域に対してKコを選ぶ組み合わせの 数を計算するのは,重複が発生しダメ. ? ある点を角(x,y)と決めたときに,その点を角にした 正方形(左上(x,y)右下(x+m,y+m))のときにしか達成 できないような選び方を計算することで重複なく数え られる ? そのような選び方は2パターンある(次スライド)
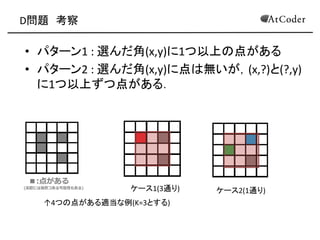
- 20. D問題 考察 ? パターン1 : 選んだ角(x,y)に1つ以上の点がある ? パターン2 : 選んだ角(x,y)に点は無いが,(x,?)と(?,y) に1つ以上ずつ点がある. ケース1(3通り) ケース2(1通り) ↑4つの点がある適当な例(K=3とする)
- 21. D問題 考察 ? 説明のために – 正方形領域の全ての点の数をall – 角(x,y)の点をcorner – 左端領域の点と上端領域の点の数をleft,top と表す [パターン1の個数] – nCr(all,K) - nCr(all-corner,K) [パターン2の個数] – nCr(number-corner,K) - nCr(number-corner-top,K) - ncr(number-corner-left,K) + nCr(number-corner-(top+left),K) corner以外でKコ cornerとtop以外でKコ cornerとleft以外でKコ cornerとleftとtop以外でKコ (引きすぎた分を足す,包除原理)
- 22. D問題 アルゴリズム ? モンスターのパラメータの最大値をM(<=3000)とする ? Nコの点をプロットする → O(N) ? 二次元累積和を計算しておく → O(M^2) ? チームの不安定度の最小値mを二分探索で求める → 累積和を用いて O(M^2 log M) ? 組み合わせ数を求める → O(M^2) nCrの計算は予め0≦k≦Nについてk!と(k!の逆元)をmod 10^9+7で計算しておく ことでO(1) ? 全体として O(M^2 log M)










![C問題 アルゴリズム
? 時刻 i それぞれに対し、(i 以降で最大でいくつ取れ
るか?,最大の取り方のうち、次に取れる最小の仕事
の番号はいくつか?) のペアが更新すればできそう
– i から始めるとき、次に取る区間は辞書順最小の条件か
ら、(最大の取り方のうち、次に取れる最小の仕事の番号)
となるから
? このペアを dp[i] とおく
2015/1/3 13](https://image.slidesharecdn.com/arc032-150103072940-conversion-gate02/85/AtCoder-Regular-Contest-032-13-320.jpg)
![C問題 アルゴリズム
? dp[i] を求めるとき、
– 時刻 i から始まる区間を使うとき、時刻 i から始まり、b で終わ
る番号idの区間を使う場合、 (b以降で取れる区間の最大数
+1,id) が候補
– 時刻 i から始まる区間を使わないとき、(時刻 i+1 以降で取れる
区間の最大数, そのうちの最小の仕事の番号) が候補
– 以上のペアから、取れる区間の最大数で比較し、多いものを選
ぶ。それが同じなら、次に取る仕事の番号が小さいものを選ぶ。
? 番号が同じ区間はないので、このペアが同じになることは無い
? 以上のことから、dp[i] の更新に必要なのは i+1 以降の
dpの情報
? よって、dp[i] を後ろから更新していけばよい
2015/1/3 14](https://image.slidesharecdn.com/arc032-150103072940-conversion-gate02/85/AtCoder-Regular-Contest-032-14-320.jpg)
![C問題 アルゴリズム
? dp[0] が求まったら、0 以降で取れる区間の最大数
が1つ目の答え。
? 復元するときは、今の時刻以降で最大の取り方のう
ち最小の番号の区間をとり続けていく
– dp のペアの2番目の情報にこれがそのまま入っている
– 最初に “今の時刻”=0 とし、次に取る区間を答えに追加
し、”今の時刻”を最後に取った区間の終端に更新
– これを、取れる区間が無くなるまで繰り返す
? 合計でもO(N)!
2015/1/3 15](https://image.slidesharecdn.com/arc032-150103072940-conversion-gate02/85/AtCoder-Regular-Contest-032-15-320.jpg)




![D問題 考察
? 説明のために
– 正方形領域の全ての点の数をall
– 角(x,y)の点をcorner
– 左端領域の点と上端領域の点の数をleft,top
と表す
[パターン1の個数]
– nCr(all,K) - nCr(all-corner,K)
[パターン2の個数]
– nCr(number-corner,K)
- nCr(number-corner-top,K)
- ncr(number-corner-left,K)
+ nCr(number-corner-(top+left),K)
corner以外でKコ
cornerとtop以外でKコ
cornerとleft以外でKコ
cornerとleftとtop以外でKコ
(引きすぎた分を足す,包除原理)](https://image.slidesharecdn.com/arc032-150103072940-conversion-gate02/85/AtCoder-Regular-Contest-032-21-320.jpg)
