![A-数式で表す
● t[i] = i日目の高橋くんの睡眠予定時間
● 3 ≦ i ≦ N なる i のなかで
t[i-2] + t[i-1] + t[i] < K
となる最小の i を、存在するなら求めよ](https://image.slidesharecdn.com/arc036-150404083032-conversion-gate01/85/AtCoder-Regular-Contest-036-4-320.jpg)
![A-解法
● t[i] = i日目の高橋くんの睡眠予定時間
● 3 ≦ i ≦ N なる i のなかで
t[i-2] + t[i-1] + t[i] < K
となる最小の i を、存在するなら求めよ
● N ≦ 100,000なので、iを全通り試しても十分
まにあう
– 満点解法](https://image.slidesharecdn.com/arc036-150404083032-conversion-gate01/85/AtCoder-Regular-Contest-036-5-320.jpg)
![A-注意点
● i = 1, i = 2のときは調べないようにしなければ
ならない
– t[-1]に参照して実行時エラーになりうる
● 不等号に注意
– t[i-2] + t[i-1] + t[i] ≦ K にすると失敗する
– 問題文をよく読みましょう](https://image.slidesharecdn.com/arc036-150404083032-conversion-gate01/85/AtCoder-Regular-Contest-036-6-320.jpg)
![部分点解法 2
? dp[i][j] = (場所 i まで調べていて矛盾 (差が ? を上回る状態) がなく、
かつ場所 i から左に伸ばしたときに考えられる差がビット列 j となる
ような 0,1 割り当ての総数) とします。
? 状態遷移は、今見ている場所に 0,1 のどちらが入るかを決めれば次
は一意に定まるので各状態につき O(1) で判定できます。
? このような動的計画法は O(2 ? ?) で実行できます。
? ? が小さいデータセット 2 に関して正解することができます。](https://image.slidesharecdn.com/arc036-150404083032-conversion-gate01/85/AtCoder-Regular-Contest-036-16-320.jpg)
![満点解法
? dp[i][j][k] = (場所 i まで考えて矛盾 (差が ? を上回る状態) がなく、i
から左に伸ばしたときの (0 の個数)-(1 の個数) の最大値が j で最小
値が –k であるようなものの総数) とします。
? このような動的計画法は O(?3) で実行できます。
? このアルゴリズムなら満点を得ることができます。](https://image.slidesharecdn.com/arc036-150404083032-conversion-gate01/85/AtCoder-Regular-Contest-036-18-320.jpg)
AtCoder Regular Contest 036 解説
- 1. AtCoder Regular Contest 036 解説 AtCoder株式会社 2015/4/4 1
- 3. A-問題概要 ● 高橋くんの睡眠予定がN日分与えられる。 ● 連続する3日の睡眠量の合計がKを下回ると高 橋くんは睡眠不足になる。 ● 高橋くんが睡眠不足になるかどうか、なるなら 何日目になるか求めよ。
- 4. A-数式で表す ● t[i] = i日目の高橋くんの睡眠予定時間 ● 3 ≦ i ≦ N なる i のなかで t[i-2] + t[i-1] + t[i] < K となる最小の i を、存在するなら求めよ
- 5. A-解法 ● t[i] = i日目の高橋くんの睡眠予定時間 ● 3 ≦ i ≦ N なる i のなかで t[i-2] + t[i-1] + t[i] < K となる最小の i を、存在するなら求めよ ● N ≦ 100,000なので、iを全通り試しても十分 まにあう – 満点解法
- 6. A-注意点 ● i = 1, i = 2のときは調べないようにしなければ ならない – t[-1]に参照して実行時エラーになりうる ● 不等号に注意 – t[i-2] + t[i-1] + t[i] ≦ K にすると失敗する – 問題文をよく読みましょう
- 7. B 問題 山のデータ
- 8. 概要 ? 長さ ? の数列があります。 ? ? ? ≦ ? ?+1 ≦ ? ≦ ? ? ≧ ? ≧ ? ? となる整数組 (?, ?, ?) のうち、 ? ? ? + 1 の最大値を求めてください。 ? 1 ≦ ? ≦ 300,000 ? 1 ≦ ?? ≦ 1,000,000,000
- 9. 部分点解法 ? すべての整数組 (?, ?, ?) について考えます。 ? 整数組 (?, ?, ?) が実際に山の条件を満たしているかは、O(?) 回の 判定でできます。 ? 考えられる整数組は O(?3 ) 個あるので、全体で O(?4 ) の計算量と なります。
- 10. 考察 ? ? や ? に関して、外側に伸ばせるのに伸ばさないのはもったいない です。 ? 先に ? を固定して、 ? と ? を外側に伸ばせるだけ伸ばすという方針 で O(?2) に減らすことができます。 ? O(?2) よりも高速にするために、さきほどの ? に関して考えてみます。
- 11. 満点解法 ? 先ほどの ? としては、データの両端であるか、? ??1 ≦ ? ? かつ ? ? ≧ ? ?+1 であるような ? だけ考慮すれば良いことが分かります (そうでな い場合、 ? ? 1 あるいは ? + 1 の方がより良い結果になることが分 かります)。 ? このように限定した場合、どの要素も高々定数回しかアクセスされな いので、全体で O(?) となります。
- 12. C 問題 偶然ジェネレータ
- 13. 概要 ? 長さ ? の 0,1 からなる数列があります。 ? ? となっている場所をうまく 0,1 で埋めて、どのように部分列を取って きても 0,1 の個数の差が ? 以下となるようにします。 ? 考えられる総数を 1,000,000,007 で割った余りを求めてください。 ? 1 ≦ ? ≦ 300 ? 1 ≦ ? ≦ ?
- 14. 部分点解法 1 ? すべての 0,1 割り当てを考えます。 ? すべての配置が定まれば、その配置が条件を満たしているかは O(?3) で判定できます。 ? 考えられる個数は 2 ? 個あるので、全体で O(2 ? ?3 ) となります。 ? 1 つめのデータセットに対して正解できます。
- 15. 部分点解法 2 ? 動的計画法を用いて左から順に調べることを考えます。 ? 考えるべき状態数としては、今まで調べた場所と、調べた場所の右 端から左に伸ばしたときに (0 の個数)-(1 の個数) として何が考えら れ、何が考えられないのかという情報です。 ? 後者 (0,1 の差) は、(0 の個数)-(1 の個数)として、 <1 が考えられる>、 <2 が考えられる>、…、 < ? が考えられる>、 <-1 が考えられる>、 <-2 が考えられる>、…、 < ?? が考えられる> という、合計で 2? ビットの 情報を持っていれば表現できます (差 0 は、長さ 0 の列を考えれば 常に存在します)。
- 16. 部分点解法 2 ? dp[i][j] = (場所 i まで調べていて矛盾 (差が ? を上回る状態) がなく、 かつ場所 i から左に伸ばしたときに考えられる差がビット列 j となる ような 0,1 割り当ての総数) とします。 ? 状態遷移は、今見ている場所に 0,1 のどちらが入るかを決めれば次 は一意に定まるので各状態につき O(1) で判定できます。 ? このような動的計画法は O(2 ? ?) で実行できます。 ? ? が小さいデータセット 2 に関して正解することができます。
- 17. 考察 ? すべての状態を考えていても、指数オーダーの計算量となります。 ? (0 の個数)-(1 の個数) の最大値および最小値が一致するもの同士 をまとめて数え上げたいです。 ? 実は最大値および最小値が一致するものをまとめても、特に問題は ありません (なぜなら、差が ? を最初に越えるのは、必ず最大値か 最小値のいずれかであり、かつ状態遷移によってどの状態が考えら れるかは、平行移動 (+ 差が 0) という変化しかないので、最大値と 最小値だけ考慮しておけばよいことになります)。
- 18. 満点解法 ? dp[i][j][k] = (場所 i まで考えて矛盾 (差が ? を上回る状態) がなく、i から左に伸ばしたときの (0 の個数)-(1 の個数) の最大値が j で最小 値が –k であるようなものの総数) とします。 ? このような動的計画法は O(?3) で実行できます。 ? このアルゴリズムなら満点を得ることができます。
- 20. D-問題概要 ● 辺の無いグラフ（頂点数N）がある。 ● 以下の2種類のクエリQ個に答えよ – 頂点x, yの間にdメートルの辺を引く – 頂点xから頂点yへのwalkのなかで偶数メートルのも のがあるか判定せよ ※walkというのは同じ辺を複数回通ることを許 した経路のこと。
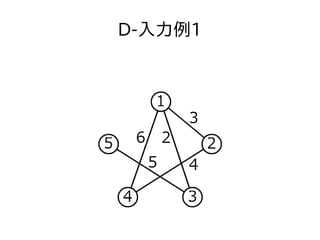
- 21. 顿-入力例1
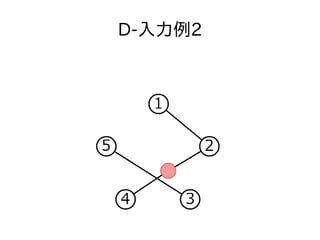
- 27. 顿-入力例2
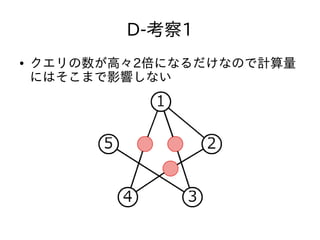
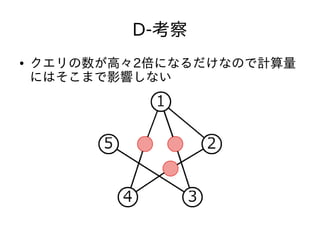
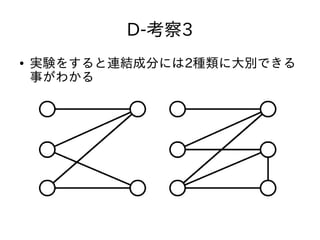
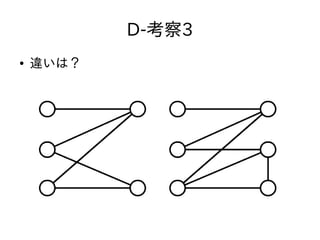
- 33. D-考察3 ● 違いは？
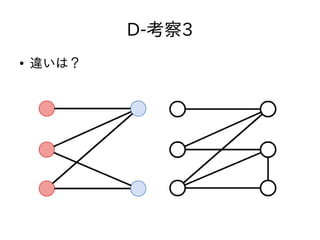
- 34. D-考察3 ● 違いは？
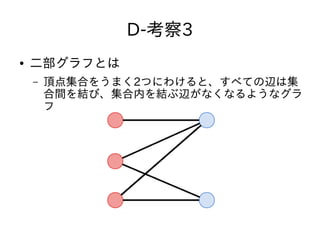
- 35. D-考察3 二部グラフ
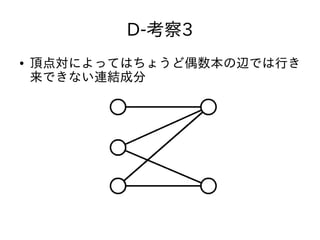
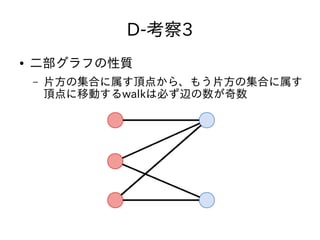
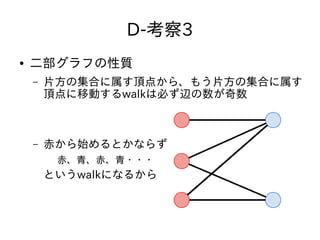
- 38. D-考察3 ● 二部グラフの性質 – 片方の集合に属す頂点から、もう片方の集合に属す 頂点に移動するwalkは必ず辺の数が奇数 – 赤から始めるとかならず 赤、青、赤、青??? というwalkになるから
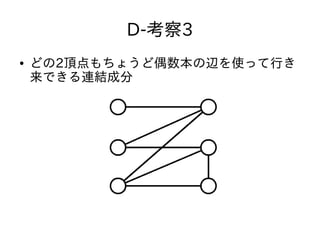
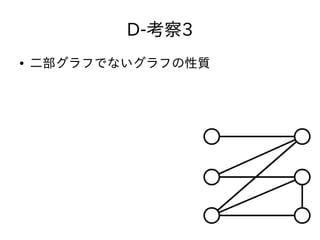
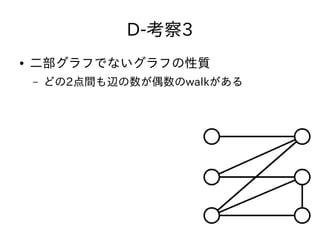
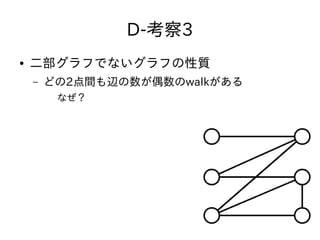
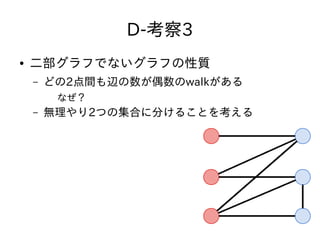
- 42. D-考察3 ● 二部グラフでないグラフの性質 – どの2点間も辺の数が偶数のwalkがある なぜ？ – 无理やり2つの集合に分けることを考える
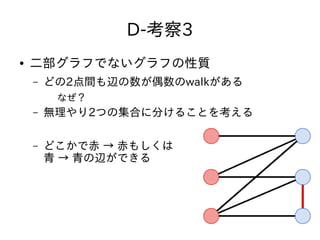
- 43. D-考察3 ● 二部グラフでないグラフの性質 – どの2点間も辺の数が偶数のwalkがある なぜ？ – 无理やり2つの集合に分けることを考える – どこかで赤 → 赤もしくは 青 → 青の辺ができる
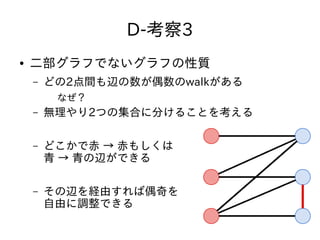
- 44. D-考察3 ● 二部グラフでないグラフの性質 – どの2点間も辺の数が偶数のwalkがある なぜ？ – 无理やり2つの集合に分けることを考える – どこかで赤 → 赤もしくは 青 → 青の辺ができる – その辺を経由すれば偶奇を 自由に調整できる
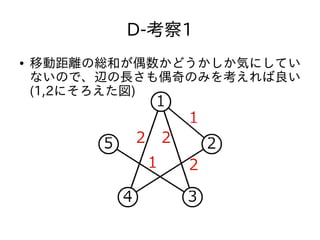
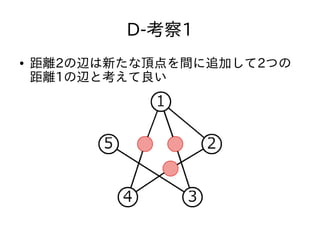
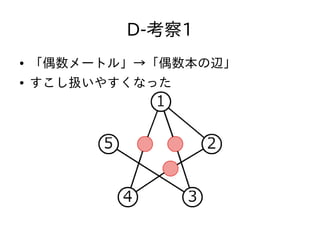
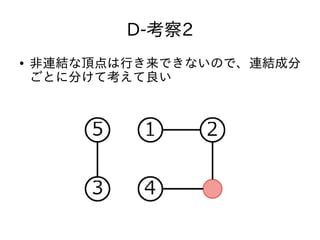
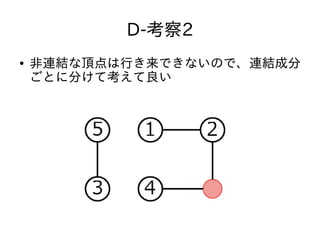
- 45. D-考察まとめ ● グラフの辺の長さをすべて1にすることができ る ● 連結成分ごとに別々に考えて良い ● 連結成分が二部グラフかどうかが鍵になってい る
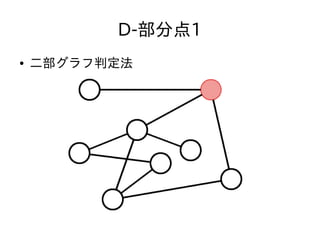
- 46. D-部分点1 ● N,Q ≦ 3,000 ● クエリ毎に毎回質問された頂点が二部グラフか どうか判定しても充分間に合う
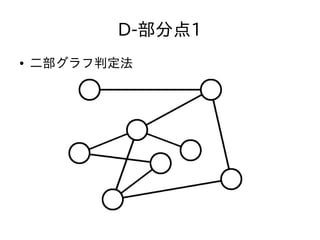
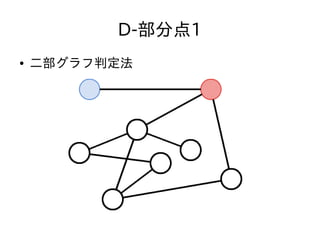
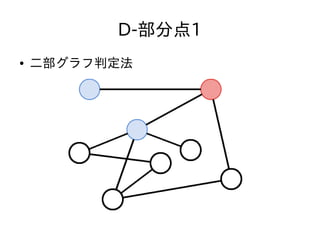
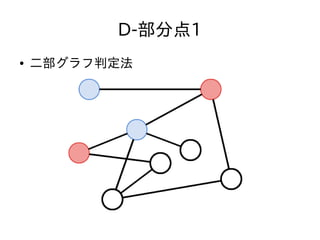
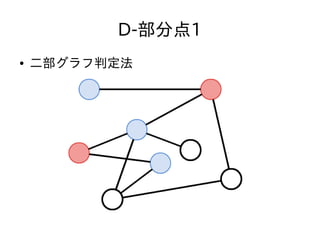
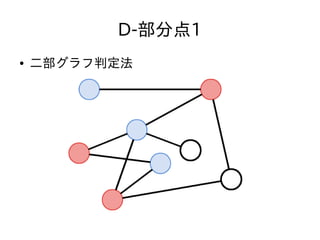
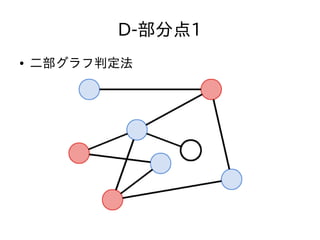
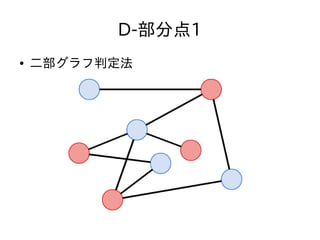
- 47. D-部分点1 ● N,Q ≦ 3,000 ● クエリ毎に毎回質問された頂点が二部グラフか どうか判定しても充分間に合う ● 二部グラフ判定法 – 適当な頂点を赤く塗る – そこから始めて、隣接する頂点の色が異なるように DFSしながら塗っていく – 隣接する頂点の色がおなじになる辺があったら二部 グラフではない。なかったら二部グラフ
- 57. D-部分点1 ● 二部グラフ判定法 – 判定と同時に塗り分けもできる ● まとめ – 頂点X、頂点Yが連結でない NO – 連結で二部グラフでない YES – 連結で二部グラフで同じ色である YES – 連結で二部グラフで違う色である NO ● 30点獲得
- 59. D-考察4 ● 辺は増える一方なので、一度でも二部グラフの 異なる色となった2頂点はずっと異なる色のま まである – 毎回DFSして塗り分けするのは無駄が多い ● 辺による连结のパターンを考えてみる
- 60. D-考察4 ● パターン1 – 連結成分の少なくとも一方が二部グラフでない辺 – 二部グラフでないものになにを追加しても二部グラ フではなくなる
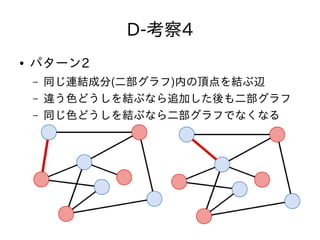
- 61. D-考察4 ● パターン2 – 同じ連結成分(二部グラフ)内の頂点を結ぶ辺 – 違う色どうしを結ぶなら追加した後も二部グラフ – 同じ色どうしを結ぶなら二部グラフでなくなる
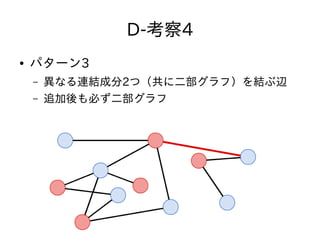
- 62. D-考察4 ● パターン3 – 異なる連結成分2つ（共に二部グラフ）を結ぶ辺 – 追加后も必ず二部グラフ
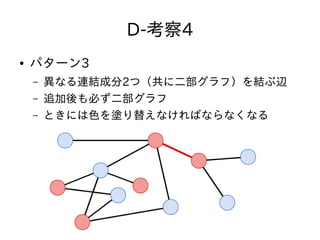
- 63. D-考察4 ● パターン3 – 異なる連結成分2つ（共に二部グラフ）を結ぶ辺 – 追加后も必ず二部グラフ – ときには色を塗り替えなければならなくなる
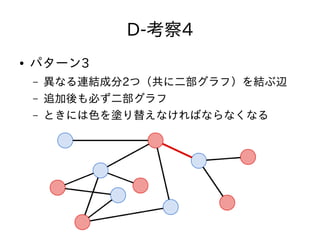
- 64. D-考察4 ● パターン3 – 異なる連結成分2つ（共に二部グラフ）を結ぶ辺 – 追加后も必ず二部グラフ – ときには色を塗り替えなければならなくなる
- 65. D-考察4 ● パターン1, 2の処理は簡単そう ● パターン3をどうするか？ – 具体的には色の塗り直しをどうするか？
- 66. D-考察4 ● パターン1, 2の処理は簡単そう ● パターン3をどうするか？ – 具体的には色の塗り直しをどうするか？ 解法1:マージテク 解法2:縮約
- 67. D-満点解法1 ● 各頂点について – どの連結成分に属すか？ – 何色に塗られているか？ ● 各連結成分について – 二部グラフか？
- 68. D-満点解法1 ● 各頂点について – どの連結成分に属すか？ UnionFindを使用 – 何色に塗られているか？ 配列で管理 ● 各連結成分について – 二部グラフか？ 配列で管理
- 69. D-満点解法1 ● パターン1, 2の辺については適当に処理する – 変更する情報は定数個なので、あまり計算量に影響 しない ● パターン3の塗り直しをどうするか – 頂点数が少ない方を塗り直すようにすれば良い – いわゆる「マージテク」 – どの頂点も塗り直されるタイミングで自分が属する 連結成分の大きさが2倍以上になる ● たかだかlogN回しか塗り直さない
- 70. D-満点解法1 ● 注意 – DFSの計算量はO(頂点数)ではなくてO(辺の数) – それならば頂点数ではなくて辺の数の大小でマージ テクをするべきでは？ ● 結論から言うと問題ない ● 先と同様の論法で各辺がDFSで走査される回数も O(logN)程度 – 二部グラフかどうかわかっているので、全域木の辺 のみを管理するという手もある
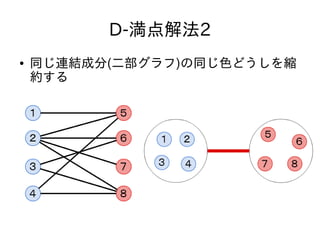
- 72. D-満点解法2 ● パターン1,2は満点解法1と同様 ● パターン3が問題 – 缩约のおかげで涂り替えが定数回で済む
- 73. D-満点解法まとめ ● 満点解法1 – マージテクを使っていちいち色を塗り直す – O(Q log N) ● 満点解法2 – 縮約によって塗り直す色を定数個に減らす – O(Q α(N)) ※α(N)はアッカーマン関数の逆関数
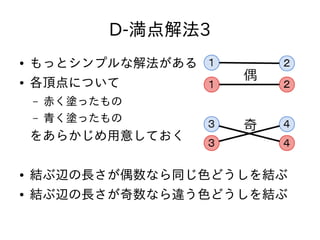
- 74. D-満点解法3 ● もっとシンプルな解法がある ● 各頂点について – 赤く塗ったもの – 青く塗ったもの をあらかじめ用意しておく
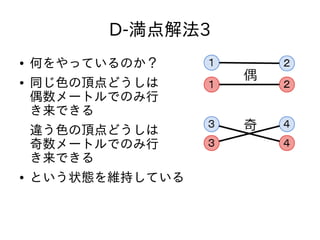
- 75. D-満点解法3 ● もっとシンプルな解法がある ● 各頂点について – 赤く塗ったもの – 青く塗ったもの をあらかじめ用意しておく ● 結ぶ辺の長さが偶数なら同じ色どうしを結ぶ ● 結ぶ辺の長さが奇数なら違う色どうしを結ぶ
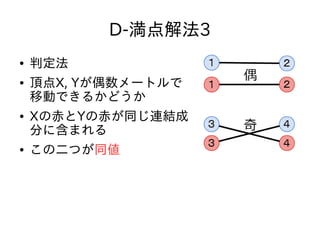
- 77. D-満点解法3 ● 判定法 ● 頂点X, Yが偶数メートルで 移動できるかどうか ● Xの赤とYの赤が同じ連結成 分に含まれる ● この二つが同値
- 78. D-満点解法3 ● 実装 – 辺を結ぶことと、同じ連結成分に属するかを判定す るだけ ● ただのUnionFind ● 極めて軽実装 ● 計算量 – O(Qα(N))