![B問題 満点解法
? 各教室がいくつの区間に被覆されてるか分かれば，
ある教室を除いても全ての教室が掃除できる
?区間内の全ての教室が2つ以上の区間に被覆されている
?区間内に，被覆数が1の教室が含まれない
? 教室iの被覆数が1ならX[i]=1，そうでないならX[i]=0を記録した
配列Xに対し累積和配列Sを生成すると，ある区間に含まれる
被覆数1の教室の個数がO(1)で計算できるようになる
? 各区間に対してO(1)でそれが解に含まれるかどうかが判定でき
るようになり，判定にかかる計算量はO(M)となった．
? 全体の時間計算量,空間計算量は O(N+M) となり満点
5](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-10-320.jpg)
![B問題 アルゴリズム動作例
6
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-11-320.jpg)
![B問題 アルゴリズム動作例
7
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-12-320.jpg)
![B問題 アルゴリズム動作例
8
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-13-320.jpg)
![B問題 アルゴリズム動作例
9
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-14-320.jpg)
![B問題 アルゴリズム動作例
10
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-15-320.jpg)
![B問題 アルゴリズム動作例
11
? いもす法を行う 入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-16-320.jpg)
![B問題 アルゴリズム動作例
12
? いもす法を行う
→の方向に累積和を取るとこうなる
入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-17-320.jpg)
![B問題 アルゴリズム動作例
13
? 被覆数が1の部分だけに着目
? 満点解法で述べた配列Xを生成
入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-18-320.jpg)
![B問題 アルゴリズム動作例
14
? 被覆数が1の部分だけに着目
再度→方向に累積和を取り
満点解法で述べた配列Sを生成
入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-19-320.jpg)
![B問題 アルゴリズム動作例
15
? 後は各区間について調べる
? 被覆数1の教室を含むかどうか判定
? [1,4] → S[4] – S[0](=0とする) = 4なので×
? [5,5] → S[5] – S[4] = 0なので○
? [6,8] → S[8] – S[5] = 2なので×
? [9,10] → S[10] – S[8] = 2なので×
? [5,6] → S[6] – S[4] = 0なので○
入力例
N=5,M=10
[1,4]
[5,5]
[5,6]
[6,8]
[9,10]](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-20-320.jpg)
![C問題 解法
? 適当な頂点からdfsを行い，根からの頂点iまでの単純パス
のxor値x[i]が出現した回数をハッシュや平衡二分木(C++の
map等)を用いて記録していく．
? 各x[i]が出現した回数を加算する前に，X xor x[i] という値
が今までに出現した回数を答えに加算していけば良い．
? 時間?空間計算量はハッシュを用いた場合 O(N)
[コーナーケース]
? X=0のとき，(x,x)を組として数えないように気をつけるこ
と(求めるのはa<bとなる組の個数です)．
? 32bit整数だとオーバーフローします．
4](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-24-320.jpg)
![関节点列挙
? これがわかると何が嬉しいの？
? 実は、関節点であるかは以下の条件を満たすかで判
定できる
? (根)次数が2以上
? (根以外, vとする)子uの中にlow[u] ord[v]なる
頂点が存在する](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-57-320.jpg)
![関节点列挙
? これがわかると何が嬉しいの？
? 実は、関節点であるかは以下の条件を満たすかで判
定できる
? (根)次数が2以上
? (根以外, vとする)子uの中にlow[u] ord[v]なる
頂点が存在する
これはdfs木の性質から明らか](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-58-320.jpg)
![関节点列挙
? これがわかると何が嬉しいの？
? 実は、関節点であるかは以下の条件を満たすかで判
定できる
? (根)次数が2以上
? (根以外, vとする)子uの中にlow[u] ord[v]なる
頂点が存在する
こっちは？](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-59-320.jpg)
![関节点列挙
? ordとlowは全頂点まとめてO(V+E)で計算可能
? この条件下で関節点とは以下の条件を満たす頂点
? (根)次数が2以上
? (根以外, vとする)子uの中にlow[u] ord[v]なる頂点が存在する
? これらもO(V+E)で計算可能
? さらに、これらを満たす子uのなかで(uの部分木のサイズ)が奇数にな
るものがあったらNG
? まとめてO(V+E)](https://image.slidesharecdn.com/arc045-151010133906-lva1-app6891/85/AtCoder-Regular-Contest-045-72-320.jpg)
AtCoder Regular Contest 045 解説
- 1. AtCoder Regular Contest 045 解説 AtCoder株式会社 10/10/15
- 3. 問題概要 ? 文字列が与えられる ? Left → < ? Right → > ? AtCoder → A ? と置換して出力
- 4. 解法(C++) ? getline等の関数を使うと1行まるまる読み込めます ? cin, scanfで読み込む場合は空白文字に注意してく ださい ? 空白後の1文字を見て、Lなら<、Rなら>、AならA を出力し、そのあと次の空白まで進む。などの解法 が考えられます
- 5. 解法 ? 文字列を扱う高級な関数を使うと楽です ? たとえばpythonならreplace('AtCoder', 'A')で AtCoderを全部Aにできます ? プロコンにおいてC++しか使わない人は多いと思い ますが、他にpython,ruby等の文字列処理のライブ ラリが充実している言語を1個は使えるとよいです
- 6. ?AtCoder Inc. All rights reserved. B問題 ドキドキデート大作戦高橋君(解説スライド:三上) 1. 問題概要 2. 考察 3. 解法 4. アルゴリズム動作例 1
- 7. B問題 問題概要 ? Nコの教室があり，全ての教室を掃除したい ? 担当すると掃除しなければならない区間(掃除区間)がMコ 与えられる(これは重なることがある) ? ある区間iを掃除しなかったとしても，全ての教室が問題 なく掃除されているような区間iを全て列挙せよ． ? Mコの区間を全て使った場合に全ての教室が掃除できる ことは保証されている． ? 1≦N≦10^6 ? 1≦M≦10^5 2
- 8. B問題 考察 ? まず，各教室がいくつの区間に被覆されているかを求めておくと 見通しがよくなる． ? これはimos法(※)を用いて時間計算量 O(N+M) で達成可能 ※ http://www.slideshare.net/chokudai/abc014 (P3参照) ? 各教室がいくつの区間に被覆されてるか分かれば， ある教室を除いても全ての教室が掃除できる ?区間内の全ての教室が2つ以上の区間に被覆されている 3
- 9. B問題 部分点解法(30点) ? 追加制約 – 任意の教室 i(1≦i≦N) について，その教室を含む掃除区間の数は高々 2 つである ? この制約上では，全ての区間について，区間内の全ての教室 の被覆数を繰り返し文で愚直にチェックして，それらの最小値が 2以上ならその区間を解の候補に入れるというアルゴリズムで 正解する． ? 理由は，for文で愚直にチェックしたところで，2回より多く同じ教 室を見ることはないので，高々 2N 回しかループしないから ? 別解もたくさんある – 各教室について，その教室を被覆している区間の番号の列 を持つ配列を用意する等 4
- 10. B問題 満点解法 ? 各教室がいくつの区間に被覆されてるか分かれば， ある教室を除いても全ての教室が掃除できる ?区間内の全ての教室が2つ以上の区間に被覆されている ?区間内に，被覆数が1の教室が含まれない ? 教室iの被覆数が1ならX[i]=1，そうでないならX[i]=0を記録した 配列Xに対し累積和配列Sを生成すると，ある区間に含まれる 被覆数1の教室の個数がO(1)で計算できるようになる ? 各区間に対してO(1)でそれが解に含まれるかどうかが判定でき るようになり，判定にかかる計算量はO(M)となった． ? 全体の時間計算量,空間計算量は O(N+M) となり満点 5
- 11. B問題 アルゴリズム動作例 6 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 12. B問題 アルゴリズム動作例 7 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 13. B問題 アルゴリズム動作例 8 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 14. B問題 アルゴリズム動作例 9 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 15. B問題 アルゴリズム動作例 10 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 16. B問題 アルゴリズム動作例 11 ? いもす法を行う 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 18. B問題 アルゴリズム動作例 13 ? 被覆数が1の部分だけに着目 ? 満点解法で述べた配列Xを生成 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 20. B問題 アルゴリズム動作例 15 ? 後は各区間について調べる ? 被覆数1の教室を含むかどうか判定 ? [1,4] → S[4] – S[0](=0とする) = 4なので× ? [5,5] → S[5] – S[4] = 0なので○ ? [6,8] → S[8] – S[5] = 2なので× ? [9,10] → S[10] – S[8] = 2なので× ? [5,6] → S[6] – S[4] = 0なので○ 入力例 N=5,M=10 [1,4] [5,5] [5,6] [6,8] [9,10]
- 21. ?AtCoder Inc. All rights reserved. C問題 エックスオア多橋君(解説スライド:三上) 1. 問題概要 2. 考察 3. 解法 4. アルゴリズム動作例 1
- 22. C問題 問題概要 ? 辺に非負整数の重みがついたN頂点の木が与えられる． ? 整数Xも与えられる． ? aからbの単純パス上の辺の重みのxor和がXになるような (a,b)の組(a<b)の個数を求めよ． ? 1≦N≦10^5 ? 0≦X,辺のコスト≦10^9 2
- 23. C問題 考察 ? 適当な頂点xを根に行ったdfsで，根からの経路の総和 xor を持っておくと嬉しい．なぜなら， パスa→bのxor値 = (a→xのxor 値) xor (x→bのxor 値) ? が成り立つから． ? 理由は a→x→bという経路の中で2回通る辺のコストは打 ち消し合うから 3
- 24. C問題 解法 ? 適当な頂点からdfsを行い，根からの頂点iまでの単純パス のxor値x[i]が出現した回数をハッシュや平衡二分木(C++の map等)を用いて記録していく． ? 各x[i]が出現した回数を加算する前に，X xor x[i] という値 が今までに出現した回数を答えに加算していけば良い． ? 時間?空間計算量はハッシュを用いた場合 O(N) [コーナーケース] ? X=0のとき，(x,x)を組として数えないように気をつけるこ と(求めるのはa<bとなる組の個数です)． ? 32bit整数だとオーバーフローします． 4
- 25. C問題 コーナーケース ? X=0のとき，(x,x)を組として数えないように気をつけるこ と(a<bとなる組の個数です) ? 答えは32bit整数だとオーバーフローします． ? 別解はいくつかあります – データ構造をマージする一般的なテク（平衡二分木を マージしていくとO(nlog^2n)の時間計算量等で達成可 能） – オイラーツアーを構築して列の問題に帰着させる（本 質的にはこのスライドで述べた方法と同じ） 5
- 27. 問題概要 ? 点が2N+1個与えられる ? x座標かy座標が同じ点はマッチング出来る ? この点以外の点で完全マッチングが作れる かどう かを全ての点について判定 ? N 100,000
- 30. 例 ? 以下のグラフで考える
- 42. 考察 ? 最初の状態で連結成分が1個だけの場合を考えれば よい ? 奇数の連結成分が複数あったら全部NG ? 偶数の連結成分はなかったものと考えて良い ? 点を削除して連結成分が増える、かつ増えた連結成 分のうち点が奇数個のものがある場合のみNG
- 43. 考察 ? 点を削除した結果連結成分が増えるような点を関節 点と呼ぶ。これはO(V + E)で列挙可能(後述) ? 消した結果出来た連結成分のサイズが奇数かどうか の判定も実はまとめてできる(後述) ? ただ普通にグラフを作るとEは最悪θ(V^2)になる ので、減らさなくてはいけない
- 44. 考察 ? O(V^2)本の辺を全て張る必要はない ? もし一つの点からたくさん辺が伸びている場合は、 4方向毎に2番目に近い点までのみに辺を貼ればよ い ? これで辺の本数はO(V)、これであとはO(V+E)で関 節点列挙すれば良い
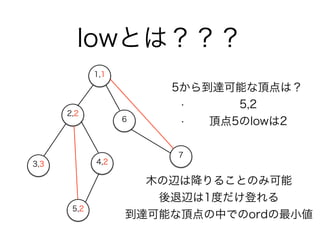
- 45. 関节点列挙 ? lowlinkという方法で列挙できます ? dfs木を作り、頂点毎にordとlowというパラメー ターを計算する ? ordはdfs木上での行きがけ順序 ? lowは木の辺は降りることのみ可能、ただし後退 辺を最後に1度だけ登っても良い?という条件下 での到達可能な頂点の中でのordの最小値
- 46. 関节点列挙
- 57. 関节点列挙 ? これがわかると何が嬉しいの？ ? 実は、関節点であるかは以下の条件を満たすかで判 定できる ? (根)次数が2以上 ? (根以外, vとする)子uの中にlow[u] ord[v]なる 頂点が存在する
- 58. 関节点列挙 ? これがわかると何が嬉しいの？ ? 実は、関節点であるかは以下の条件を満たすかで判 定できる ? (根)次数が2以上 ? (根以外, vとする)子uの中にlow[u] ord[v]なる 頂点が存在する これはdfs木の性質から明らか
- 59. 関节点列挙 ? これがわかると何が嬉しいの？ ? 実は、関節点であるかは以下の条件を満たすかで判 定できる ? (根)次数が2以上 ? (根以外, vとする)子uの中にlow[u] ord[v]なる 頂点が存在する こっちは？
- 62. 関节点列挙 消してみる
- 68. 関节点列挙 v p u uから木を降りて、 後退辺を1回登ってpかpの親に行ければ よい どういう後退辺があったら分離しないか？ uの部分木のどこかと、 pとpの親のうちどこかをつなぐような 後退辺
- 71. 関节点列挙 v p u つまり、low(u) < ord(v)か判定すれば良い 逆にlow(u) ord(v)なる子があったら関節点 → low(u)! uから木を降り後退辺を1回登っていける 頂点 このなかでもっとも上のものは？ uから木を降りて、 後退辺を1回登ってpかpの親に行ければ よい
- 72. 関节点列挙 ? ordとlowは全頂点まとめてO(V+E)で計算可能 ? この条件下で関節点とは以下の条件を満たす頂点 ? (根)次数が2以上 ? (根以外, vとする)子uの中にlow[u] ord[v]なる頂点が存在する ? これらもO(V+E)で計算可能 ? さらに、これらを満たす子uのなかで(uの部分木のサイズ)が奇数にな るものがあったらNG ? まとめてO(V+E)
- 73. lowを求める方法 ? 具体的にlowはどう求めればいいのか？ ? 普通にdfsをする ? 今頂点uにいて、辺(u, v)に注目してるとする ? vをもう通ったならlow(u)=min(low(u), ord(v)) ? 通って無いならlow(u)=min(low(u), low(v)) ? これだけで求められる