Area of Polygons_Composite Figures_.pptx
- 1. MATHEMATICS THIRD QUARTER LUIS V. SALENGA
- 2. LECTURE 3.6 Finding the Area of a Figure
- 3. Content Standard: ’éĘ Demonstrates understanding of rate and speed, and of area and surface area of plane and solid/space figures. Performance Standard: ’éĘ Apply knowledge of speed, area, and surface area of plane and solid/space figures in mathematical problems and real-life situations. Learning Competency: ’éĘ Finds the area of composite figures formed by any two or more of the following: triangle, square, rectangle, circle, and semi-circle. Code: 6ME-IIIh-89 LEARNING OBJECTIVES
- 5. Click Me ’üŖ 1 2 3 4 5 6 7 8 9 10
- 6. 4 Pics in a Word 1 Back Next TIME
- 7. 4 Pics in a Word 1 Back Next DISTANCE
- 8. 4 Pics in a Word 1 Back Menu SPEED
- 9. Guess the Shapes 2 Back Menu Triangle Square Rectangle Circle Semi-circle
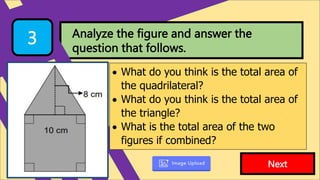
- 10. Analyze the figure and answer the question that follows. 3 Next ’éĘ What do you think is the total area of the quadrilateral? ’éĘ What do you think is the total area of the triangle? ’éĘ What is the total area of the two figures if combined?
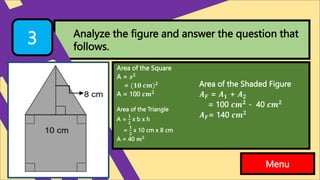
- 11. Analyze the figure and answer the question that follows. 3 Menu Area of the Square A = ØÆöØ¤É = (ؤÅØ¤Ä ØÆäØÆÄ)Ø¤É A = 100 ØÆäØÆÄØ¤É Area of the Triangle A = Ø¤Å Ø¤É x b x h = Ø¤Å Ø¤É x 10 cm x 8 cm A = 40 ØÆÄØ¤É Area of the Shaded Figure Øæ©ØæŁ = Øæ©Ø¤Å + Øæ©Ø¤É = 100 ØÆäØÆÄØ¤É - 40 ØÆäØÆÄØ¤É Øæ©ØæŁ= 140 ØÆäØÆÄؤÉ
- 12. Find the area of the Square. 4 Next Area of the Square A = S X S = 12 m x 12 m A = 144 ØÆÄؤÉ
- 13. Find the area of the Rectangle. 4 Next Area of the Rectangle A = l x w = 2 cm x 1 cm A = 2 ØÆäØÆÄØ¤É Length = 2 cm Width = 1 cm
- 14. Find the area of the Triangle. 4 Next Area of the Triangle A = Ø¤Å Ø¤É x b x h = Ø¤Å Ø¤É x 2 m x 3 m A = 3 ØÆÄØ¤É 3 m 2 m
- 15. Find the area of the Circle. 4 Menu Area of the Circle A = ŽĆ x r x r = 3.14 x 2 m x 2 m A = 12.56 ØÆÄØ¤É r =2 m
- 16. What is the formula for finding the Area of a Square? Rectangle? Triangle? Circle? 5 Next A. A = S X S B. A = l x w C. A = (l X 2) + (w x 2) D. A = Ø¤Å Ø¤É x b x h E. A = ŽĆ x r x r
- 17. What does the symbol ŌĆ£ŽĆŌĆØ represent? 5 Next A. radius B. circle C. pi D. Semi-circle
- 18. What are the similarities and differences of square and rectangle? 5 Next Similarities: 1. They are both quadrilaterals. 2. They have 4 right angles 3. 2 opposite sides are parallel. Differences: 1. Square have 4 equal sides 2. Rectangle have 2 equal sides
- 19. What is your sole observation in putting a unit on the result after finding the area? 5 Next For writing the unit of an ŌĆ£AreaŌĆØ it must always have an exponent of 2. Example: ØÆÄؤÉ, cØÆÄؤÉ, ØÆćØÆĢؤÉ, ØÆŖØÆÅØ¤É Or you can also write it in word like; Square meter, Square Centimeter, Square feet, Square inches
- 20. Integration 5 Menu 1. Social and Cultural Integration: ’éĘ Why is it important to learn how to find the area? ’éĘ How can this help you in determining the area of our house, lot, or cultural heritage? 2. Integration (Subject-Orientation): ŌĆó In what subject you can use in finding the area of a figure?
- 21. LetŌĆÖs Discuss! 6 Next Area of the Rectangle Øæ©Ø¤Å = l x w = 12 ft x 7 ft Øæ©Ø¤Å= 84 ØÆćØÆĢØ¤É Area of the Rectangle Øæ©Ø¤É = l x w = 8 ft x 3 ft. Øæ©Ø¤É= 24 ØÆćØÆĢØ¤É Area of the Shaded Figure Øæ©ØæŁ = Øæ©Ø¤Å - Øæ©Ø¤É = 84 ØÆćØÆĢØ¤É - 24 ØÆćØÆĢØ¤É Øæ©ØæŁ= 60 ØÆćØÆĢØ¤É 60 ØÆćØÆĢؤÉ
- 22. LetŌĆÖs Discuss! 6 Next Area of the Circle A = ŽĆ x r x r = 3.14 x 7 in x 7 in A = 153.86 ØÆŖØÆÅØ¤É Area of the Rectangle A = l x w = 11 in x 3 in A = 33 ØÆŖØÆÅØ¤É Area of the Shaded Figure Øæ©ØæŁ = Øæ©Ø¤Å - Øæ©Ø¤É = 153.86 ØÆŖØÆÅØ¤É - 33 ØÆŖØÆÅØ¤É Øæ©ØæŁ= 120.86 ØÆŖØÆÅØ¤É 120.86 ØÆŖØÆÅؤÉ
- 23. LetŌĆÖs Discuss! 6 Menu Area of the Triangle A = Ø¤Å Ø¤É x b x h = Ø¤Å Ø¤É x 6 m x 7 m A = 21 ØÆÄØ¤É Area of the Rectangle A = l x w = 4 m x 2 m A = 8 ØÆÄØ¤É Area of the Shaded Figure Øæ©ØæŁ = Øæ©Ø¤Å - Øæ©Ø¤É = 21 ØÆÄØ¤É - 8 ØÆÄØ¤É Øæ©ØæŁ= 13 ØÆÄØ¤É 13 ØÆÄؤÉ
- 24. LetŌĆÖs Practice! 7 Menu Area of the Rectangle Øæ©Ø¤Å = l x w = 20 cm x 15 cm Øæ©Ø¤Å= 300 ØÆäØÆÄØ¤É Area of the 2 Squares Øæ©Ø¤É = 2s x 2s = 2(2cm) x 2(2 cm) = 4 cm x 4 cm Øæ©Ø¤É= 16 ØÆäØÆÄØ¤É Total Area of the Figure Øæ©ØæŁ = Øæ©Ø¤Å + Øæ©Ø¤É = 300 ØÆäØÆÄØ¤É + 16 ØÆäØÆÄØ¤É Øæ©ØæŁ= 316 ØÆäØÆÄØ¤É 316 ØÆäØÆÄؤÉ
- 25. LetŌĆÖs Try! 8 Menu Area of the Circle Øæ©Ø¤Å = ŽĆ x r x r = 3.14 x 4 in x 4 in Øæ©Ø¤Å = 50.24 ØÆŖØÆÅØ¤É Area of the Circle Øæ©Ø¤É = ŽĆ x r x r = 3.14 x 2 in x 2 in Øæ©Ø¤É = 12.56 ØÆŖØÆÅØ¤É Total Area of the Shaded Region Øæ©ØæŁ = Øæ©Ø¤Å + Øæ©Ø¤É = 50.24 ØÆŖØÆÅØ¤É + 12.56 ØÆŖØÆÅØ¤É Øæ©ØæŁ= 37.68 ØÆŖØÆÅؤÉ
- 26. Summary/Reflection 9 Menu In summary, what is the importance of learning how to get the area of a space or figure?
- 27. Enrichment/Enhancement/Assignment 10 Next Look for an object and by using a ruler get the measurement and find its area.