ºÝºÝߣ

ºÝºÝߣShare a Scribd company logo

Artificial neural netwoks2

•Download as PPT, PDF•
•
Y
yosser atassi

This document provides a 3-paragraph summary of an artificial neural networks lecture: The lecture discusses perceptrons and how they can be used to classify linearly separable and non-linearly separable data. Perceptrons use a learning algorithm to update their weights to correctly classify input patterns. However, perceptrons cannot solve problems like the XOR function that require more complex decision boundaries. The document provides an example of the XOR problem that perceptrons cannot solve on their own. The document then introduces Adaline learning algorithms. Adalines are adaptive linear neurons that can learn weight values using a learning rule to minimize the mean square error between the actual network output and the target output. An exercise is provided to walk through an

1 of 29
Download to read offline
Artificial Neural Netwoks Dr. Yosser ATASSI Lecture 2
Perceptron
Perceptron
Perceptron x xo x x: class I (y = 1) o: class II (y = -1) x oo o x: class I (y = 1) o: class II (y = -1)
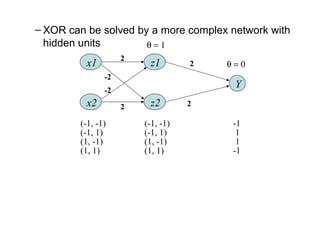
• Examples of linearly inseparable classes - Logical XOR (exclusive OR) function patterns (bipolar) decision boundary x1 x2 y -1 -1 -1 -1 1 1 1 -1 1 1 1 -1 No line can separate these two classes, as can be seen from the fact that the following linear inequality system has no solution because we have b < 0 from (1) + (4), and b >= 0 from (2) + (3), which is a contradiction o xo x x: class I (y = 1) o: class II (y = -1)      <++ ≥−+ ≥+− <−− (4) (3) (2) (1) 0 0 0 0 21 21 21 21 wwb wwb wwb wwb
– XOR can be solved by a more complex network with hidden units Y z2 z1x1 x2 2 2 2 2 -2 -2 θ = 1 θ = 0 (-1, -1) (-1, -1) -1 (-1, 1) (-1, 1) 1 (1, -1) (1, -1) 1 (1, 1) (1, 1) -1
Perceptron Learning
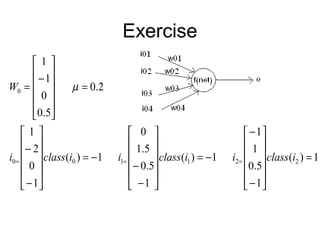
• Perceptron learning algorithm Step 0. Initialization: wk = 0, k = 1 to n Step 1. While stop condition is false do steps 2-5 Step 2. For each of the training sample ij: class(ij) do steps 3 -5 Step 3. compute net= w* ij Step 4. compute o=f(net) Step 5. If o != class(ij) wk := wk + µ ∗ ij * class(ij), k = 1 to n Notes: - Learning occurs only when a sample has o != class(ij) - Two loops, a completion of the inner loop (each sample is used once) is called an epoch Stop condition - When no weight is changed in the current epoch, or - When pre-determined number of epochs is reached
Exercise 1)( 1 5.0 1 1 1)( 1 5.0 5.1 0 1)( 1 0 2 1 5.0 0 1 1 221100 0 =             − − −=             − − −=             − − 0.2=             − = === iclassiiclassiiclassi W µ
[ ] [ ] 12 1 1 111 1 00010 0 000 1 6.1 1 5.0 5.1 0 7.006.08.0 * 7.0 0 6.0 8.0 1 0 2 1 *1*2.0 5.0 0 1 1 *)(1 5.25.0021 1 0 2 1 5.0011 * WW o net iWnet W iiclassWWo net iWnet T T = −= −=             − −= =             − =             − − −+             − = ∗+=+= =−++=             − − −= = µ
[ ] [ ] 5.29.0 1 0 2 1 5.01.04.06.0 5.0 1.0 4.0 6.0 1 5.0 1 1 *2.0 7.0 0 6.0 8.0 1)(1 1.2 1 5.0 1 1 7.006.08.0 * 3 3 22 2 222 <=             − − −=             − =             − − +             − = =≠−= −=             − − −= = net onVerificati W iclasso net iWnet T
Notes Informal justification: Consider o = 1 and class(ij) = -1 – To move o toward class(ij), w1should reduce net – If ij = 1, ij * class(ij) < 0, need to reduce w (ij *w is reduced ) – If ij = -1, ij * class(ij) >0 need to increase w (ij *w is reduced )
ADALINE
ADALINE
Adaline Learning Algorithm
Adaline Learning
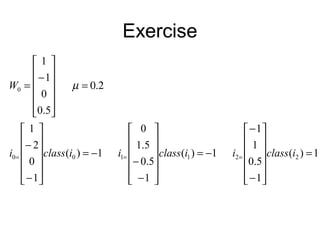
Exercise 1)( 1 5.0 1 1 1)( 1 5.0 5.1 0 1)( 1 0 2 1 5.0 0 1 1 221100 0 =             − − −=             − − −=             − − 0.2=             − = === iclassiiclassiiclassi W µ
[ ] [ ]             − − =             − − −+             − = = =             − −= =             − =             − − −+             − = −∗+== =−++=             − − −= = 2.0 0 4.0 1.0 1 0 2 1 *2*2.0 2.0 0 4.0 3.0 1 1 1 5.0 5.1 0 2.004.03.0 * 2.0 0 4.0 3.0 1 0 2 1 *5.3*2.0 5.0 0 1 1 *)(1 5.25.0021 1 0 2 1 5.0011 * 2 1 1 111 1 00010 0 000 W o net iWnet W inetdWWo net iWnet T T µ
[ ] [ ] 6.0 1 0 2 1 1.015.01.04.0 1.0 15.0 1.0 4.0 1 5.0 1 1 *5.1*2.0 2.0 0 4.0 1.0 1)(1 5.0 1 5.0 1 1 2.004.01.0 * 3 3 22 2 222 −=             − − −−−=             − − − =             − − +             − − = =≠−= −=             − − −−= = net onVerificati W iclasso net iWnet T
Multi-layer networks
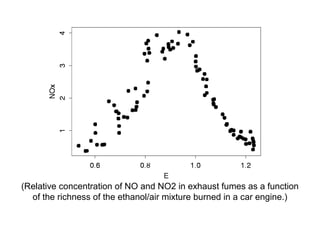
(Relative concentration of NO and NO2 in exhaust fumes as a function of the richness of the ethanol/air mixture burned in a car engine.)
feedforward network
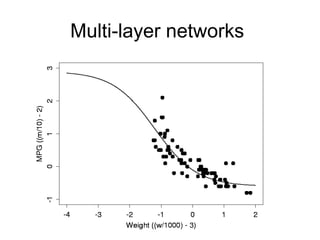
Error Backpropagation We want to train a multi-layer feedforward network by gradient descent to approximate an unknown function, based on some training data consisting of pairs (x,t). The vector x represents a pattern of input to the network, and the vector t the corresponding target (desired output). Weight from unit j to unit i by wij.
Algorithm
Artificial neural netwoks2
Artificial neural netwoks2
Artificial neural netwoks2
Artificial neural netwoks2
Artificial neural netwoks2

More Related Content

Artificial neural netwoks2