Auto-Encoders and Variational Auto-Encoders
- 2. In this chapter, we will discuss about β’ What is Autoencoder - neural networks whose dimension of input and output are same - if the autoencoder use only linear activations and the cost function is MES, then it is same to PCA - the architecture of a stacked autoencoder is typically symmetrical
- 3. Contents β’ Autoencoders β’ Denoising Autoencoders β’ Variational Autoencoders
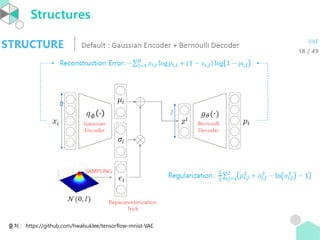
- 5. Introduction β’ Autoencoder λ encoder μ decoder λ‘ λλλ€. μ€λ₯Έμͺ½ diagram μμ π κ° encoder μ΄κ³ , π κ° decoder μ΄λ€. β’ cost function μ reconstruction error λ₯Ό μ¬μ©νλ€: πΏ(π₯, π π π₯ = π₯ β π π π₯ 2 β’ hidden layer κ° 2κ° μ΄μμΈ AEλ₯Ό stacked Autoencoder λΌκ³ νλ€. β’ e.g. linear activation λ§ μ¬μ©νκ³ , cost function μΌλ‘ MSE λ₯Ό μ¬μ© ν Autoencoder λ PCA μ΄λ€. π₯ β π π π
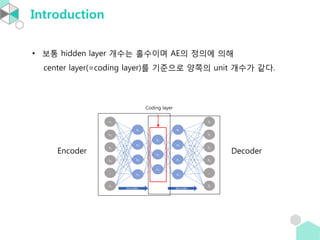
- 6. Introduction β’ λ³΄ν΅ hidden layer κ°μλ νμμ΄λ©° AEμ μ μμ μν΄ center layer(=coding layer)λ₯Ό κΈ°μ€μΌλ‘ μμͺ½μ unit κ°μκ° κ°λ€. Coding layer Encoder Decoder
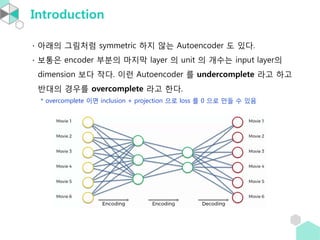
- 7. Introduction β μλμ κ·Έλ¦Όμ²λΌ symmetric νμ§ μλ Autoencoder λ μλ€. β 보ν΅μ encoder λΆλΆμ λ§μ§λ§ layer μ unit μ κ°μλ input layerμ dimension λ³΄λ€ μλ€. μ΄λ° Autoencoder λ₯Ό undercomplete λΌκ³ νκ³ λ°λμ κ²½μ°λ₯Ό overcomplete λΌκ³ νλ€. * overcomplete μ΄λ©΄ inclusion + projection μΌλ‘ loss λ₯Ό 0 μΌλ‘ λ§λ€ μ μμ
- 8. Cost function β’ [VLBM, p.2] An autoencoder takes an input vector π₯ β 0,1 π , and first maps it to a hidden representation y β 0,1 πβ² through a deterministic mapping π¦ = ππ π₯ = π (ππ₯ + π), parameterized by π = {π, π}. π is a π Γ πβ² weight matrix and π is a bias vector. The resulting latent representation π¦ is then mapped back to a βreconstructedβ vector z β 0,1 π in input space π§ = π πβ² π¦ = π πβ² π¦ + πβ² with πβ² = {πβ², πβ²}. The weight matrix πβ² of the reverse mapping may optionally be constrained by πβ² = π π, in which case the autoencoder is said to have tied weights. β’ The parameters of this model are optimized to minimize the average reconstruction error: πβ , πβ²β = arg min π,πβ² 1 π π=1 π πΏ(π₯ π , π§ π ) = arg min π,πβ² 1 π π=1 π πΏ(π₯ π , π πβ²(ππ π₯ π ) (1) where πΏ π₯ β π§ = π₯ β π§ 2.
- 9. Cost function β’ [VLBM,p.2] An alternative loss, suggested by the interpretation of π₯ and π§ as either bit vectors or vectors of bit probabilities (Bernoullis) is the reconstruction cross-entropy: πΏ π» π₯, π§ = π»(π΅π₯||π΅π§) = β π=1 π [π₯ π log π§ π + log 1 β π₯ π log(1 β π§ π)] where π΅π π₯ = (π΅π1 π₯ , β― , π΅π π π₯ ) is a Bernoulli distribution. β’ [VLBM,p.2] Equation (1) with πΏ = πΏ π» can be written πβ, πβ²β = arg min π,πβ² πΈ π0 [πΏ π»(π, π πβ²(ππ π ))] where π0(π) denotes the empirical distribution associated to our π training inputs.
- 11. Denoising Autoencoders β’ [VLBM,p.3] corrupted input λ₯Ό λ£μ΄ repaired input μ μ°Ύλ training μ νλ€. μ’ λ μ ννκ² λ§νλ©΄ input dataμ dimension μ΄ π λΌκ³ ν λ βdesired proportion π of destructionβ μ μ νμ¬ ππ λ§νΌμ input μ 0 μΌλ‘ μμ νλ λ°©μμΌλ‘ destruction νλ€. μ¬κΈ°μ ππ κ° components λ random μΌλ‘ μ νλ€. μ΄ν reconstruction error λ₯Ό 체ν¬νμ¬ destruction μ μ input μΌλ‘ 볡ꡬνλ cost function μ΄μ©νμ¬ νμ΅μ νλ Autoencoder κ° Denoising Autoencoder μ΄λ€. μ¬κΈ°μ π₯ μμ destroyed version μΈ π₯ λ₯Ό μ»λ κ³Όμ μ stochastic mapping π₯ ~ π π·( π₯|x) λ₯Ό λ°λ₯Έλ€.
- 12. Denoising Autoencoders β’ [VLBM,p.3] Let us define the joint distribution π0 π, π, π = π0 π π π· π π πΏπ π π (π)) where πΏ π’(π£) is the Kronecker delta. Thus π is a deterministic function of π. π0(π, π, π) is parameterized by π. The objective function minimized by stochastic gradient descent becomes: πππ πππ π,πβ² πΈ π0 π₯, π₯ [πΏ π»(π₯, π πβ²(ππ( π₯))]) Corrupted π₯ λ₯Ό μ λ ₯νκ³ π₯ λ₯Ό μ°Ύλ λ°©λ²μΌλ‘ νμ΅!
- 13. Other Autoencoders β’ [DL book, 14.2.1] A sparse autoencoder is simply an autoencoder whose training criterion involves a sparsity penalty Ξ© β on the code layer h, in addition to the reconstruction error: πΏ(π₯, π π π₯ ) + Ξ©(β), where π β is the decoder output and typically we have β = π(π₯), the encoder output. β’ [DL book, 14.2.3] Another strategy for regularizing an autoencoder is to use a penalty Ξ© as in sparse autoencoders, πΏ π₯, π π π₯ ) + Ξ©(β, π₯ , but with a different form of Ξ©: Ξ© β, π₯ = π π π»π₯βπ 2
- 15. Reference β’ Reference. Auto-Encoding Variational Bayes, Diederik P Kingma, Max Welling, 2013 β’ [λ Όλ¬Έμ κ°μ ] We will restrict ourselves here to the common case where we have an i.i.d. dataset with latent variables per datapoint, and where we like to perform maximum likelihood (ML) or maximum a posteriori (MAP) inference on the (global) parameters, and variational inference on the latent variables.
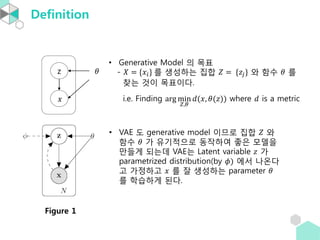
- 16. Definition β’ Generative Model μ λͺ©ν - π = {π₯π} λ₯Ό μμ±νλ μ§ν© π = {π§π} μ ν¨μ π λ₯Ό μ°Ύλ κ²μ΄ λͺ©νμ΄λ€. i.e. Finding arg min π,π π(π₯, π(π§)) where π is a metric β’ VAE λ generative model μ΄λ―λ‘ μ§ν© π μ ν¨μ π κ° μ κΈ°μ μΌλ‘ λμνμ¬ μ’μ λͺ¨λΈμ λ§λ€κ² λλλ° VAEλ Latent variable π§ κ° parametrized distribution(by π) μμ λμ¨λ€ κ³ κ°μ νκ³ π₯ λ₯Ό μ μμ±νλ parameter π λ₯Ό νμ΅νκ² λλ€. Figure 1 z π₯ π
- 17. Problem scenario β’ Dataset π = π₯ π π=1 π λ i.i.d μΈ continuous(λλ discrete) variable π₯ μ sample μ΄λ€. π λ unobserved continuous variable π§ μ some random process λ‘ μμ±λμλ€κ³ κ°μ νμ. μ¬κΈ°μ random process λ λ κ°μ step μΌλ‘ ꡬμ±λμ΄μλ€: (1) π§(π) is generated from some prior distribution π πβ(π§) (2) π₯(π) is generated from some conditional distribution π πβ(π₯|π§) β’ Prior π πβ π§ μ likelihood π πβ(π₯|π§) λ differentiable almost everywhere w.r.t π and π§ μΈ parametric families of distributions π π(π§)μ π π(π₯|π§) λ€μ μμ μ¨ κ²μΌλ‘ κ°μ νμ. β’ μμ½κ²λ true parameter πβ μ latent variables π§(π) μ κ°μ μ μ μμ΄μ cost function μ μ νκ³ κ·Έκ²μ lower bound λ₯Ό ꡬνλ λ°©ν₯μΌλ‘ μ κ°λ μμ μ΄λ€.
- 18. Intractibility and Variational Inference β’ π π π₯ = π π π₯ π π π₯ π§ ππ§ is intractable(κ³μ° λΆκ°λ₯) β΅ π π π§ π₯ = π π π₯ π§ π π(π§)/π π(π₯) is intractable β’ π π π§ π₯ λ₯Ό μ μ μμΌλ μ°λ¦¬κ° μλ ν¨μλΌκ³ κ°μ νμ. μ΄λ° λ°©λ²μ variational inference λΌκ³ νλ€. μ¦, μ μλ ν¨μ π π(π§|π₯) λ₯Ό π π π§ π₯ λμ μ¬μ©νλ λ°©λ²μ variational inference λΌκ³ νλ€. β’ Idea : prior π π π§ π₯ λ₯Ό π π(π§|π₯) λ‘ μ¬μ©ν΄λ λλ μ΄μ λ μ£Όμ΄μ§ input π§ κ° π₯ μ κ·Όμ¬νκ² νμ΅μ΄ λλ€.
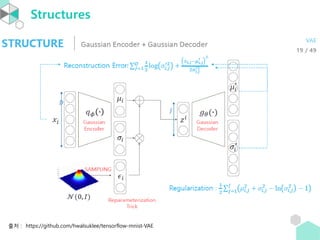
- 19. Then variational bound β’ μ°λ¦¬λ π = π₯ π π=1 π κ° i.i.d λ₯Ό λ§μ‘±νλ€κ³ κ°μ νμΌλ―λ‘ log π π(π₯ 1 , β― , π₯(π) ) = π=1 π log π π(π₯ π ) μ΄λ€. β’ κ°κ°μ π₯ β πμ λν΄ μλ μμ μ»μ μ μλ€: log π π π₯ = π§ π π π§ π₯ log π π(π₯) ππ§ = π§ π π π§ π₯ log π π π§,π₯ π π(π§|π₯) ππ§ = π§ π π π§ π₯ log π π π§,π₯ π π π§ π₯ π π π§ π₯ π π π§ π₯ ππ§ = π§ π π π§ π₯ log π π π§,π₯ π π π§ π₯ ππ§ + π§ π π π§ π₯ π π π§ π₯ π π π§ π₯ ππ§ = π π, π; π₯ + π· πΎπΏ(π π(π§|π₯)||π π π§ π₯ ) (1) β₯ π π, π; π₯ μΈμ λ πΎπΏ divergence λ 0 μ΄μμ΄λ―λ‘ π§ π π π§ π₯ log π π π§,π₯ π π π§ π₯ ππ§ λ lower bound κ° λλ€. μ΄κ² μ π π, π; π₯ λΌκ³ λμ.
- 20. Cost function β’ (Eq.3) π π, π; π₯ = βπ· πΎπΏ(π π(π§|π₯)||π π π₯ ) + πΈ π π π§ π₯ [log π π(π₯|π§)] <Proof> π π, π; π₯ = π§ π π π§ π₯ log π π(π§,π₯) π π(π§|π₯) ππ§ = π§ π π π§ π₯ log π π π§)π π(π₯|π§ π π (π§|π₯) ππ§ = π§ π π π§ π₯ log π π(π§) π π (π§|π₯) ππ§ + π§ π π π§ π₯ log π π π₯ π§ ππ§ = βπ· πΎπΏ(π π(π§|π₯)| π π(π§) + πΈ π π π§ π₯ [log π π(π₯|π§)] π πμ π πκ° normal μ΄λ©΄ κ³μ° κ°λ₯! Reconstruction error
- 21. Cost function β’ Lemma. If π π₯ ~π π1, π1 2 and π π₯ ~π π2, π2 2 , then πΎπΏ(π(π₯)||π π₯ ) = ln π2 π1 + π1 2 + π1 β π2 2 2π2 2 β 1 2 β’ Corollary. π π π§ π₯ ~ π(ππ, ππ 2 πΌ) μ΄κ³ π π§ ~π 0,1 μ΄λ©΄ πΎπΏ π π π§ π₯π π π§ = 1 2 (π‘π ππ 2 πΌ + ππ π ππ β π½ + ln 1 π=π π½ ππ,π 2 ) = (Ξ£π=1 π½ ππ,π 2 + Ξ£π=1 π½ ππ,π 2 β π½ β Ξ£π=1 π½ ln(ππ,π 2 )) = 1 2 Ξ£π=1 π½ (ππ,π 2 + ππ,π 2 β 1 β ln ππ,π 2 ) β’ μ¦, π π π§ π₯ ~ π(ππ, ππ 2 πΌ) μ΄κ³ π π§ ~π 0,1 μ΄λ©΄ Eq.3 λ μλμ κ°λ€. π π, π; π₯ = 1 2 Ξ£π=1 π½ ππ,π 2 + ππ,π 2 β 1 β ln ππ,π 2 + πΈ π π π§ π₯ [log π π(π₯|π§)]
- 22. Reconstruction error νμ΅ λ°©λ² β’ πΈ π π π§ π₯ [log π π(π₯|π§)]λ sampling μ ν΅ν΄ Monte-carlo estimation νλ€. μ¦, π₯π β X λ§λ€ π§ π,1 , β― , π§ π πΏ λ₯Ό sampling νμ¬ log likelihood μ meanμΌλ‘ κ·Όμ¬μν¨λ€. λ³΄ν΅ πΏ = 1 μ λ§μ΄ μ¬μ©νλ€. πΈ π π π§ π₯ [log π π(π₯|π§)] βΌ 1 πΏ Ξ£π=1 πΏ log(π π π₯π π§ π,π ) β’ μ΄λ κ² sampling μ νλ©΄ backpropagation μ ν μ μλ€. κ·Έλμ μ¬μ© λλ λ°©λ²μ΄ reparametrization trick μ΄λ€. π π π₯ π§ π π π₯ π§
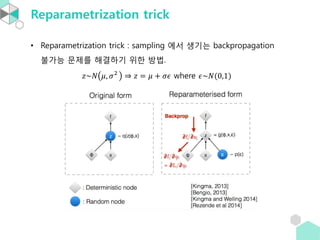
- 23. Reparametrization trick β’ Reparametrization trick : sampling μμ μκΈ°λ backpropagation λΆκ°λ₯ λ¬Έμ λ₯Ό ν΄κ²°νκΈ° μν λ°©λ². π§~π π, π2 β π§ = π + ππ where π~π(0,1)
- 24. Log Likelihood β’ μμμ reconstruction error λ₯Ό κ³μ°ν λ νλμ© sampling μ νλ©΄ πΈ π π π§ π₯ [log π π(π₯|π§)] βΌ 1 πΏ Ξ£π=1 πΏ log π π π₯π π§ π,π = log(π π(π₯π|π§ π ) κ° λλ€. μ¬κΈ°μ π π π₯π π§ π μ λΆν¬κ° Bernoulli μΈ κ²½μ°μ μλμ μμ μ»μ μ μλ€. μΆμ² : https://github.com/hwalsuklee/tensorflow-mnist-VAE
- 25. Log Likelihood β’ π π π₯π π§ π μ λΆν¬κ° normal μΈ κ²½μ°μ μλμ μμ μ»μ μ μλ€. μΆμ² : https://github.com/hwalsuklee/tensorflow-mnist-VAE
- 28. Examples of VAE μΆμ² : https://github.com/hwalsuklee/tensorflow-mnist-VAE
- 29. Examples of DAE μΆμ² : https://github.com/hwalsuklee/tensorflow-mnist-VAE
- 30. References β’ [VLBM] Extracting and composing robust features with denoising autoencoders, Vincent, Larochelle, Bengio, Manzagol, 2008 β’ [KW] Auto-Encoding Variational Bayes, Diederik P Kingma, Max Welling, 2013 β’ [D] Tutorial on Variational Autoencoders - Carl Doersch, 2016 β’ PR-010: Auto-Encoding Variational Bayes, ICLR 2014, μ°¨μ€λ² β’ μ€ν μΈμ½λμ λͺ¨λ κ², μ΄νμ https://github.com/hwalsuklee/tensorflow-mnist-VAE




![Cost function
β’ [VLBM, p.2] An autoencoder takes an input vector π₯ β 0,1 π
, and first
maps it to a hidden representation y β 0,1 πβ²
through a deterministic
mapping π¦ = ππ π₯ = π (ππ₯ + π), parameterized by π = {π, π}.
π is a π Γ πβ²
weight matrix and π is a bias vector. The resulting latent
representation π¦ is then mapped back to a βreconstructedβ vector
z β 0,1 π in input space π§ = π πβ² π¦ = π πβ² π¦ + πβ² with πβ² = {πβ², πβ²}.
The weight matrix πβ² of the reverse mapping may optionally be
constrained by πβ² = π π, in which case the autoencoder is said to
have tied weights.
β’ The parameters of this model are optimized to minimize
the average reconstruction error:
πβ
, πβ²β
= arg min
π,πβ²
1
π
π=1
π
πΏ(π₯ π
, π§ π
)
= arg min
π,πβ²
1
π π=1
π
πΏ(π₯ π
, π πβ²(ππ π₯ π
) (1)
where πΏ π₯ β π§ = π₯ β π§ 2.](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-8-320.jpg)
![Cost function
β’ [VLBM,p.2] An alternative loss, suggested by the interpretation of π₯
and π§ as either bit vectors or vectors of bit probabilities (Bernoullis) is
the reconstruction cross-entropy:
πΏ π» π₯, π§ = π»(π΅π₯||π΅π§)
= β π=1
π
[π₯ π log π§ π + log 1 β π₯ π log(1 β π§ π)]
where π΅π π₯ = (π΅π1
π₯ , β― , π΅π π
π₯ ) is a Bernoulli distribution.
β’ [VLBM,p.2] Equation (1) with πΏ = πΏ π» can be written
πβ, πβ²β = arg min
π,πβ²
πΈ π0 [πΏ π»(π, π πβ²(ππ π ))]
where π0(π) denotes the empirical distribution associated to our π
training inputs.](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-9-320.jpg)

![Denoising Autoencoders
β’ [VLBM,p.3] corrupted input λ₯Ό λ£μ΄ repaired input μ μ°Ύλ training
μ νλ€. μ’ λ μ ννκ² λ§νλ©΄ input dataμ dimension μ΄ π λΌκ³
ν λ βdesired proportion π of destructionβ μ μ νμ¬ ππ λ§νΌμ
input μ 0 μΌλ‘ μμ νλ λ°©μμΌλ‘ destruction νλ€. μ¬κΈ°μ ππ κ°
components λ random μΌλ‘ μ νλ€. μ΄ν reconstruction error λ₯Ό
체ν¬νμ¬ destruction μ μ input μΌλ‘ 볡ꡬνλ cost function
μ΄μ©νμ¬ νμ΅μ νλ Autoencoder κ° Denoising Autoencoder μ΄λ€.
μ¬κΈ°μ π₯ μμ destroyed version μΈ π₯ λ₯Ό μ»λ κ³Όμ μ stochastic
mapping π₯ ~ π π·( π₯|x) λ₯Ό λ°λ₯Έλ€.](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-11-320.jpg)
![Denoising Autoencoders
β’ [VLBM,p.3] Let us define the joint distribution
π0
π, π, π = π0
π π π· π π πΏπ π π
(π))
where πΏ π’(π£) is the Kronecker delta. Thus π is a deterministic
function of π. π0(π, π, π) is parameterized by π. The objective
function minimized by stochastic gradient descent becomes:
πππ πππ
π,πβ²
πΈ π0 π₯, π₯ [πΏ π»(π₯, π πβ²(ππ( π₯))])
Corrupted π₯ λ₯Ό μ
λ ₯νκ³ π₯ λ₯Ό μ°Ύλ λ°©λ²μΌλ‘ νμ΅!](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-12-320.jpg)
![Other Autoencoders
β’ [DL book, 14.2.1] A sparse autoencoder is simply an autoencoder
whose training criterion involves a sparsity penalty Ξ© β on the
code layer h, in addition to the reconstruction error:
πΏ(π₯, π π π₯ ) + Ξ©(β),
where π β is the decoder output and typically we have β = π(π₯),
the encoder output.
β’ [DL book, 14.2.3] Another strategy for regularizing an autoencoder
is to use a penalty Ξ© as in sparse autoencoders,
πΏ π₯, π π π₯ ) + Ξ©(β, π₯ ,
but with a different form of Ξ©:
Ξ© β, π₯ = π
π
π»π₯βπ
2](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-13-320.jpg)

![Reference
β’ Reference. Auto-Encoding Variational Bayes, Diederik P Kingma,
Max Welling, 2013
β’ [λ
Όλ¬Έμ κ°μ ] We will restrict ourselves here to the common case
where we have an i.i.d. dataset with latent variables per datapoint,
and where we like to perform maximum likelihood (ML) or
maximum a posteriori (MAP) inference on the (global) parameters,
and variational inference on the latent variables.](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-15-320.jpg)



![Cost function
β’ (Eq.3) π π, π; π₯ = βπ· πΎπΏ(π π(π§|π₯)||π π π₯ ) + πΈ π π π§ π₯ [log π π(π₯|π§)]
<Proof>
π π, π; π₯ = π§
π π π§ π₯ log
π π(π§,π₯)
π π(π§|π₯)
ππ§
= π§
π π π§ π₯ log
π π π§)π π(π₯|π§
π π (π§|π₯)
ππ§
= π§
π π π§ π₯ log
π π(π§)
π π (π§|π₯)
ππ§ + π§
π π π§ π₯ log π π π₯ π§ ππ§
= βπ· πΎπΏ(π π(π§|π₯)| π π(π§) + πΈ π π π§ π₯ [log π π(π₯|π§)]
π πμ π πκ° normal μ΄λ©΄ κ³μ° κ°λ₯!
Reconstruction error](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-20-320.jpg)
![Cost function
β’ Lemma. If π π₯ ~π π1, π1
2
and π π₯ ~π π2, π2
2
, then
πΎπΏ(π(π₯)||π π₯ ) = ln
π2
π1
+
π1
2
+ π1 β π2
2
2π2
2 β
1
2
β’ Corollary. π π π§ π₯ ~ π(ππ, ππ
2
πΌ) μ΄κ³ π π§ ~π 0,1 μ΄λ©΄
πΎπΏ π π π§ π₯π π π§ =
1
2
(π‘π ππ
2
πΌ + ππ π
ππ β π½ + ln
1
π=π
π½
ππ,π
2
)
= (Ξ£π=1
π½
ππ,π
2
+ Ξ£π=1
π½
ππ,π
2
β π½ β Ξ£π=1
π½
ln(ππ,π
2
))
=
1
2
Ξ£π=1
π½
(ππ,π
2
+ ππ,π
2
β 1 β ln ππ,π
2
)
β’ μ¦, π π π§ π₯ ~ π(ππ, ππ
2
πΌ) μ΄κ³ π π§ ~π 0,1 μ΄λ©΄ Eq.3 λ μλμ κ°λ€.
π π, π; π₯ =
1
2
Ξ£π=1
π½
ππ,π
2
+ ππ,π
2
β 1 β ln ππ,π
2
+ πΈ π π π§ π₯ [log π π(π₯|π§)]](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-21-320.jpg)
![Reconstruction error νμ΅ λ°©λ²
β’ πΈ π π π§ π₯ [log π π(π₯|π§)]λ sampling μ ν΅ν΄ Monte-carlo estimation νλ€.
μ¦, π₯π β X λ§λ€ π§ π,1
, β― , π§ π πΏ λ₯Ό sampling νμ¬ log likelihood μ meanμΌλ‘
κ·Όμ¬μν¨λ€. λ³΄ν΅ πΏ = 1 μ λ§μ΄ μ¬μ©νλ€.
πΈ π π π§ π₯ [log π π(π₯|π§)] βΌ
1
πΏ
Ξ£π=1
πΏ
log(π π π₯π π§ π,π )
β’ μ΄λ κ² sampling μ νλ©΄ backpropagation μ ν μ μλ€. κ·Έλμ μ¬μ©
λλ λ°©λ²μ΄ reparametrization trick μ΄λ€.
π π π₯ π§ π π π₯ π§](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-22-320.jpg)
![Log Likelihood
β’ μμμ reconstruction error λ₯Ό κ³μ°ν λ νλμ© sampling μ νλ©΄
πΈ π π π§ π₯ [log π π(π₯|π§)] βΌ
1
πΏ
Ξ£π=1
πΏ
log π π π₯π π§ π,π
= log(π π(π₯π|π§ π
)
κ° λλ€. μ¬κΈ°μ π π π₯π π§ π
μ λΆν¬κ° Bernoulli μΈ κ²½μ°μ μλμ μμ
μ»μ μ μλ€.
μΆμ² : https://github.com/hwalsuklee/tensorflow-mnist-VAE](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-24-320.jpg)



![References
β’ [VLBM] Extracting and composing robust features with denoising
autoencoders, Vincent, Larochelle, Bengio, Manzagol, 2008
β’ [KW] Auto-Encoding Variational Bayes, Diederik P Kingma, Max
Welling, 2013
β’ [D] Tutorial on Variational Autoencoders - Carl Doersch, 2016
β’ PR-010: Auto-Encoding Variational Bayes, ICLR 2014, μ°¨μ€λ²
β’ μ€ν μΈμ½λμ λͺ¨λ κ², μ΄νμ
https://github.com/hwalsuklee/tensorflow-mnist-VAE](https://image.slidesharecdn.com/auto-encoders-180909040543/85/Auto-Encoders-and-Variational-Auto-Encoders-30-320.jpg)