�ݺ�ߣ

AVL TREE & Hash Table
Waseem Usman (BSCS-S16-LC-023)
Irfan Khan (BSCS-S16-LC-007)
Asad Tahir (BSCS-S16-LC-019)
Zafeer Ramzan (BSCS-S16-LC-002)

AVL TREE
A binary search tree x is called an AVL tree, if:
• b(x.key) ∈ {−1, 0, 1}, and
• x.leftChild and x.rightChild are both AVL trees = the height balance of every node
must be -1, 0, or 1
A
B C
D E
0 0
0 0
1
• Named after their inventor Adelson, Velski & Landis, AVL trees are height
balancing binary search tree.

Balance Factor.
AVL tree checks the height of the left and the right sub-trees and assures that the
difference is not more than 1 or less then -1. This difference is called the Balance
Factor.
BalanceFactor = height(left-subtree) − height(right-subtree)

AVL ROTATIONS
To balance itself, an AVL tree may perform the following four kinds of rotations −
• Left rotation
• Right rotation
• Left-Right rotation
• Right-Left rotation
The first two rotations are single rotations and the next two rotations are double
rotations. To have an unbalanced tree, we at least need a tree of height 2. With this
simple tree, let's understand them one by one.

LEFT & RIGHT ROTATION
• If a tree becomes unbalanced, when a
node is inserted into the right subtree of
the right subtree, then we perform a single
left rotation −
• AVL tree may become unbalanced, if a
node is inserted in the left subtree of the
left subtree. The tree then needs a right
rotation.

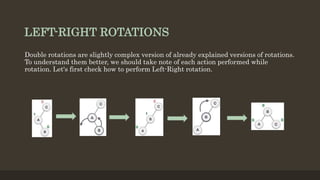
LEFT-RIGHT ROTATIONS
Double rotations are slightly complex version of already explained versions of rotations.
To understand them better, we should take note of each action performed while
rotation. Let's first check how to perform Left-Right rotation.

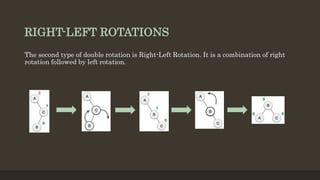
RIGHT-LEFT ROTATIONS
The second type of double rotation is Right-Left Rotation. It is a combination of right
rotation followed by left rotation.

HASH TABLE
Asad Tahir
Zafeer Ramzan

HASHING
• Searching technique based on hash table.
• It is the application of a function to the key value that results in mapping the range of
possible key values into smaller range of relative address.
• If two different Keys have assign same address then Collision occurs.
Data
{ Key H(K)
Hash Function
Address
K1
K2
H(K) Address{Collision

TYPES OF HASHING FUNCTIONS
• Direct Hashing.
• Modulo - Division Hashing.
• Mid - Square Hashing.
• Folding Hashing.
• Pseudo Random Hashing.
• Subtraction Hashing.

DIRECT HASHING
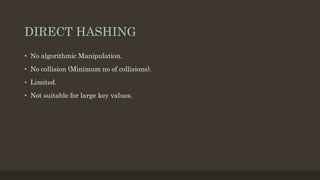
• No algorithmic Manipulation.
• No collision (Minimum no of collisions).
• Limited.
• Not suitable for large key values.

MODULO - DIVISION HASHING
• Also known as Division - Remainder.
• Works with any list size.
• If list size is a prime no than fewer collisions.
• In Which “ K ” is a Key and “ n ” is a List size.
H(K) = K mod n

MID - SQUARE HASHING
• Middle of square.
• Key is squared and the address is selected from the middle of the square no.
Problem :-
Non-Uniform distribution of the key.

FOLDING HASHING
1- FOLD – SHIFT HASHING
Key value is divided into two parts whose size matches the size of the required
address.
2- FOLD – BOUNDARY HASHING
Left and Right no are folded on a fixed boundary between them and the
center no.

PSEUDO RANDOM HASHING
• In which “ a ” is a Chosen Coefficient “ c ” is a Constant and “ n ” is a List size.
Y = ax + c
X = key
H(K) = Y mod n

SUBTRACTION HASHING
• Subtract a fixed no from key.
• In which “ c ” is a fixed no.
• Like Direct Hashing.
• No Collision.
• Suitable for small lists.
H(K) = K-c

�ݺ�ߣ

Avl tree-hash-table

More Related Content

Avl tree-hash-table