础痴齿命令を用いた尝闯の力计算の厂滨惭顿化
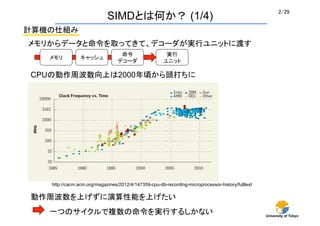
- 2. University of Tokyo 2/29 SIMDとは何か? (1/4) 一つのサイクルで複数の命令を実行するしかない 計算機の仕組み 命令 デコーダ 実行 ユニット キャッシュ メモリ メモリからデータと命令を取ってきて、デコーダが実行ユニットに渡す 動作周波数を上げずに演算性能を上げたい CPUの動作周波数向上は2000年頃から頭打ちに http://cacm.acm.org/magazines/2012/4/147359-cpu-db-recording-microprocessor-history/fulltext
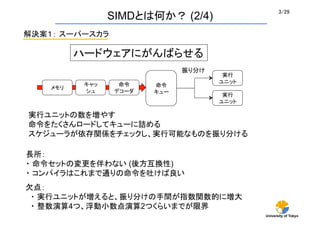
- 3. University of Tokyo 3/29 解決案1: スーパースカラ 命令 デコーダ 実行 ユニット キャッ シュ メモリ 実行 ユニット 欠点: ? 実行ユニットが増えると、振り分けの手間が指数関数的に増大 ? 整数演算4つ、浮動小数点演算2つくらいまでが限界 SIMDとは何か? (2/4) 実行ユニットの数を増やす 命令をたくさんロードしてキューに詰める スケジューラが依存関係をチェックし、実行可能なものを振り分ける 長所: ? 命令セットの変更を伴わない (後方互換性) ? コンパイラはこれまで通りの命令を吐けば良い ハードウェアにがんばらせる 命令 キュー 振り分け
- 4. University of Tokyo 4/29 解決案2: VLIW 命令 デコーダ 実行 ユニット キャッ シュ メモリ 実行 ユニット コンパイラにがんばらせる 命令A 命令B 実行ユニットの数は複数用意しておく コンパイラが予め並列実行可能な命令を並べておき、そのまま実行ユニットに流す 長所: ? 依存関係チェックが不要になるため、ハードウェアは簡単になる ? コード全体を調べるため、より積極的な最適化が可能 短所: ? コンパイラ作るのが死ぬほど大変 ? 後方互換性を失う (命令セットが変わるため) SIMDとは何か? (3/4)
- 5. University of Tokyo 5/29 SIMDとは何か? (4/4) 命令 デコー ダ 実行 ユニット キャッ シュ メモリ 解決案3: SIMD プログラマにがんばらせる 実行ユニットの数は増やさない 複数のデータに、同じ演算を一度に行う 長所: ? ハードウェアが簡単になる ? SIMDは命令セットの拡張という形で入るため、後方互換性もそれなり 短所: ? コンパイラがSIMD命令を効率的に吐くのは難しい ? プログラマが明示的にSIMD命令を使う必要がある 現在はスーパースカラ+SIMDが主流 実行ユニットの数は増えず、SIMD幅が増えていく傾向
- 6. University of Tokyo 6/29 http://news.mynavi.jp/photo/articles/2016/09/08/hc28_arm2/images/009l.jpg ポスト京 ソフトウェア: ? SVE (Scalable Vector Extension) ? 512?2048bitの可変長ベクトル命令 ハードウェア: ?512bit (倍精度64bit × 8個)で実装 なんでSIMD化するの? A: SIMD化しないと性能が出なくなっていくから システムB Haswell、AVX命令 ?256bit (倍精度64bit × 4個) (2016年8月公表@Hot Chips 28) 京 SPARC-VIIIxfx, HPC-ACE ?128bit (倍精度64bit × 2個) 128bitくらいまでならスルーできたが、512bitだと真面目にやらないと苦しい?
- 9. University of Tokyo 9/29 ペアリストとBookkeeping法 (1/2) 相互作用ペアリスト カットオフ距離以内にある相互作用原子ペアを探す 全探索するとO(N^2)となるので、空間をセルに区切ってO(N)に落とす 空間をセルに切る 原子をセルに登録する セル内、隣接セルで相互作用ペアを探索する セルの大きさは、相互作用が次近接のセルに届かないようにとる
- 10. University of Tokyo 10/29 Bookkeepingによるペアリスト再利用 ペアリストとBookkeeping法 (2/2) 相互作用ペア探索は重い処理 → 探索距離を長めにとって何ステップか再利用する 原子がマージンを横切るまでこのペアリストは再利用できる 相互作用距離 探索距離 マージン ? マージンを「ペアリストの寿命」とする ? 系の最速の原子を探し、その速度をvとする ? マージンから v*2*dtだけ引く (dtは時間刻み) ? まだマージンが残っていればペアリストを再利用 ? マージンが無くなったらペアリスト再構築 相互作用距離 マージン 最悪のケース 最速と次最速の原子が、お互いに近づく時 → 系の最速の原子がマージンの半分を 横切るまではペアリストが有効 有効期限判定
- 11. University of Tokyo 11/29 相互作用ペアソート (1/2) 力の計算とペアリスト 力の計算はペアごとに行う 相互作用範囲内にあるペアは配列に格納 ペアの番号の若い方をi粒子、相手をj粒子と呼ぶ 得られた相互作用ペア 相互作用ペアの配列表現 1 0 0 2 3 3 1 1 2 3 0 2 9 2 1 7 9 5 2 4 8 4 5 6 このまま計算すると 2個の粒子の座標を取得 (48Byte) 運動量の読み書き (96Byte) 力の計算が50演算程度とすると、B/F?3.0を要求 1 9 0 2 0 1 2 7 3 9 3 5 1 2 1 4 2 8 3 4 0 5 2 6 i粒子 j粒子 i粒子 j粒子
- 12. University of Tokyo 12/29 相互作用相手でソート 相互作用ペア 相互作用ペアソート (2/2) 1 9 0 2 0 1 2 7 3 9 3 5 1 2 1 4 2 8 3 4 0 5 2 6 i粒子でソート 1 2 5 2 4 9 6 7 8 4 5 9 Sorted List 0 1 2 5 1 2 4 9 2 6 7 8 3 4 5 9 配列表現 0 1 2 3 i粒子の情報がレジスタにのる → 読み込み、書き込みがj粒子のみ → メモリアクセスが半分に キャッシュに乗る領域でも10%前後の高速化 i粒子 j粒子 i粒子 j粒子
- 13. University of Tokyo 13/29 AVX命令によるSIMD化 前提条件: ? 相互作用相手はペアリストにより間接参照、インデックスは不連続 ? Bookkeeping法により、相互作用していないペアも含まれる
- 14. University of Tokyo 14/29 レジスタとメモリ A[2] 全ての計算は原則としてレジスタ上で行う 「C = A + B」を計算する例: (1)? メモリからAとBをレジスタにロード (2)? レジスタでA+Bを計算 (3)? 結果Cをレジスタからメモリにストア A[1] SIMD SIMD: 複数のデータに対して、一度に同じタイプの演算を行う仕組み SIMD用レジスタ:複数の値を同時に保持、演算できるレジスタ C[1] = A[1]+B[1] C[2] = A[2]+B[2] A B C 1 2 メモリ レジスタ 3 1 2 + 3 ロード ストア B[2] B[1] + C[2] C[1] = 二つ以上の演算を一度に行うことができる x86レジスタ (1/3)
- 15. University of Tokyo 15/29 浮動小数点レジスタ 下位 上位 xmm0 ymm0 浮動小数点演算用に256bitのレジスタが16本用意されている そのうち下位128bitをxmmレジスタ、全体をymmレジスタと呼ぶ 倍精度実数は64bitなので、倍精度実数4つ分の値を保持できる 汎用レジスタ 64bitの汎用レジスタがある 下位32bit, 16bit, 8bitを別名で共有 アドレッシングや整数演算に使う 下位 上位 64bit RAX EAX AX AH AL x86レジスタ (2/3)
- 16. University of Tokyo 16/29 xmmレジスタは倍精度実数二つ分保持できるが、下位64bitを普段使いに使う double func(double a, double b){ return a+b; } func(double, double): addsd %xmm1, %xmm0 ret ソース アセンブリ 関数の引数のdoubleは、順番にxmm0,xmm1に値を入れる 返り値がdoubleの時はxmm0に値を入れる (xmmレジスタの下位64bitだけ使う) 浮動小数点演算 整数演算 int func(int a, int b){ return a+b; } func(int, int): addl %esi, %eax ret ※ 実際にはlealが使われる ソース アセンブリ 関数の引数のint(32bit)は、順番にeax, esi, edx, ecx, ...に値を入れる 返り値がintの時はeaxに値を入れる x86レジスタ (3/3)
- 17. University of Tokyo 17/29 Lennard-Jonesの力計算 (1/2) V (r) = 4 r 12 r 6 f(r) = 48 r13 24 r7 r dx dy ポテンシャル 力 力積 Ix = f ? dx r ? dt ? df ? dx df = ? 48 r14 24 r8 ◆ dt ここをまとめる 計算したい量 ~r = (dx, dy, dz)相対座標 r = |~r|相対距離
- 18. University of Tokyo 18/29 Lennard-Jonesの力計算 (2/2) ~qi = (qi x, qi y, qi z) ~qj = (qj x, qj y, qj z) ~dq = ~qj ~qi r2 = ~dq 2 r6 = r2 ? r2 ? r2 r14 = r6 ? r6 ? r2 減算*3 乗算*3 + 加算*2 乗算*2 乗算*2 df = (48 24 ? r6 ) ? dt r14 乗算*2 + 減算*1 + 除算1 乗算*3 + 加算*3 乗算*3 + 加算*3 ~pi = ~pi df ? ~dq ~pj = ~pj + df ? ~dq 加減乗算 * 27 + 除算*1 LJの力計算は軽い
- 19. University of Tokyo 19/29 力計算の単純SIMD化 (1/2) ナイーブな実装 ?qi x qi x 以下、SIMDベクトルレジスタをハットで表現する ?qj x qj xqj+1 xqj+2 xqj+3 x qi+1 xqi+2 xqi+3 x 4つの座標データをymmレジスタにロードする 4つの座標データをymmレジスタにロードする ※ y, zも同様 ※ y, zも同様 ?dx = ?qj x ?qi x ?r2 = ?dx 2 + ?dy 2 + ?dz 2 あとは同様に計算することで、4対の粒子間の力を同時に計算できる
- 20. University of Tokyo 20/29 相互作用粒子のインデックスは連続ではない → 4つのデータをバラバラにロード D C B A D C B A メモリ レジスタ D C B A A メモリ xmm0 D C B A B A メモリ xmm0 vmovsd vmovhpd D C B A C メモリ D C B A D C メモリ vmovsd vmovhpd B A ymm0 xmm1 xmm1 D C D C xmm1 (1) Aをxmm0下位にロード (2) Bをxmm0上位にロード (3) Cをxmm1下位にロード (4) Dをxmm1上位にロード (5) xmm1全体をymm0上位128bitにコピー vinsertf128 実際に起きること 問題点 ※ これをx,y,z座標それぞれでやる ※ データの書き戻しも同様 力計算の単純SIMD化 (2/2) ※ vgatherdpdでなんとかできるかもしれないが???
- 21. University of Tokyo 21/29 やったこと データを粒子数*4成分の二次元配列で宣言 double q[N][4], p[N][4]; z y x z y x メモリ z y x 0 1 2 z y x 3 粒子番号 うれしいこと (x,y,z)の3成分のデータをymmレジスタに一発ロード ただし、1成分(64bit) は無駄になる z y x z y x メモリ z y x 0 1 2 z y x 3 粒子番号 z y x movupd/movapd ymm0 力計算のSIMD化 (1/5)
- 22. University of Tokyo 22/29 力の計算(1ペア) qj xqj yqj z qi xqi yqi z ?qj ?qi ?dq = ?qj ?qi ?dq 2 dx2dy2 dz2 dxdydz ここから r2 = dx2 + dy2 + dz2 を作りたい SIMDのシャッフル命令を使う 力計算のSIMD化 (2/5)
- 23. University of Tokyo 23/29 シャッフル系命令 レジスターメモリ間の転送は極めてコストが高い なので、レジスタの中でデータを並び替えたい → 豊富なシャッフル系命令が用意されている D C B A ベクトルの並び替え (vpermpd) A B D B 同じ要素の重複可 二つのベクトルの要素を混ぜる (blendpd) D2 C2 B2 A2 D1 C1 B1 A1 D1 C2 B2 A1 どちらの要素をコピーするか選択化 力計算のSIMD化 (3/5)
- 24. University of Tokyo 24/29 力の計算(1ペア) cont. dx2dy2 dz2 dx2 dx2 dy2 dz2 dy2 dz2 相対ベクトルの自乗を並び替える 全部足す r2 r2 r2 力の計算(4ペア) これを4つのペアについて行う r2 A r2 B r2 C r2 D r2 Ar2 A r2 Br2 B r2 Cr2 C r2 Dr2 D r2 Ar2 A r2 Cr2 C r2 Br2 B r2 Dr2 D unpacklpd vshufpd r2 Ar2 C r2 Br2 D あとは4ペア同時に力の計算ができる vpermpd 力計算のSIMD化 (4/5)
- 25. University of Tokyo 25/29 力積の書き戻し dfAdfBdfCdfD dfAdfAdfAdfA ~pi = ~pi df ? ~dq dxAdyAdzA (1) Aペアの力だけ取り出す vpermpd dfAdfAdfAdfApi xpi ypi z pi x pi ypi z= - × (2) 運動量をロード (3) 力積ベクトルの計算 pi xpi ypi z pi xpi ypi z メモリ ymmレジスタ (4) 運動量の書き戻し pi xpi ypi z pi xpi ypi z メモリ ymmレジスタ これを4ペアについて行う vfnmadd213pd vmovupd vmovupd 力計算のSIMD化 (5/5)
- 26. University of Tokyo 26/29 マスク処理 Bookkeeping法により、相互作用範囲外のペアもいる→マスク処理 D2 C2 B2 A2 D1 C1 B1 A1 負 正 正 負 src1 src2 mask D2 C1 B1 A2 vblendvpd: マスクの要素の正負により要素を選ぶ ※ 実際にはmaskの最上位bitが0か1かで判定している 相互作用距離とカットオフ距離でマスクを作成し、力をゼロクリア dfAdfBdfCdfD 0 0 0 0 src1 src2 dfBdfC0 0 ペアAとDが相互作用範囲外 カットオフのマスク処理
- 27. University of Tokyo 27/29 1 9 0 2 0 1 2 7 3 9 3 5 1 2 1 4 2 8 3 4 0 5 2 6 0 1 2 5 1 2 4 9 2 6 7 8 3 4 5 9 pair: ペア毎に力計算 sorted: 相互作用相手でソート next: 手で二段ソフトウェア パイプライニング intrin: 手でSIMD化 計算条件: ?密度1.0 ?カットオフ3.0 ?探索範囲3.3 ?12万粒子, 100回の力計算にかかった時間 86% 83% 70% 47% 実行結果 ソースファイル https://github.com/kaityo256/lj_simd
- 28. University of Tokyo 28/29 SIMD化前 (33行) SIMD化後 (98行) ホットスポットのチューニングとしては許容範囲???? 実際のソースコード 行数は3倍に ここを4倍展開
- 29. University of Tokyo 29/29 まとめと感想 ? AVX命令を使ってLennard-Jones系の力計算をSIMD化した ? レジスタとメモリの間のやり取りは高コスト → ロード/ストアを減らすため、データ構造を工夫 → なるべくレジスタで処理をするため、シャッフル命令を活用 ? SIMD化無しの最速コードに比べて速度向上は33% まとめ 感想 ? やろうと思い立ってから、SIMD化が完成するまで1ヶ月ちょっと ? 実働2週間程度? ? 難しくはないが極めて面倒くさい → 実際に早くなるかはやってみないとわからない ? 「京」では128bit SIMD化により10?15%程度の性能向上 ? Intel Xeonでは256bit SIMD化により 30?40%程度の性能向上 ? 512bit SIMDでは二倍程度は差がでるのではないか?












![University of Tokyo
14/29
レジスタとメモリ
A[2]
全ての計算は原則としてレジスタ上で行う
「C = A + B」を計算する例:
(1)? メモリからAとBをレジスタにロード
(2)? レジスタでA+Bを計算
(3)? 結果Cをレジスタからメモリにストア
A[1]
SIMD
SIMD: 複数のデータに対して、一度に同じタイプの演算を行う仕組み
SIMD用レジスタ:複数の値を同時に保持、演算できるレジスタ
C[1] = A[1]+B[1]
C[2] = A[2]+B[2]
A
B
C
1
2
メモリ
レジスタ
3
1
2
+
3
ロード
ストア
B[2]
B[1]
+
C[2]
C[1]
=
二つ以上の演算を一度に行うことができる
x86レジスタ (1/3)](https://image.slidesharecdn.com/ljavx-161031083209/85/AVX-LJ-SIMD-14-320.jpg)






![University of Tokyo
21/29
やったこと
データを粒子数*4成分の二次元配列で宣言
double q[N][4], p[N][4];
z
y
x
z
y
x
メモリ
z
y
x
0
1
2
z
y
x
3
粒子番号
うれしいこと
(x,y,z)の3成分のデータをymmレジスタに一発ロード
ただし、1成分(64bit) は無駄になる
z
y
x
z
y
x
メモリ
z
y
x
0
1
2
z
y
x
3
粒子番号
z
y
x
movupd/movapd
ymm0
力計算のSIMD化 (1/5)](https://image.slidesharecdn.com/ljavx-161031083209/85/AVX-LJ-SIMD-21-320.jpg)







