Bab 8 struktur rekursif
- 2. Perulangan Rekursif dan Perulangan Iteratif ’éŚ Rekursif adalah suatu proses yang bisa memanggil dirinya sendiri . ’éŚ Perulangan rekursif merupakan salah satu metode didalam pemrograman yang mana dalam sebuah fungsi terdapat instruksi yang memanggil fungsi itu sendri, atau lebih sering disebut memanggil dirinya sendiri. ’éŚ Perulangan iteratif merupakan perulangan yang melakukan proses perulangan terhadap sekelompok instruksi. Perulangan dilakukan dalam batasan syarat tertentu. Ketika syarat tersebut tidak terpenuhi lagi maka perulangan akan terhenti.
- 3. ’éŚ Persamaan : ’éŚ Iteratif dan rekursif merupakan metode atau teknik didalam perulangan(looping) ’éŚ Sama-sama memiliki bagian yang berfungsi sebagai batas dalam sebuah perulangan ’éŚ Perbedaan : Iteratif dalam melakukan perulangan membutuhkan suatu instruksi program seperti for, repeat until dan while do, sedangkan rekursi tidak memakai instruksi program seperti itu. Cukup dengan fungsi tersebut.
- 4. Contoh Penggunaan Proses Rekursif ’éŚ Masalah : Memotong roti tawar tipis-tipis sampai habis. ’éŚ Algoritma : 1. Jika roti sudah habis atau potongannya sudah paling tipis maka pemotongan roti selesai. 2. Jika roti masih bisa dipotong, potong tipis dari tepi roti tersebut. 3. Lakukan prosedur 1 dan 2 untuk sisa potongannya.
- 5. Contoh Fungsi Rekursif ’éŚ Fungsi Pangkat ’éŚ Faktorial ’éŚ Deret Fibonacci ’éŚ Menara Hanoi
- 6. Fungsi Pangkat ’éŚ Menghitung 10 pangkat n dengan menggunakan konsep rekursif. ’éŚ Secara notasi pemrograman dapat dituliskan sebagai berikut : 100 = 1.......................................(1) 10n = 10. 310n-1..............................(2) 10 = 10. 102 Contoh : 102 = 10. 101 101 = 10. 100 100 = 1
- 7. Faktorial ’éŚ 0!=1 ’éŚ N ! = N x (N-1) ! Untuk N > 0 ’éŚ Secara notasi pemrograman dapat dituliskan sebagai berikut : FAKT(0) = 1...................................(1) FAKT(N) = N * FAKT(N-1)................(2) Contoh : FAKT(5) = 5 * FAKT(4) FAKT(4) = 4 * FAKT(3) FAKT(3) = 3 * FAKT(2) FAKT (2) = 2 * FAKT(1) FAKT(1) = 1 * FAKT (0) Nilai awal;
- 8. ’éŚ Misal : Hitung 5 ! dapat dihitung dengan cara rekursif sebagai berikut : 5!=5*4! secara rekursif nilai dari 4 ! dapat dihitung kembali dengan cara : 4 * 3 ! sehingga 5 ! menjadi 5! = 5 * 4 * 3! secara rekursif nilai dari 3 ! dapat dihitung kembali dengan cara : 3 * 2 ! sehingga 5 ! menjadi 5! = 5 * 4 * 3 * 2 ! secara rekursif nilai dari 2 ! dapat dihitung kembali dengan cara : 2 * 1 sehingga 5 ! menjadi 5! = 5 * 4 * 3 * 2 * 1
- 9. Deret Fibonacci ’éŚ Deret Fibonacci : 0, 1, 1,2, 3, 5, 8, 13,... ’éŚ Secara notasi pemrograman dapat dituliskan sebagai berikut : FIBO (1) = 0 dan FIBO (2) = 1.....................(1) FIBO (N) = FIBO (N-1) + FIBO (N-2)............(2) Contoh : FIBO(5) = FIBO (4) + FIBO (3) FIBO (4) = FIBO(3) + FIBO (2) FIBO (3) = FIBO (2) + FIBO (1) Nilai Awal
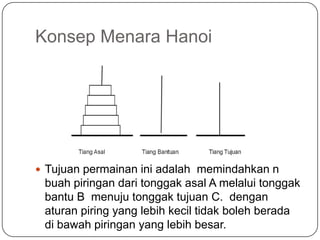
- 10. Konsep Menara Hanoi ’éŚ Tujuan permainan ini adalah memindahkan n buah piringan dari tonggak asal A melalui tonggak bantu B menuju tonggak tujuan C. dengan aturan piring yang lebih kecil tidak boleh berada di bawah piringan yang lebih besar.
- 11. ’éŚ Bayangkan keadaan berikut: Ada 3 tiang (a, b, c) tempat piringan dengan ukuran yang bervariasi dapat ditumpuk. Pada mulanya semua piringan ada di ŌĆ£aŌĆØ. Tugasnya adalah Memindah semua piringan ke ŌĆ£cŌĆØ dengan aturan sbb: ’éŚ pada satu saat hanya boleh memindah 1 piringan ’éŚ setiap perpindahan berupa pengambilan piringan teratas dari satu tiang dan memasukannya ketiang lain, diatas piringan lain yang mungkin sudah ada pada tiang tersebut. ’éŚ Tidak boleh meletakan piringan diatas piringan lain yang lebih kecil. (piringan yang lebih besar tidak boleh berada di atas piringan yang lebih kecil).
- 12. ’éŚ Dalam notasi algoritma dapat dituliskan sebagai berikut : ’éŚ Jika n = 1, maka langsung pindahkan saja piringan dari tiang A ke tiang C dan selesai. ’éŚ Pindahkan n- 1 piringan yang paling atas dari tiang A ke tiang B. ’éŚ Pindahkan piringan ke n ( piringan terakhir) dari tiang A ke tiang C. ’éŚ Pindahkan n-1 piringan dari tiang B ke tiang C.
- 13. ’éŚ Untuk Penyelesaian masalah kita daftarkan terlebih dahulu langkah-langkah penyelesaiannya: ’éŚ ketika kondisi piringan ’āĀ N= 1 Piringan 1 dipindahkan dari A ke C. ’éŚ N =2 Pindahkan piringan 1 dari A ke B Pindahkan piringan 2 dari A ke C Pindahkan piringan 1 dari B ke C
- 14. ’éŚ Langkah pemindahan tersebut di atas dapat diubah menjadi notasi sebagai berikut : Menara (n, asal, bantu, tujuan) ’āś Untuk jumlah piringan n > 1 dapat dibagi menjadi tiga notasi penyelesaian. ’āś Menara(n-1, asal, bantu, tujuan); ’āś Menara (n, asal, bantu, tujuan); atau asal ŌåÆ tujuan ’āś Menara (n, bantu, asal, tujuan);
- 15. Langkah Pemindahan Piring ’éŚ Menara (1, A, C, B).................AŌåÆ B ’éŚ Menara (2,A, B, C) AŌåÆ C......... AŌåÆ C ’éŚ Menara (1, B, A, C).................B ŌåÆ C ’éŚ Menara (3, A, C, B) AŌåÆ B......... AŌåÆ B ’éŚ Menara (1, C, B, A).................CŌåÆ A ’éŚ Menara (2, C, A, B)CŌåÆ B..........C ŌåÆ B ’éŚ Menara (1, A, C, B).................AŌåÆ B ’éŚ Menara (4, A, B, C) AŌåÆ C......... AŌåÆ C ’éŚ Menara (1, B, A, C).................BŌåÆ C ’éŚ Menara (2, B, C, A) BŌåÆ A.........BŌåÆ A ’éŚ Menara (1, C, B, A).................CŌåÆ A ’éŚ Menara (3, B, A, C) B ŌåÆ C....... BŌåÆ C ’éŚ Menara (1, A, C, B).................AŌåÆ B ’éŚ Menara (2, A, B, C) A ŌåÆ C ......AŌåÆ C ’éŚ Menara (1, B, A, C).................BŌåÆ C
- 16. ’éŚ Ilustrasi di atas menghasilkan 15 langkah penyelesaian dari permasalahan konsep menara Hanoi dengan jumlah piringan sebanyak 4 buah. ’éŚ Rumus Langkah Pemindahan : 2N ŌĆō1 N = jumlah piringan