Bab7 garis singgung lingkaran kelas8semester2 1
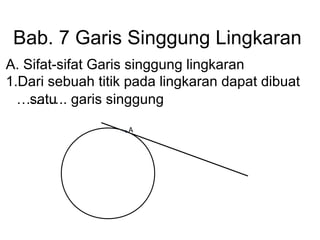
- 1. Bab. 7 Garis Singgung Lingkaran A. Sifat-sifat Garis singgung lingkaran 1.Dari sebuah titik pada lingkaran dapat dibuat ……… .. garis singgung satu A
- 2. 2.Dari sebuah titik di luar lingkaran dapat dibuat ……… .. garis singgung dua P
- 3. 3.Dua garis singgung lingkaran yang ditarik dari sebuah titik diluar lingkaran adalah sama panjang A B AP = BP P
- 4. 4.Garis singgung lingkaran tegak lurus dengan jari-jari atau diameter yang ditarik dari titik singgungnya A O
- 5. Definisi-definisi *Garis singgung lingkaran adalah……. suatu garis yang memotong lingkaran di satu titik **Garis singgung persekutuan adalah :….. Garis yang menyinggung dua lingkaran sekaligus Garis singgung persekutuan luar Garis singgung persekutuan dalam
- 6. *Layang-layang garis singgung adalah…. Segi empat yang dibentuk oleh dua garis singung lingkaran yang melalui satu titik di luar lingkaran dan dua jari-jari yang melalui titik singgung
- 7. *Kedudukan dua lingkaran yang berbeda 1. 2. A A B B
- 8. 3. 4. 5. 6. A A B A B A B A B
- 9. 1. 2. *Kemungkinan garis singgung pada dua lingkaran yang berbeda 4 2 A A B B
- 10. 3. 3 4. 1 A B A B
- 11. 5. Tidak punya garis singgung 6. A Tidak punya garis singgung A B A B
- 12. B. Menghitung panjang Garis singgung lingkaran O r T A AT 2 = OT 2 - r 2
- 13. Contoh soal : Sebuah lingkaran berdiameter 12 cm. Dan sebuah titik T diluar lingkaran yang berjarak 10 cm dari pusat lingkaran.Hitung berapa panjang garis singgung lingkaran dari titik T ! 6 cm 10 cm AT 2 = OT 2 - r 2 = 10 2 - 6 2 = 100 - 36 = 64 AT= 8 cm O T A
- 14. 2. Sebuah lingkaran berjari-jari 5cm. Panjang garis singgung lingkaran dari titik T diluar lingkaran adalah 12cm. Berapa jarak titik T ke pusat lingkaran? 5 cm 12 cm OT 2 = AT 2 + r 2 = 12 2 + 5 2 = 144 + 25 = 169 OT = 13 cm O T A
- 15. 3. Jarak pusat lingkaran o dan titik T diluar lingkaranadalah 15 cm. Panjang garis singgung lingkaran dari titik T diluar lingkaran adalah 12cm. Berapa jari-jari lingkaran o? 12 cm 15 cm r 2 = OT 2 - AT 2 = 15 2 – 12 2 = 225 - 144 = 81 r = 9 cm O T A
- 16. C. Menghitung panjang Garis singgung Persekutuan x DC 2 = AB 2 – x 2 DC 2 = AB 2 – (R-r) 2 DC = garis singgung persekutuan luar A B R r D C
- 17. C AC 2 = AB 2 – BC 2 KM 2 = AB 2 – (R+r) 2 KM = garis singgung persekutuan dalam A B R r K M
- 18. Contoh soal : Dua lingkaran saling lepas berjari-jari 8 cm dan 3 cm.Jarak kedua pusat lingkaran 13 cm. Tentukan panjang garis singgung persekutuan luar ? 13 DC 2 = AB 2 – (R-r) 2 DC 2 = 13 2 – (8-3) 2 DC 2 = 169 – 25 DC 2 = 144 DC = 12 cm garis singgung persekutuan luar = 12 cm A B R=8 R=3 D C
- 19. 2. Dua lingkaran saling lepas berjari-jari 4 cm dan 2 cm.Jarak kedua pusat lingkaran 10 cm. Tentukan panjang garis singgung persekutuan dalam? 10 KM 2 = AB 2 – (R+r) 2 KM 2 = 10 2 – (4+2) 2 KM 2 = 100 – 36 KM 2 = 64 KM = 8 cm garis singgung persekutuan dalam = 8 cm A B R=4 r = 2 K M