Bai9 caycanbang
- 1. CäËu trû¤c dã₤ liãu vû ThuäÙt toûÀn Tû˜m kiä¢m CûÂy áã- áen vû CûÀc cûÂy cûÂn bäÝng áãng khûÀc
- 2. Tû°m tä₤t ã CûÂy áã - áen (Red-Black) ã Mãt thuäÙt toûÀn phãˋc täÀp ã Cho O(log n) vãi Thûˆm(addition), Xû°a(deletion) vû Tû˜m(search) ã CûÀc kã¿ thuäÙt phäÏn mãm ã Biä¢t vã thuäÙt toûÀn ã Biä¢t khi nû o cû° thã dû¿ng chû¤ng ã Biä¢t vã hiãu suäËt ã Biä¢t nóÀi cû° thã ûÀp dãËng ã áÃ£Ï thûÇng minh áã dû¿ng cho cûÀc mûÀy phûÀt minh... ã Hã sã٠dãËng läÀi bã mûÈ ã Vû˜ thä¢ hã cäÏn nhiãu thãi gian hóÀn cho ã Chuyä¢n ái, án, uãng, ... BäËt cãˋ nhã₤ng gû˜ khûÀc mû tûÇi sä§ cho vû o áûÂy.
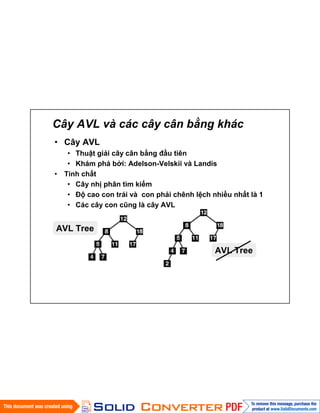
- 3. CûÂy AVL vû cûÀc cûÂy cûÂn bäÝng khûÀc ã CûÂy AVL ã ThuäÙt giäÈi cûÂy cûÂn bäÝng áäÏu tiûˆn ã KhûÀm phûÀ bãi: Adelson-Velskii vû Landis ã TûÙnh chäËt ã CûÂy nhã phûÂn tû˜m kiä¢m ã áã cao con trûÀi vû con phäÈi chûˆnh lãch nhiãu nhäËt lû 1 ã CûÀc cûÂy con céˋng lû cûÂy AVL AVL Tree AVL Tree
- 4. CûÂy AVL ã Chiãu cao ã áãnh lû§ ã Mãt cûÂy AVL cû° chiãu cao h cû° ûÙt nhäËt Fh+3+1 node ã Chãˋng minh ã áã Sh lû kûÙch cãÀ cãÏa cûÂy AVL nhã nhäËt vãi chiãu cao h ã Rûç rû ng, S0 = 1 and S1 = 2 ã HóÀn nã₤a, Sh = Sh-1 + Sh-2 + 1 ã Mãt cûÂy cû° chiãu cao cãÝc tiãu phäÈi bao gãp nhiãu cûÂy cû° chiãu cao nhã vãi áã lãch tãi áa lû 1 ã Do áû° .. ã Sh = Fh+3+1
- 5. CûÂy AVL ã Chiãu cao ã BûÂy giã, tãng quûÀt cho i, Fi+1 / Fi = , trong áû° = ô§(1 + 5) hoäñc Fi c (ô§(1 + 5))i ã Sh = Fh+3 + 1 = O( bh ) ã n Sh , vû˜ thä¢ n lû ( bh ) vû h logb n hoäñc h is O(log n)
- 6. CûÂy AVL ã Chiãu cao ã BûÂy giã, tãng quûÀt cho i, Fi+1 / Fi = , trong áû° = ô§(1 + 5) hoäñc Fi c (ô§(1 + 5))i ã Sh = Fh+3 + 1 = O( bh ) ã n Sh , vû˜ thä¢ n lû ( bh ) vû h logb n hoäñc h lû O(log n) ã Trong tró¯Ã£ng hãÈp nû y, chã ra ã h 1.44 logb (n+2) - 1.328 h khûÇng tãi hóÀn 44% cao hóÀn so vãi tãi ó¯u
- 7. CûÂy AVL ã TûÀi cûÂn bäÝng ã Chû´n cûÀc lûÀ vû o cûÂy non-AVL ã 4 tró¯Ã£ng hãÈp ã 1 vû 4 lû cûÀc äÈnh áãi xãˋng ã 2 vû 3 lû cûÀc äÈnh áãi xãˋng 1 2 3 4
- 8. CûÂy AVL ã TûÀi cûÂn bäÝng ã Tró¯Ã£ng hãÈp 1 áó¯Ã£Èc giäÈi bãi phûˋp quay ã Tró¯Ã£ng hãÈp 4 lû quay mãt äÈnh áãi xãˋng
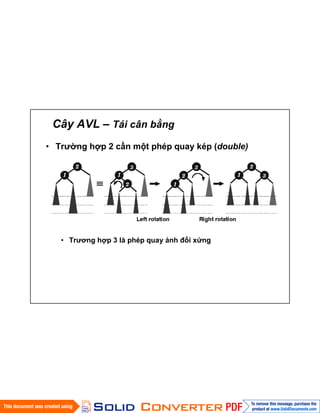
- 9. CûÂy AVL ã TûÀi cûÂn bäÝng ã Tró¯Ã£ng hãÈp 2 cäÏn mãt phûˋp quay kûˋp (double) ã Tró¯óÀng hãÈp 3 lû phûˋp quay äÈnh áãi xãˋng
- 10. CûÂy AVL ã CäËu trû¤c dã₤ liãu ã CûÀc cûÂy AVL cû° thã áó¯Ã£Èc thãÝc hiãn vãi mãt cã áã bûÀo hiãu träÀng thûÀi cûÂn bäÝng ã Chû´n (Insertion) ã Chû´n mãt node mãi (giãng bäËt cãˋ cûÂy nhã phûÂn nû o) ã Viãc cûÂn bäÝng läÀi cûÂy (duyãt ngó¯Ã£Èc lûˆn) cäÏn thiä¢t phãËc hãi cûÀc tûÙnh chäËt cãÏa AVL typedef enum { LeftHeavy, Balanced, RightHeavy } BalanceFactor; struct AVL_node { BalanceFactor bf; void *item; struct AVL_node *left, *right; }
- 11. CûÀc cûÂy áãng - Red-Black hoäñc AVL ã Chû´n (Insertion) ã AVL : hai bó¯Ã£c thãÝc hiãn trûˆn cûÂy ã Duyãt xuãng áã chû´n thûˆm node ã Duyãt lûˆn áã tûÀi cûÂn bäÝng (re-balance) ã Red-Black : hai bó¯Ã£c thãÝc hiãn trûˆn cûÂy ã Duyãt xuãng áã chû´n thûˆm node ã Duyãt lûˆn áã tûÀi cûÂn bäÝng (re-balance) nhó¯ng Red-Black phã biä¢n hóÀn??
- 12. CûÀc cûÂy áãng ã CäÈnh bûÀo ã Chû´n (Insertion) ã Nä¢u bäÀn áãc Cormen et al, ã KhûÇng cû° mãt lû§ do nû o áã thûÙch mãt cûÂy áã- áen ã Tuy nhiûˆn, trong sûÀch cãÏa Weiss M A Weiss, Algorithms, Data Structures and Problem Solving with C++, Addison-Wesley, 1996 ã BäÀn tû˜m thäËy räÝng bäÀn cû° thã cûÂn bäÝng cûÂy red-black Tãng kä¢t läÀi ! ã TäÀo mãt cûÂy red-black nhiãu hiãu quÃ¤È hóÀn AVL Nä¢u mûÈ code lû hãÈp lû§!!!
- 13. CûÀc cûÂy áãng ã CäÈnh bûÀo ã Chû´n (Insertion) ã Nä¢u bäÀn áãc Cormen et al, ã KhûÇng cû° mãt lû§ do nû o áã thûÙch mãt cûÂy áã- áen ã Tuy nhiûˆn, trong sûÀch cãÏa Weiss M A Weiss, Algorithms, Data Structures and Problem Solving with C++, Addison-Wesley, 1996 ã BäÀn tû˜m thäËy räÝng bäÀn cû° thã cûÂn bäÝng cûÂy red-black Tãng kä¢t läÀi ! ã TäÀo mãt cûÂy red-black nhiãu hiãu quÃ¤È hóÀn AVL Nä¢u mûÈ code lû hãÈp lû§!!! Yûˆu cäÏu: BäÀn cäÏn thiä¢t áãc cûÀc tû i liãu!
- 14. CûÀc cûÂy áãng ã CäÈnh bûÀo ã Tãng kä¢t cho ãchû´nã Insertion ã Khi bäÀn ái áä¢n phûÙa dó¯Ã£i cãÏa mãt cûÂy, nä¢u bäÀn tû˜m thäËy mãt node vãi hai con red, tûÇ nû° mû u red vû con cãÏa nû° mû u black ã áiãu nû y khûÇng biä¢n áãi sã ló¯Ã£Èng cûÀc node áen trong bäËt cãˋ nhûÀnh nû o ã Nä¢u cha cãÏa node lû mäÏu red, mãt phûˋp quay lû cäÏn thiä¢t ... ã Cû° thã cäÏn mãt phûˋp quay áóÀn hoäñc quay kûˋp
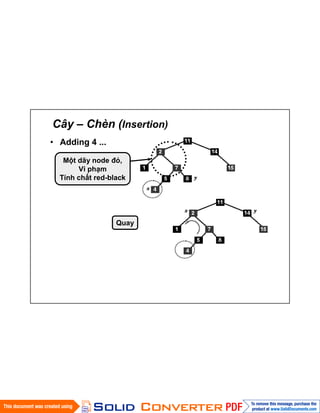
- 15. CûÂy ã Chû´n (Insertion) ã Adding 4 ... PhûÀt hiãn hai Con mû u áã ã áûÂy HoûÀn vã mû u cho nhau
- 16. CûÂy ã Chû´n (Insertion) ã Adding 4 ... Mãt dûÈy node áã, Vi phäÀm TûÙnh chäËt red-black Quay
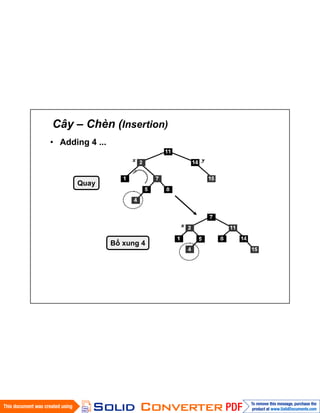
- 17. CûÂy ã Chû´n (Insertion) ã Adding 4 ... Quay Bã xung 4
- 18. CûÂy cûÂn bäÝng ã Chó¯a cû° nhiãu biä¢n áãi ã CóÀ bäÈn cû° cû¿ng cûÀc û§ tó¯Ã£ng ã 2-3 Trees ã 2-3-4 Trees ã Tró¯Ã£ng hãÈp däñc biãt cãÏa cûÂy m-way! ã Sã ló¯Ã£Èng cûÀc con cho mãt node biä¢n thiûˆn ThÃ£Ï tãËc thãÝc hiãn phãˋc täÀp hóÀn ã 2-3-4 trees ã Chiä¢u vã cûÂy red-black Cû° lä§ hã₤u dãËng khi hiãu mãt cûÂy red-black
- 19. Tãng kä¢t ã CûÂy AVL ã áäÏu tiûˆn lû cûÂy cûÂn bäÝng áãng ã Chiãu cao thuãc 44% so vãi áiãu kiãn thuäÙn lãÈi nhäËt ã TûÀi cûÂn bäÝng vãi cûÀc gû°c quay ã O(log n) ã Hiãu quÃ¤È thäËp hóÀn so vãi cûÂy red-black ã 2-3, 2-3-4 trees ã m-way trees ã chó¯a cû° nhiãu biä¢n áãi ã 2-3-4 trees áó¯Ã£Èc chiä¢u vã cûÂy red-black
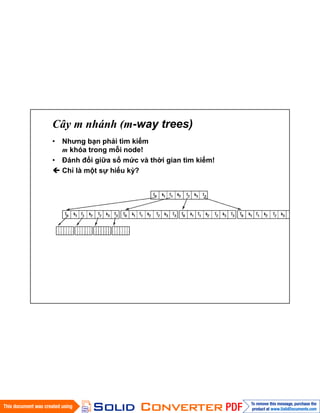
- 20. CûÂy m nhûÀnh (m-way trees) ã Chã hai con cho mãt node? ã Rû¤t gãn áã sûÂu cãÏa cûÂy áä¢n O(logmn) vãi m-way trees ã m con, m-1 khû°a cho node ã m = 10 : 106 khû°a trong 6 mãˋc khûÀc 20 cho cûÂy nhã phûÂn ã nhó¯ng ........
- 21. CûÂy m nhûÀnh (m-way trees) ã Nhó¯ng bäÀn phäÈi tû˜m kiä¢m m khû°a trong mãi node! ã áûÀnh áãi giã₤a sã mãˋc vû thãi gian tû˜m kiä¢m! Chã lû mãt sÃ£Ý hiä¢u kã°?
- 22. CûÂy B(Block) (B-trees) ã TäËt cÃ¤È cûÀc lûÀ näÝm trûˆn cû¿ng mãt mãˋc ã TäËt cÃ¤È cûÀc node ngoäÀi tr㨠gãc vû cûÀc lûÀ cû°: ã ût nhäËt m/2 con ã Nhiãu nhäËt m con ã CûÂy B+ (B+ trees) ã TäËt cÃ¤È cûÀc khû°a trong cûÀc node lû giÃ¤È ã Chã cûÀc khû°a trong cûÀc lûÀ nhäÙn giûÀ trã thãÝc ãrealã ã Liûˆn kä¢t cûÀc lûÀ ã Cû° khÃ¤È náng duyãt hä¢t danh sûÀch theo thãˋ tÃ£Ý giã₤a khûÇng cäÏn thûÇng qua cûÀc node cao hóÀn. Mãi node chãˋa ûÙt nhäËt mãt nãÙa sã ló¯Ã£Èng khû°a
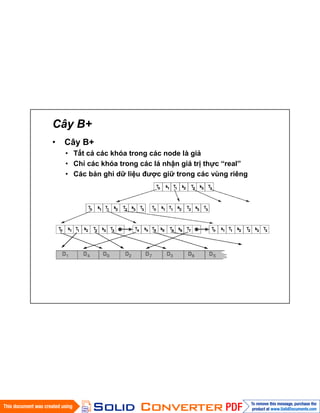
- 23. CûÂy B+ ã CûÂy B+ ã TäËt cÃ¤È cûÀc khû°a trong cûÀc node lû giÃ¤È ã Chã cûÀc khû°a trong cûÀc lûÀ nhäÙn giûÀ trã thãÝc ãrealã ã CûÀc bäÈn ghi dã₤ liãu áó¯Ã£Èc giã₤ trong cûÀc vû¿ng riûˆng
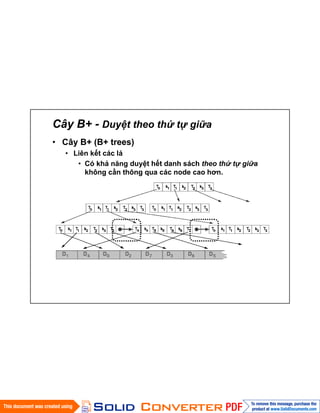
- 24. CûÂy B+ - Duyãt theo thãˋ tÃ£Ý giã₤a ã CûÂy B+ (B+ trees) ã Liûˆn kä¢t cûÀc lûÀ ã Cû° khÃ¤È náng duyãt hä¢t danh sûÀch theo thãˋ tÃ£Ý giã₤a khûÇng cäÏn thûÇng qua cûÀc node cao hóÀn.
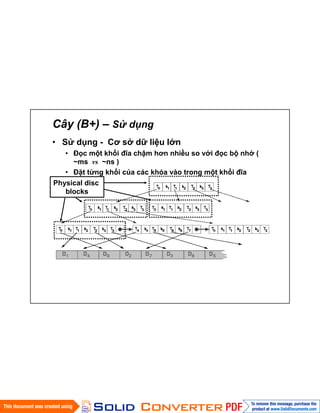
- 25. CûÂy (B+) ã Sã٠dãËng ã Sã٠dãËng - CóÀ sã dã₤ liãu lãn ã áãc mãt khãi ááˋa chäÙm hóÀn nhiãu so vãi áãc bã nhã ( ~ms vs ~ns ) ã áäñt tã¨ng khãi cãÏa cûÀc khû°a vû o trong mãt khãi ááˋa Physical disc blocks
- 26. CûÂy B (B-trees) - Chû´n ã Chû´n (Insertion) ã TûÙnh chäËt cûÂy B (B-tree): mãt khãi cû° ûÙt nhäËt mãt nã₤a sã khû°a ã Chû´n vû o trong khãi vãi m khû°a ã Trû n khãi ã PhûÂn tûÀch khãi ã áäˋy mãt khû°a ã PhûÂn tûÀch cha mä¿ nä¢u cäÏn thiä¢t ã Nä¢u gãc bã tûÀch, cûÂy áó¯Ã£Èc áäñt ã mãˋc sûÂu hóÀn
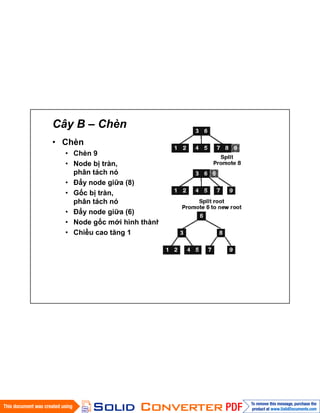
- 27. CûÂy B ã Chû´n ã Chû´n ã Chû´n 9 ã Node bã trû n, phûÂn tûÀch nû° ã áäˋy node giã₤a (8) ã Gãc bã trû n, phûÂn tûÀch nû° ã áäˋy node giã₤a (6) ã Node gãc mãi hû˜nh thû nh ã Chiãu cao táng 1
- 28. CûÂy B trûˆn ááˋa ã CûÀc khãi ááˋa ã 512 - 8k bytes 100s of keys Dû¿ng tû˜m kiä¢m nhã phûÂn cho cûÀc khãi ã Tãng quûÀt ã O( log n ) ã Lû m hãÈp vãi phäÏn cãˋng ! ã ThÃ£Ï tãËc xû°a tó¯óÀng tÃ£Ý (Deletion) ã Tuy nhiûˆn, phäÈi hãi nhäÙp cûÀc khãi (block) áã bäÈo áäÈm tûÙnh chäËt B-tree (ûÙt nhäËt bäÝng nãÙa sã ló¯Ã£Èng khû°a)