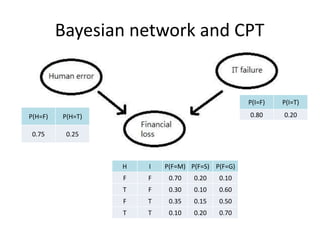
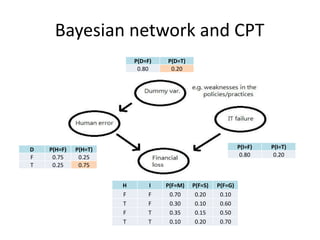
Bayesian network and cpt
- 1. P(H=F) P(H=T) 0.75 0.25 P(I=F) P(I=T) 0.80 0.20 H I P(F=M) P(F=S) P(F=G) F F 0.70 0.20 0.10 T F 0.30 0.10 0.60 F T 0.35 0.15 0.50 T T 0.10 0.20 0.70 Bayesian network and CPT
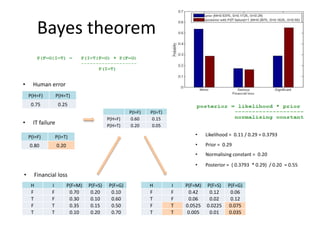
- 3. Bayes theorem H I P(F=M) P(F=S) P(F=G) F F 0.70 0.20 0.10 T F 0.30 0.10 0.60 F T 0.35 0.15 0.50 T T 0.10 0.20 0.70 • Financial loss P(H=F) P(H=T) 0.75 0.25 • Human error P(I=F) P(I=T) 0.80 0.20 • IT failure P(I=F) P(I=T) P(H=F) 0.60 0.15 P(H=T) 0.20 0.05 H I P(F=M) P(F=S) P(F=G) F F 0.42 0.12 0.06 T F 0.06 0.02 0.12 F T 0.0525 0.0225 0.075 T T 0.005 0.01 0.035 • Likelihood = 0.11 / 0.29 = 0.3793 • Normalising constant = 0.20 • Prior = 0.29 • Posterior = ( 0.3793 * 0.29) / 0.20 = 0.55
- 4. P(I=F) P(I=T) 0.80 0.20 D P(H=F) P(H=T) F 0.75 0.25 T 0.25 0.75 P(D=F) P(D=T) 0.80 0.20 H I P(F=M) P(F=S) P(F=G) F F 0.70 0.20 0.10 T F 0.30 0.10 0.60 F T 0.35 0.15 0.50 T T 0.10 0.20 0.70 Bayesian network and CPT
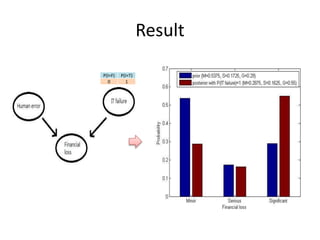
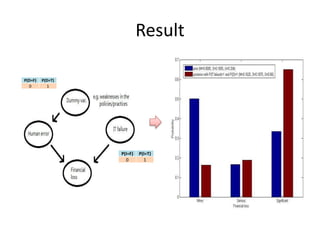
- 5. Result P(D=F) P(D=T) 0 1 P(I=F) P(I=T) 0 1