Bellmanford
- 1. Chapter 4 Network Layer Computer Networking: A Top Down Approach Featuring the Internet , 2 nd edition. Jim Kurose, Keith Ross Addison-Wesley, July 2002. A note on the use of these ppt slides: We’re making these slides freely available to all (faculty, students, readers). They’re in powerpoint form so you can add, modify, and delete slides (including this one) and slide content to suit your needs. They obviously represent a lot of work on our part. In return for use, we only ask the following: If you use these slides (e.g., in a class) in substantially unaltered form, that you mention their source (after all, we’d like people to use our book!) If you post any slides in substantially unaltered form on a www site, that you note that they are adapted from (or perhaps identical to) our slides, and note our copyright of this material. Thanks and enjoy! JFK/KWR All material copyright 1996-2002 J.F Kurose and K.W. Ross, All Rights Reserved
- 2. Distance Vector Routing Algorithm (Bellman Ford) iterative: continues until no nodes exchange info. self-terminating : no “signal” to stop asynchronous: nodes need not exchange info/iterate in lock step! distributed: each node communicates only with directly-attached neighbors Distance Table data structure each node has its own row for each possible destination column for each directly-attached neighbor to node example: in node X, for dest. Y via neighbor Z: D (Y,Z) X distance from X to Y, via Z as next hop c(X,Z) + min {D (Y,w)} Z w = =
- 3. Distance Table: example 7 8 1 2 1 2 loop! loop! A E D C B D () A B C D A 1 7 6 4 B 14 8 9 11 D 5 5 4 2 E cost to destination via destination D (C,D) E c(E,D) + min {D (C,w)} D w = = 2+2 = 4 D (A,D) E c(E,D) + min {D (A,w)} D w = = 2+3 = 5 D (A,B) E c(E,B) + min {D (A,w)} B w = = 8+6 = 14
- 4. Distance table gives routing table A B C D A,1 D,5 D,4 D,4 Outgoing link to use, cost destination Distance table Routing table D () A B C D A 1 7 6 4 B 14 8 9 11 D 5 5 4 2 E cost to destination via destination
- 5. Distance Vector Routing: overview Iterative, asynchronous: each local iteration caused by: local link cost change message from neighbor: its least cost path change from neighbor Distributed: each node notifies neighbors only when its least cost path to any destination changes neighbors then notify their neighbors if necessary Each node: wait for (change in local link cost of msg from neighbor) recompute distance table if least cost path to any dest has changed, notify neighbors
- 6. Distance Vector Algorithm: 1 Initialization: 2 for all adjacent nodes v: 3 D (*,v) = infinity /* the * operator means "for all rows" */ 4 D (v,v) = c(X,v) 5 for all destinations, y 6 send min D (y,w) to each neighbor /* w over all X's neighbors */ X X X w At all nodes, X:
- 7. Distance Vector Algorithm (cont.): 8 loop 9 wait (until I see a link cost change to neighbor V 10 or until I receive update from neighbor V) 11 12 if (c(X,V) changes by d) 13 /* change cost to all dest's via neighbor v by d */ 14 /* note: d could be positive or negative */ 15 for all destinations y: D (y,V) = D (y,V) + d 16 17 else if (update received from V wrt destination Y) 18 /* shortest path from V to some Y has changed */ 19 /* V has sent a new value for its min DV(Y,w) */ 20 /* call this received new value is "newval" */ 21 for the single destination y: D (Y,V) = c(X,V) + newval 22 23 if we have a new min D (Y,w)for any destination Y 24 send new value of min D (Y,w) to all neighbors 25 26 forever w X X X X X w w
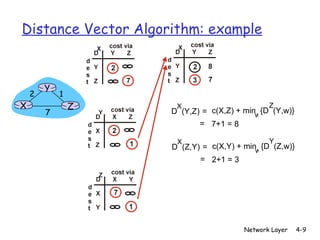
- 8. Distance Vector Algorithm: example X Z 1 2 7 Y
- 9. Distance Vector Algorithm: example X Z 1 2 7 Y D (Y,Z) X c(X,Z) + min {D (Y,w)} w = = 7+1 = 8 Z D (Z,Y) X c(X,Y) + min {D (Z,w)} w = = 2+1 = 3 Y
- 10. Distance Vector: link cost changes Link cost changes: node detects local link cost change updates distance table (line 15) if cost change in least cost path, notify neighbors (lines 23,24) 1 4 50 1 algorithm terminates “ good news travels fast” X Z Y
- 11. Distance Vector: link cost changes Link cost changes: good news travels fast bad news travels slow - “count to infinity” problem! 1 4 50 60 algorithm continues on! X Z Y
- 12. Distance Vector: poisoned reverse If Z routes through Y to get to X : Z tells Y its (Z’s) distance to X is infinite (so Y won’t route to X via Z) will this completely solve count to infinity problem? 1 4 50 60 algorithm terminates X Z Y
- 13. Comparison of LS and DV algorithms Message complexity LS: with n nodes, E links, O(nE) msgs sent each DV: exchange between neighbors only convergence time varies Speed of Convergence LS: O(n 2 ) algorithm requires O(nE) msgs may have oscillations DV : convergence time varies may be routing loops count-to-infinity problem Robustness: what happens if router malfunctions? LS: node can advertise incorrect link cost each node computes only its own table DV: DV node can advertise incorrect path cost each node’s table used by others error propagate thru network
- 14. Chapter 4 roadmap 4.1 Introduction and Network Service Models 4.2 Routing Principles 4.3 Hierarchical Routing 4.4 The Internet (IP) Protocol 4.5 Routing in the Internet 4.6 What’s Inside a Router 4.7 IPv6 4.8 Multicast Routing 4.9 Mobility
- 15. Hierarchical Routing scale: with 200 million destinations: can’t store all dest’s in routing tables! routing table exchange would swamp links! administrative autonomy internet = network of networks each network admin may want to control routing in its own network Our routing study thus far - idealization all routers identical network “flat” … not true in practice
- 16. Hierarchical Routing aggregate routers into regions, “autonomous systems” (AS) routers in same AS run same routing protocol “ intra-AS” routing protocol routers in different AS can run different intra-AS routing protocol special routers in AS run intra-AS routing protocol with all other routers in AS also responsible for routing to destinations outside AS run inter-AS routing protocol with other gateway routers gateway routers
- 17. Intra-AS and Inter-AS routing Gateways: perform inter-AS routing amongst themselves perform intra-AS routers with other routers in their AS inter-AS, intra-AS routing in gateway A.c network layer link layer physical layer a b a C A B d b a A.a A.c C.b B.a c b c
- 18. Intra-AS and Inter-AS routing Host h2 Intra-AS routing within AS A Intra-AS routing within AS B We’ll examine specific inter-AS and intra-AS Internet routing protocols shortly a b b a a C A B d c A.a A.c C.b B.a c b Host h1 Inter-AS routing between A and B