Benson-ASRANET2012
- 1. COMPARTMENT LEVEL PROGRESSIVE COLLAPSE ANALYSIS OF A LIGHTWEIGHT HULL GIRDER Simon Benson, Jonathan Downes and Robert S. Dow School of Marine Science and Technology
- 2. 2 Contents  Motivation  The Smith Progressive Collapse Method  The Extended Progressive Collapse Method  Case Study – Aluminium Multihull  Conclusions
- 3. 3 Motivation  Office of Naval Research (ONR) project: “Structural Performance of Lightweight Naval Vessels”  Development and extension of hull girder progressive collapse analysis methodologies:  Ultimate Strength Analysis  Limit State Design  Optimisation  Reliability  Damage Strength  Recoverability  Evaluation of longitudinal bending capacity of the hull girder  Solution methods:  Simplified Progressive Collapse Analysis  Nonlinear Finite Element Analysis
- 4. Motivation  Established hull girder progressive collapse methods have been developed primarily for STEEL ships.  How do we adapt these approaches to lightweight ships?  Two general approaches:  Simplified analytical methods (e.g. progressive collapse):  Fast and efficient  Simplifying assumptions  Implicit characterisation of material and geometric imperfections  Nonlinear finite element methods (FEM):  Computationally expensive  Requires explicit characterisation of all material and geometric properties in the FE model  Which methods are suitable for reliability analysis?
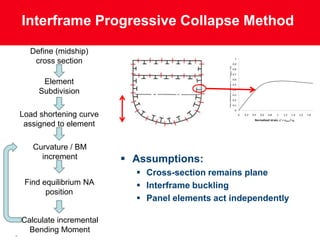
- 5. Interframe Progressive Collapse Method 5083-H116 Plate Load Shortening Curves Define (midship) HAZ Ratio (HR) = 8 cross section 1 0.9 Normalised Stress, s' = save / s0 0.8 0.7 Element 0.6 0.5 b=2 Subdivision 0.4 0.3 0.2 0.1 0 Load shortening curve 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 Normalised strain, e' = e ave / e 0 assigned to element Curvature / BM increment  Assumptions:  Cross-section remains plane 1.50 Bending Moment, Mx (N.mm) x 10-10 1.00 Find equilibrium NA  Interframe buckling 0.50 position hog  Panel elements act independently 0.00 sag -0.50 Progressive Collapse - 150mm hard corners Abaqus 5bay model (50mm element size) -1.00 Calculate incremental Abaqus 5bay model (25mm element size) -1.50 Bending Moment -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00 Curvature, C (1/mm) x 106
- 6. Extended Progressive Collapse Method Define (midship) cross section  Extends the approach used to define the Element element behaviour Subdivision  Revised Assumptions:  Cross section remains plane (as before) Load shortening curve  Compartment level elements assigned to element  Elements do not act independently  Interframe and overall buckling properties Curvature / BM combined increment Find equilibrium NA position Calculate incremental Bending Moment
- 7. 7 Extended Progressive Collapse Method Element Definition  Standard approach:  Plate-stiffener combination elements  Hard corners  Each element assigned a load shortening curve (LSC)  Element does not have to correspond directly to LSC  Refine for accuracy in calculations  LSC can represent global elements  LSC can be calculated for:  Components (plates, stiffeners)  Plate-stiffener combinations  Orthogonal stiffened panels  Panel strength calculated by a semi analytical orthotropic plate method
- 8. 8 Extended Progressive Collapse Method Panel Load Shortening Curves  Derived using a semi analytical method  Increments of end strain/displacement  At each increment: 1. Evaluate component (plate and stiffener) resistance 2. Calculate combined resistance 3. Evaluate beam column (interframe) strength and compare 4. Evaluate panel (overall) strength and compare 5. Derive increment of load shortening curve  Panel strength derived using a large deflection orthotropic plate method  Method uses instantaneous component stiffness properties  Panel LSC can be assigned to small elements
- 9. 9 Extended Progressive Collapse Method Implementation - ProColl  A GUI Interface for the extended progressive collapse method  Interframe and compartment level analyses  Runs vertical bending or combinations of vertical and horizontal (interaction diagram)  Increments of curvature or bending moment  Post processor capabilities  Generate element load shortening curves  Process BM vs. curvature plots  Graphically display element stiffness and NA position
- 10. Case Study: Aluminium Multihull
- 11. Case Study: Aluminium Multihull
- 12. 12 Case Study: Aluminium Multihull Interframe Analysis  Interframe LSCs  Close correlation to equivalent FEM
- 13. Case Study: Aluminium Multihull Interframe Analysis  Sag Bending Moment  Interframe Results  Very close agreement between FEM and PColl
- 14. 14 Case Study: Aluminium Multihull Compartment Analysis  Top Deck LSC  Overall Buckling  Reduction in ultimate strength  Close agreement between FEM and semi analytical method
- 15. Case Study: Aluminium Multihull Compartment Analysis  7 bay results:  reduction in ultimate strength  Buckling of top deck prior to ultimate strength point  Buckling of second deck at ultimate strength point  Close agreement between FEM and PColl  Top Deck Load Shortening Curve:  Accounts for different longitudinal stiffener sizes
- 16. Case Study: Aluminium Multihull 16
- 17. 17 Conclusions  We propose an extended progressive collapse methodology  Utilises a semi analytical method to predict compartment level load shortening curves  Case study progressive collapse assessment of an aluminium multihull is presented:  Shows significant strength reduction due to compartment level buckling  Good correlation to FEM results  Both FEM and simplified methods can produce reasonable and valid solutions for the compartment level progressive collapse problem