狠狠撸

1
正規分布の背景
Kobe.R #5
2014.06.14
@florets1

2
正規分布
?
?
?
?
?
?
??= 2
22/12
2
)(
2
1
exp
)2(
1
),( ?
σπσ
σ? xN

3
正規分布はあちこちに現れる
測定値の分布
熱の拡散

4
今回お話すること
日常のいろいろなところに現れる正規分布
他の分布に比べて何かが特別な感じがしませんか？
実は正規分布とは
情報量の平均（エントロピー）が最大になる分布なんです。

5
驚きの度合い（情報量）を測ろう
A 起こりそうもないことが起きた。
B いつでも起きそうなことが起きた。
A の情報量 > B の情報量

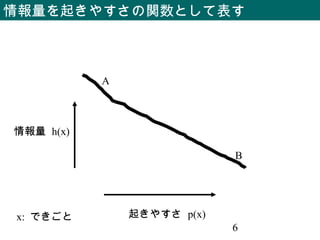
6
情報量を起きやすさの関数として表す
起きやすさ p(x)
情報量 h(x)
x: できごと
A
B

7
情報量は足し算できてほしい
h(x, y) = h(x) + h(y)
x, y: できごと
例えばトランプを引くとき
h(x): ハートが出た場合の情報量
h(y): エースが出た場合の情報量
h(x,y): ハートのエースが出た場合の情報量

8
２つの無関係なできごとは統計的に独立
p(x, y) = p(x) p(y)
x, y: できごと

9
以上より情報量 h(x) をこのように定義する
p(x)
h(x)
h(x, y) = h(x) + h(y)
p(x, y) = p(x) p(y)
)(log)( xpxh ?=

10
底は何でもよい
)(log)( 2 xpxh ?=
)(ln)( xpxh ?=
底が 2 の場合、 h(x) の単位は bit

11
エントロピー　情報量の平均
)(log)(][ xpxpxH
x
∑?=
dxxpxpxH )(log)(][ ∫?=
離散確率変数 x の場合
連続確率変数 x の場合

12
エントロピーの性質
bitxH 2
64
1
log
64
4
16
1
log
16
1
8
1
log
8
1
4
1
log
4
1
2
1
log
2
1
][ 22222 =?????=
x の 8 個の状態それぞれの確率が
{1/2,1/4,1/8,1/16,1/64,1/64,1/64,1/64} の場合のエントロピー
bitxH 3
8
1
log
8
1
8][ 2 =×?=
x が 8 個の状態を等確率で取る場合のエントロピー

13
エントロピーの性質
データ分析者の観点だと
エントロピーが大きい→面白みのない退屈なデータだな。
エントロピーが小さい→面白い。何かが起こっていそうだ。

14
エントロピーが最大となる確率分布（離散）
離散確率変数 x の場合は一様分布
)(log)(][ xpxpxH
x
∑?=
1)( =∑x
xp制約条件
求め方
のもとで
を最大化する。

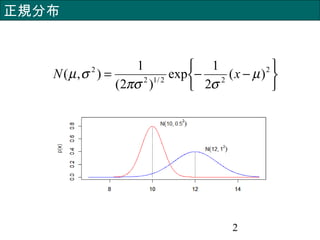
15
連続確率変数 x の場合は正規分布
∫ =1)( dxxp制約条件
求め方
のもとで
を最大化する。
∫ = ?dxxxp )(
∫ =? 22
)()( σ? dxxpx
dxxpxpxH )(log)(][ ∫?=
エントロピーが最大となる確率分布（連続）

16
まとめ
正規分布の正体は
エントロピーが最大となる連続分布だった。
やっぱり特別だった。
データ分析者にとってはエントロピーは小さいほうが面白い。
例えば正規分布に従う値動きの株があるとする。
その株を買いたいですか？
正規分布に従っていないデータに注目すべし。

17
参考文献
C.M. ビショップパターン認識と機械学習　上
平岡和幸?堀玄プログラミングのための确率统计

狠狠撸

Bgnd kobe.r5

More Related Content

Bgnd kobe.r5