Matematika Ekonomi - Biaya Marginal
- 1. MATEMATIKA EKONOMI Kelompok 5 1. Sonya Eki Santoso (4101412035) 2. Gema Fatahillah (4101412126)
- 2. ’é¦ Biaya Produksi dan Penerimaan (Marginal Cost dan Marginal Revenue) ’é¦ Keuntungan Produsen ’é¦ Pasar Persaingan Sempurna PEMBAHASAN
- 3. BIAYA PRODUKSI BIAYA PRODUKSI Biaya Tetap Total (Total Fixed Cost) Biaya Variabel Total (Total Variabel Cost) Biaya Total (Total Cost) Nilai dari faktor-faktor produksi (sumber-sumbr ekonomi) yang digunakan dalam proses produksi.
- 4. BIAYA TETAP TOTAL (tfc) tfc Jumlah biaya-biaya yang besarnya tetap, berapapun tingkat output yang dihasilkan. Contoh : penyusutan, sewa gudang, asuransi dan sebagainya.
- 5. BIAYA VARIABEL TOTAL (tVc) tVc Biaya yang besarnya tergantung dari jumlah output yang dihasilkan. Biaya variabel ini akan bertambah besar bila output yang dihasilkan bertambah, karena output yang lebih memerlukan faktor produksi yang lebih banyak Contoh : bahan mentah, upah, ongkos angkut dan sebagainya.
- 6. BIAYA TOTAL (TOTAL COST) tc Biaya Total (Total Cost) disingkat TC adalah jumlah dari biaya tetap dan biaya variabel. Øæ╗Øæ¬ = Øæ╗ØæŁØæ¬ + Øæ╗ØæĮØæ¬
- 7. Di samping konsep biaya total tersebut di atas, dipakai juga beberapa konsep biaya persatuan, yaitu: a. Biaya Tetap Rata-rata (Average Fixed Cost) b. Biaya Variabel Rata-rata (Average Variabel Cost) c. Biaya Total Rata-rata (Average Total Cost) d. Biaya Marjinal (Marginal Cost)
- 8. BIAYA TETAP RATA-RATA AFc Ongkos tetap yang dibebankan pada setiap unit output. Øæ©ØæŁØæ¬ = Øæ╗ØæŁØæ¬ ØæĖ
- 9. BIAYA VARIABEL RATA-RATA AV c Semua biaya-biaya lain, selain AFC yang dibebankan pada setiap unit output. Øæ©ØæĮØæ¬ = Øæ╗ØæĮØæ¬ ØæĖ
- 10. BIAYA TOTAL RATA-RATA Ac Biaya total yang dibebankan pada setiap unit output yang diproduksi. Øæ©Øæ¬ = Øæ╗Øæ¬ ØæĖ
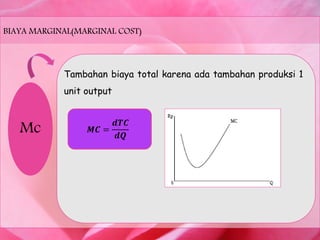
- 11. BIAYA MARGINAL(MARGINAL COST) Mc Tambahan biaya total karena ada tambahan produksi 1 unit output Øæ┤Øæ¬ = ØÆģØæ╗Øæ¬ ØÆģØæĖ
- 12. CONTOH Bila fungsi biaya rata-rata ditunjukkan oleh persamaan ØÉ┤ØÉČ = 25 ŌłÆ 8Øæä + Øæä2 tentukan biaya marjinalnya (MC)! Solusi : Untuk mendapatkan MC, maka langkah pertama adalah mencari TC-nya dulu. ØÉ┤ØÉČ = ØæćØÉČ Øæä Ō¤║ ØæćØÉČ = Øæä. ØÉ┤ØÉČ ØæćØÉČ = Øæä(25 ŌłÆ 8Øæä + Øæä2) = 25Øæä ŌłÆ 8Øæä2 + Øæä3 Kemudia kita cari MC ØæĆØÉČ = ØææØæćØÉČ ØææØæä = Øææ 25Øæä ŌłÆ 8Øæä2 + Øæä3 ØææØæä = 25 ŌłÆ 16Øæä + 3Øæä2
- 13. CONTOH Bila fungsi biaya rata-rata ditunjukkan oleh persamaan ØÉ┤ØÉČ = 25 ŌłÆ 8Øæä + Øæä2 . Tentukan jumlah output yang diproduksi pada saat AC minimum. Solusi : AC minimum terjadi bila ØææØÉ┤ØÉČ ØææØæä = 0 ØææØæÄØæø Øææ2 ØÉ┤ØÉČ ØææØæä2 > 0 ØææØÉ┤ØÉČ ØææØæä = 0 = ŌłÆ8 + 2Øæä 2Øæä = 8 Ō¤║ Øæä = 4 Untuk Øæä = 4 , Øææ2 ØÉ┤ØÉČ ØææØæä2 = 2 > 0 Jadi pada Øæä = 4 , maka AC minimum.
- 14. PENERIMAAN PENERIMAAN (REVENUE) Penerimaan Total (Total Revenue) Penerimaan Rata-Rata (Average Revenue) Penerimaan Marginal (Marginal Revenue) Penerimaan (revenue) adalah penerimaan produsen dari hasil penjualan outputnya.
- 15. PENERIMAAN TOTAL (tR) tR Penerimaan total produsen dari hasil penjualan outputnya. Penerimaan total merupakan hasil kali output dengan harga jual outputnya. Øæ╗Øæ╣ = ØæĘ. ØæĖ
- 16. CONTOH 1 Bila harga suatu barang Rp 100,00 per unit dan jumlah yang dijual adalah 50. Maka penerimaannya adalah : ØæćØæģ = Øæā. Øæä = 100. 50 = 5000 Jadi penerimaannya adalah Rp 5000,00
- 17. PENERIMAAN RATA-RATA (AR) AR Penerimaan produsen per unit outputnya yang dijual. Dari penjabaran di atas, terlihat bahwa penerimaan rata-rata besarnya sama dengan harga barang tersebut. Øæ©Øæ╣ = Øæ╗Øæ╣ ØæĖ = ØæĖ. ØæĘ ØæĖ ØæĖ = ØæĘ
- 18. CONTOH 2 Dari contoh 1 diatas, ØæćØæģ = ØæģØæØ 5000,00 dan Øæä = 50 Maka AR nya adalah : ØÉ┤Øæģ = ØæćØæģ Øæä = 5000 50 = 100 (harga barang/unit) Jadi penerimaan rata-ratanya adalah Rp 100,00
- 19. PENERIMAAN MARGINAL (MR) MR Tambahan penerimaan karena adanya tambahan penjualan satu unit output. Øæ┤Øæ╣ = ØÆģØæ╗Øæ╣ ØÆģØæĖ
- 20. KEUNTUNGAN PRODUSEN Karena keuntungan maksimum yang menjadi tujuannya, maka ia akan menentukan tingkat output (Q) yang dapat memberikan keuntungan yang maksimum. Posisi di mana output yang dihasilkan telah memberikan keuntungan maksimum ini dikatakan sebagai posisi keseimbangan (equilibrium). PRODUSEN MEMPRODUKSI BARANG KEUNTUNGAN MAKSIMUM
- 21. KEUNTUNGAN PRODUSEN KEU NTU NGA N Keuntungan merupakan selisih antara seluruh penerimaan dan ongkos-ongkos yang harus dikeluarkan oleh produsen. Ket : ØØģ : keuntungan TR : penerimaan TC : biaya . ØØģ = Øæ╗Øæ╣ ŌłÆ Øæ╗Øæ¬
- 22. KEUNTUNGAN PRODUSEN Keuntungan yang diperoleh akan maksimum apabila dipenuhi syarat : 1. ØÆģØØģ ØÆģØæĖ = Ø¤Ä 2. ØÆģ Ø¤É ØØģ ØÆģ Ø¤É ØæĖ < ؤÄ
- 23. CONTOH Bila penerimaan total produsen ditunjukkan oleh persamaan ØæćØæģ = 100Øæä ŌłÆ 4Øæä2 dan biaya totalnya ditunjukkan oleh persamaan ØæćØÉČ = 50 + 20Øæä maka tentukan jumlah output yang harus diproduksi agar supaya produsen memperoleh keuntungan yang maksimum. Solusi : Ø£ŗ = ØæćØæģ ŌłÆ ØæćØÉČ = 100Øæä ŌłÆ 4Øæä2 ŌłÆ 50 + 20Øæä = 100Øæä ŌłÆ 20Øæä ŌłÆ 4Øæä2 ŌłÆ 50 = 80Øæä ŌłÆ 4Øæä2 ŌłÆ 50
- 24. CONTOH Ø£ŗ akan maksimum bila : 1. ØææØ£ŗ ØææØæä = 0 Øææ 80Øæä ŌłÆ 4Øæä2 ŌłÆ 50 dQ = 0 Ō¤║ 80 ŌłÆ 8Øæä = 0 Ō¤║ 8Øæä = 80 Ō¤║ Øæä = 10 2. Øææ2 Ø£ŗ Øææ2 Øæä < 0 Øææ2 Ø£ŗ Øææ2 Øæä = Øææ 80 ŌłÆ 8Øæä ØææØæä = ŌłÆ8 < 0 Jadi, Øæä = 10 memberikan keuntungan yang maksimum.
- 25. PASAR PERSAINGAN SEMPURNA Pasar persaingan sempurna antara lain ditandai oleh banyaknya produsen dan konsumen sehingga masing-masing pihak baik itu produsen (penjual) dan konsumen tidak dapat mempengaruhi harga di pasar. Harga ditentukan oleh 'pasar'. Dalam pasar persaingan sempurna, kurva permintaan yang dihadapi oleh seorang produsen merupakan garis lurus horisontal. Ini berarti produsen dapat menjual outputnya dalam jumlah berapapun tanpa mengakibatkan terjadinya penurunan harga jual.
- 26. CONTOH Dalam pasar persaingan sempurna, fungsi permintaan ditunjukan oleh persamaan Øæā = 10. Penerimaan totalnya ØæćØæģ = Øæā. Øæä = 100Øæä Penerimaan rata-rata ØÉ┤Øæģ = ØæćØæģ Øæä = Øæā. Øæä Øæä = Øæā = 10 Penerimaan Marjinal ØæĆØæģ = ØææØæćØæģ ØææØæä = 10 Jadi dalam pasar persaingan sempurna fungsi permintaan berhimpit dengan fungsi penerimaan rata-rata dan penerimaan marjinalnya.
- 27. TERIMA KASIH