Bilangan biner
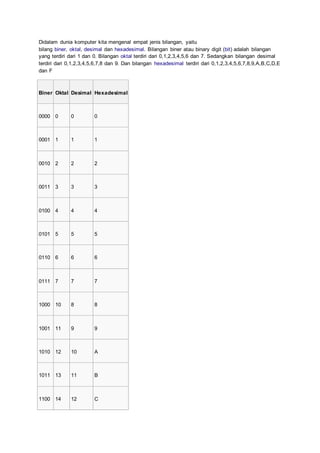
- 1. Didalam dunia komputer kita mengenal empat jenis bilangan, yaitu bilang biner, oktal, desimal dan hexadesimal. Bilangan biner atau binary digit (bit) adalah bilangan yang terdiri dari 1 dan 0. Bilangan oktal terdiri dari 0,1,2,3,4,5,6 dan 7. Sedangkan bilangan desimal terdiri dari 0,1,2,3,4,5,6,7,8 dan 9. Dan bilangan hexadesimal terdiri dari 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E dan F Biner Oktal Desimal Hexadesimal 0000 0 0 0 0001 1 1 1 0010 2 2 2 0011 3 3 3 0100 4 4 4 0101 5 5 5 0110 6 6 6 0111 7 7 7 1000 10 8 8 1001 11 9 9 1010 12 10 A 1011 13 11 B 1100 14 12 C
- 2. 1101 15 13 D 1110 16 14 E 1111 17 15 F Konversi Antar Basis Bilangan Sudah dikenal, dalam bahasa komputer terdapat empat basis bilangan. Keempat bilangan itu adalah biner, oktal, desimal dan hexadesimal. Keempat bilangan itu saling berkaitan satu sama lain. Rumus atau cara mencarinya cukup mudah untuk dipelajari. Konversi dari desimal ke non-desimal, hanya mencari sisa pembagiannya saja. Dan konversi dari non-desimal ke desimal adalah: 1. Mengalikan bilangan dengan angka basis bilangannya. 2. Setiap angka yang bernilai satuan, dihitung dengan pangkat NOL (0). Digit puluhan, dengan pangkat SATU (1), begitu pula dengan digit ratusan, ribuan, dan seterusnya. Nilai pangkat selalu bertambah satu point. [sunting]Konversi Biner ke Oktal Metode konversinya hampir sama. Cuma, karena pengelompokkannya berdasarkan 3 bit saja, maka hasilnya adalah: 1010 (2) = ...... (8) Solusi: Ambil tiga digit terbelakang dahulu. 010(2) = 2(8)Sedangkan sisa satu digit terakhir, tetap bernilai 1. Hasil akhirnya adalah: 12. [sunting]Konversi Biner ke Hexadesimal Metode konversinya hampir sama dengan Biner ke Oktal. Namun pengelompokkannya sejumlah 4 bit. Empat kelompok bit paling kanan adalah posisi satuan, empat bit kedua dari kanan adalah puluhan, dan seterusnya. Contoh: 11100011(2) = ...... (16) Solusi: kelompok bit paling kanan: 0011 = 3 kelompok bit berikutnya: 1110 = E Hasil konversinya adalah: E3(16) [sunting]Konversi Biner ke Desimal Cara atau metode ini sedikit berbeda. Contoh: 10110(2) = ......(10) diuraikan menjadi: (1x24)+(0x23)+(1x22)+(1x21)+(0x20) = 16 + 0 + 4 + 2 + 0 = 22 Angka 2 dalam perkalian adalah basis biner-nya. Sedangkan pangkat yang berurut, menandakan pangkat 0 adalah satuan, pangkat 1 adalah puluhan, dan seterusnya. [sunting]Konversi Oktal ke Biner Sebenarnya, untuk konversi basis ini, haruslah sedikit menghafal tabel konversi utama yang berada di halaman atas. Namun dapat dipelajari dengan mudah. Dan ambillah tiga biner saja. Contoh: 523(8) = ...... (2) Solusi: Dengan melihat tabel utama, didapat hasilnya adalah: 3 = 011 2 = 010 5 = 101 Pengurutan bilangan masih berdasarkan posisi satuan, puluhan dan ratusan. Hasil:101010011(2) [sunting]Konversi Hexadesimal ke Biner Metode dan caranya hampir serupa dengan konversi Oktal ke Biner. Hanya pengelompokkannya sebanyak dua bit. Seperti pada tabel utama. Contoh: 2A(16) = ......(2)
- 3. Solusi:  A = 1010,  2 = 0010 caranya: A=10  10:2=5(0)-->sisa  5:2=2(1)  2:2=1(0)  1:2=0(1) ditulis dari hasil akhir hasil :1010  2:2=1(0)-->sisa  1:2=0(1) ditulis dari hasil akhir hasil:010 jadi hasil dan penulisannya 0101010 sebagai catatan angka 0 diawal tidak perlu di tulis. [sunting]Konversi Desimal ke Hexadesimal Ada cara dan metodenya, namun bagi sebagian orang masih terbilang membingungkan. Cara termudah adalah, konversikan dahulu dari desimal ke biner, lalu konversikan dari biner kehexadesimal. Contoh: 75(10) = ......(16) Solusi: 75 dibagi 16 = 4 sisa 11 (11 = B). Dan hasil konversinya: 4B(16) [sunting]Konversi Hexadesimal ke Desimal Caranya hampir sama seperti konversi dari biner ke desimal. Namun, bilangan basisnya adalah 16. Contoh: 4B(16) = ......(10) Solusi: Dengan patokan pada tabel utama, B dapat ditulis dengan nilai "11". (4x161)+(11x160) = 64 + 11 = 75(10) [sunting]Konversi Desimal ke Oktal Caranya hampir sama dengan konversi desimal ke hexadesimal. Contoh: 25(10) = ......(8) Solusi: 25 dibagi 8 = 3 sisa 1. Hasilnya dapat ditulis: 31(8) 25 : 8 sisa 1 3 -------- 3 hasilnya adalah 31 [sunting]Konversi Oktal ke Desimal Metodenya hampir sama dengan konversi hexadesimal ke desimal. Dapat diikuti dengan contoh di bawah ini: 764(8) = ......(10) Solusi: (3x81)+(1x80) = 24 + 1 = 25(10)

![1101 15 13 D
1110 16 14 E
1111 17 15 F
Konversi Antar Basis Bilangan
Sudah dikenal, dalam bahasa komputer terdapat empat basis bilangan. Keempat bilangan itu
adalah biner, oktal, desimal dan hexadesimal. Keempat bilangan itu saling berkaitan satu sama lain.
Rumus atau cara mencarinya cukup mudah untuk dipelajari. Konversi dari desimal ke non-desimal,
hanya mencari sisa pembagiannya saja. Dan konversi dari non-desimal ke desimal adalah:
1. Mengalikan bilangan dengan angka basis bilangannya.
2. Setiap angka yang bernilai satuan, dihitung dengan pangkat NOL (0). Digit puluhan, dengan
pangkat SATU (1), begitu pula dengan digit ratusan, ribuan, dan seterusnya. Nilai pangkat selalu
bertambah satu point.
[sunting]Konversi Biner ke Oktal
Metode konversinya hampir sama. Cuma, karena pengelompokkannya berdasarkan 3 bit saja, maka
hasilnya adalah: 1010 (2) = ...... (8) Solusi: Ambil tiga digit terbelakang dahulu. 010(2) = 2(8)Sedangkan
sisa satu digit terakhir, tetap bernilai 1. Hasil akhirnya adalah: 12.
[sunting]Konversi Biner ke Hexadesimal
Metode konversinya hampir sama dengan Biner ke Oktal. Namun pengelompokkannya sejumlah 4
bit. Empat kelompok bit paling kanan adalah posisi satuan, empat bit kedua dari kanan adalah
puluhan, dan seterusnya. Contoh: 11100011(2) = ...... (16) Solusi: kelompok bit paling kanan: 0011 = 3
kelompok bit berikutnya: 1110 = E Hasil konversinya adalah: E3(16)
[sunting]Konversi Biner ke Desimal
Cara atau metode ini sedikit berbeda. Contoh: 10110(2) = ......(10) diuraikan menjadi:
(1x24)+(0x23)+(1x22)+(1x21)+(0x20) = 16 + 0 + 4 + 2 + 0 = 22 Angka 2 dalam perkalian adalah
basis biner-nya. Sedangkan pangkat yang berurut, menandakan pangkat 0 adalah satuan,
pangkat 1 adalah puluhan, dan seterusnya.
[sunting]Konversi Oktal ke Biner
Sebenarnya, untuk konversi basis ini, haruslah sedikit menghafal tabel konversi utama yang berada
di halaman atas. Namun dapat dipelajari dengan mudah. Dan ambillah tiga biner saja. Contoh:
523(8) = ...... (2) Solusi: Dengan melihat tabel utama, didapat hasilnya adalah: 3 = 011 2 = 010 5 = 101
Pengurutan bilangan masih berdasarkan posisi satuan, puluhan dan ratusan. Hasil:101010011(2)
[sunting]Konversi Hexadesimal ke Biner
Metode dan caranya hampir serupa dengan konversi Oktal ke Biner. Hanya pengelompokkannya
sebanyak dua bit. Seperti pada tabel utama. Contoh: 2A(16) = ......(2)](https://image.slidesharecdn.com/bilanganbiner-150118211541-conversion-gate02/85/Bilangan-biner-2-320.jpg)
![Solusi:
 A = 1010,
 2 = 0010
caranya: A=10
 10:2=5(0)-->sisa
 5:2=2(1)
 2:2=1(0)
 1:2=0(1)
ditulis dari hasil akhir
hasil :1010
 2:2=1(0)-->sisa
 1:2=0(1)
ditulis dari hasil akhir
hasil:010
jadi hasil dan penulisannya 0101010 sebagai catatan angka 0 diawal tidak perlu di tulis.
[sunting]Konversi Desimal ke Hexadesimal
Ada cara dan metodenya, namun bagi sebagian orang masih terbilang membingungkan. Cara
termudah adalah, konversikan dahulu dari desimal ke biner, lalu konversikan
dari biner kehexadesimal. Contoh: 75(10) = ......(16) Solusi: 75 dibagi 16 = 4 sisa 11 (11 = B). Dan hasil
konversinya: 4B(16)
[sunting]Konversi Hexadesimal ke Desimal
Caranya hampir sama seperti konversi dari biner ke desimal. Namun, bilangan basisnya adalah 16.
Contoh: 4B(16) = ......(10) Solusi: Dengan patokan pada tabel utama, B dapat ditulis dengan nilai "11".
(4x161)+(11x160) = 64 + 11 = 75(10)
[sunting]Konversi Desimal ke Oktal
Caranya hampir sama dengan konversi desimal ke hexadesimal. Contoh: 25(10) = ......(8) Solusi: 25
dibagi 8 = 3 sisa 1. Hasilnya dapat ditulis: 31(8)
25 : 8 sisa 1 3 -------- 3 hasilnya adalah 31
[sunting]Konversi Oktal ke Desimal
Metodenya hampir sama dengan konversi hexadesimal ke desimal. Dapat diikuti dengan contoh di
bawah ini: 764(8) = ......(10) Solusi: (3x81)+(1x80) = 24 + 1 = 25(10)](https://image.slidesharecdn.com/bilanganbiner-150118211541-conversion-gate02/85/Bilangan-biner-3-320.jpg)