BILANGAN BULAT
- 1. BILANGAN BULAT Operasi Hitung Bilangan Bulat Pangkat dan Akar Bilangan Bulat Mengenal Bilangan Bulat Sifat-sifat Operasi Hitung Bilangan Bulat
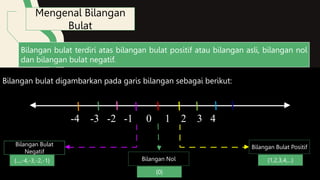
- 2. Mengenal Bilangan Bulat Bilangan bulat terdiri atas bilangan bulat positif atau bilangan asli, bilangan nol dan bilangan bulat negatif. Bilangan bulat digambarkan pada garis bilangan sebagai berikut: -4 -3 -2 -1 0 1 2 3 4 Bilangan Bulat Negatif Bilangan Bulat Positif Bilangan Nol {...,-4,-3,-2,-1} {0} {1,2,3,4,...}
- 3. Bilangan Bulat Bilangan Cacah Bilangan Asli Bilangan Genap Bilangan Ganjil Bilangan Prima Bilangan cacah adalah bilangan yang dimulai dari angka nol (0) sampai dengan tak terhingga. Contoh: 0,1,2,3,4,5,6,7,8,9,10,11.... dst Bilangan Asli adalah bilangan bulat positif yang dimulai dengan angka satu (1) sampai tak terhingga. Contoh: 1,2,3,4,5,67,8,9,10,11,... dst Bilangan Genap adalah bilangan bulat yang habis dibagi dua. Contoh: 2,4,6,8,10,12,14......dst Bilangan Ganjil adalah bilangan bulat yang tidak habis dibagi dua. Contoh: 1,3,5,7,9,11,13,15.....dst Bilangan Prima adalah bilangan yang hanya dapat dibagi oleh angka 1 atau bilangan itu sendiri. Contoh: 2,3,5,7,... dst
- 4. Bilangan bulat Positif maju Nol diam Negatif mundur Operasi tambah terus kurang balik arah
- 5. Operasi Hitung Bilangan Bulat 1. Penjumlahan Penjumlahan dua bilangan bulat bertanda sama Penjumlahan ini tejadi jika kedua bilangan memiliki tanda yang sama yaitu sama-sama bilangan positif dan sama-sama bilangan negatif. a + b = a + b (-a) + (-b) = -(a + b) Berlaku: 2 + 3 = ... Contoh 1 0 -1 2 -2 3 -3 4 -4 5 -5 3 2
- 6. (-2) + (-3) = ... 1 0 -1 2 -2 3 -3 4 -4 5 -5 3 -2 -(2+3) = -(5)
- 7. (-3) + (-5) = -(3+5) = -(8) (-5) + (-2) = -(5+2) = -(7) (-7) + (-15) = -(7+15) = - (22)
- 8. Penjumlahan dua bilangan bulat tanda berlawanan Penjumlahan ini terjadi jika kedua bilangan berbeda tandanya, yang satu bertanda positif, yang lainnya bertanda negatif. -a + b = b a a + (- b) = a b Berlaku: (-2) + 3 = ... Contoh 1 0 -1 2 -2 3 -3 4 -4 5 -5 3 -2 3 - 2 = 1
- 9. 2 + (-3) = ... 1 0 -1 2 -2 3 -3 4 -4 5 -5 3 2 2 - 3 = -1
- 10. (-10) + 7 = 7 - 10 = -3 (-15) + 20 = 20 - 15 = 5 2 + (-8) = 2 - 8 = -6
- 11. 1 0 -1 2 -2 3 -3 4 -4 5 -5 Jadi, 2 3 = 1 Hitung 2 3 Hitung 2 + (3) 2. Pengurangan a - b = a + (-b) a - (-b) = a + b Berlaku: Contoh
- 12. 1 0 -1 2 -2 3 -3 4 -4 5 -5 3 Jadi, 2 (3 ) = 2 + 3 = 5 2 Hitung 2 (3) = 2 + 3
- 13. 3 (-18) = 3 + 18 = 21 4 (-9) = 4 + 9 = 13 29 - (-10) = 29 + 10 = 39
- 14. Perkalian merupakan penjumlahan secara berulang. contoh: 3 x 5 = 5 + 5 + 5 = 15 a x b = ab a x ( b) = - ab (-a) x b = - ab (-a) x (-b) = ab Berlaku: 3. Perkalian 5 x 6 = 30 4 x (-7) = - 28 (-3) x 4 = -12 (-6) x (-7) = 42 Contoh Perkalian merupakan kebalikan/invers dari perkalian. contoh: 30 : 5 = 30 1 5 = 6 a : b = a : ( b) = - (-a) : b = - (-a) : (-b) = Berlaku: 4. Pembagian 5 x 6 = 30 4 x (-7) = - 28 (-3) x 4 = -12 (-6) x (-7) = 42 Contoh
- 15. Sifat-sifat Operasi Hitung Bilangan Bulat a + b = b + a 4 + 2 = 2 + 4 Penjumlah an 1. Sifat Komutatif (pertukaran) 2. Sifat Asosiatif (pengelompokan) Perkalian a x b = b x a 4 x 2 = 2 x 4 a + (b + c) = (a + b) + c 4 + ( 5 + 6) = ( 4 + 5 ) + 6 = 15 Penjumlah an Perkalian a x (b x c ) = (a x b) x c 4 x (5 x 6) = ( 4 x 5) x 6 = 120
- 16. 3. Sifat Distributif (penyebaran) a x (b + c ) = (a x b ) + ( a x c ) 2 x ( 3 + 4 ) = (2 x 3 ) + ( 2 x 4 ) = 14 Pada operasi perkalian terhadap penjumlahan Pada operasi perkalian terhadap pengurangan a x (b - c ) = (a x b ) - ( a x c ) 5 x ( 7 - 6 ) = (5 x 7 ) - ( 5 x 6 ) = 5
- 17. Pangkat dan Akar Bilangan Bulat Kuadrat Bilangan Bulat (Pangkat dua) Diperoleh dengan mengalikan bilangan itu dengan bilangan itu sendiri, atau mengalikan bilangan tersebut secara berulang sebanyak dua kali. 2 = contoh : 42 = 4 4 = 16 (9)2= 9 9 = 81 1. Kuadrat dan Pangkat Tiga Bilangan Bulat Pangkat Tiga Bilangan Bulat Diperoleh dengan mengalikan bilangan tersebut secara berulang sebanyak tiga kali. 3 = contoh : 63 = 6 6 6 = 216 (5)3= 5 5 5 = 25 5 = 125
- 18. Akar Kuadrat Merupakan kebalikan dari kuadrat (pangkat dua). Lambangnya (akar pangkat dua) contoh : 49 = 賊 7, karena 72 = 49 dan (7)2= 49 121 = 賊 11 karena 112 = 121 dan (-11)2 = 121 2. Akar Kuadrat dan Akar Pangkat Tiga Akar Pangkat Tiga Merupakan kebalikan dari pangkat tiga. Lambangnya (akar pangkat tiga) contoh : 27 = 3, karena 33 = 27 125 = 5, karena 53 = 125