Binary heap (Priority Queue).ppt
- 1. 1 Priority Queues Supports the following operations. ? Insert element x. ? Return min element. ? Return and delete minimum element. Applications. ? Dijkstra's shortest path algorithm. ? Prim's MST algorithm. ? Event-driven simulation. ? Huffman encoding. ? Heapsort. ? . . .
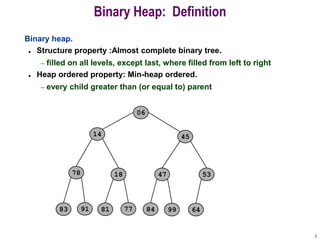
- 2. 2 Binary Heap: Definition Binary heap. ? Structure property :Almost complete binary tree. ¨C filled on all levels, except last, where filled from left to right ? Heap ordered property: Min-heap ordered. ¨C every child greater than (or equal to) parent 06 14 78 18 81 77 91 45 53 47 64 84 99 83
- 3. 3 Binary Heap: Properties Properties. ? Min element is in root. ? Heap with N elements has height = ?log2 N?. 06 14 78 18 81 77 91 45 53 47 64 84 99 83 N = 14 Height = 3
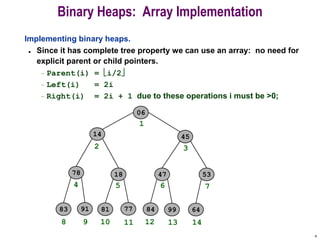
- 4. 4 Binary Heaps: Array Implementation Implementing binary heaps. ? Since it has complete tree property we can use an array: no need for explicit parent or child pointers. ¨C Parent(i) = ?i/2? ¨C Left(i) = 2i ¨C Right(i) = 2i + 1 due to these operations i must be >0; 06 14 78 18 81 77 91 45 53 47 64 84 99 83 1 2 3 4 5 6 7 8 9 10 11 12 13 14
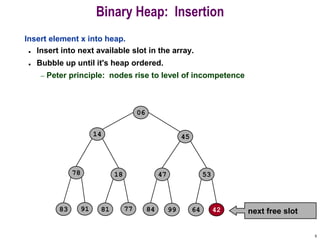
- 5. 5 Binary Heap: Insertion Insert element x into heap. ? Insert into next available slot in the array. ? Bubble up until it's heap ordered. ¨C Peter principle: nodes rise to level of incompetence 06 14 78 18 81 77 91 45 53 47 64 84 99 83 42 next free slot
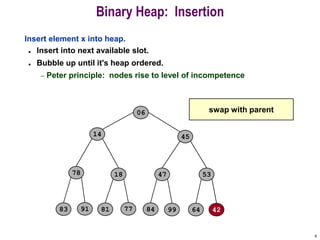
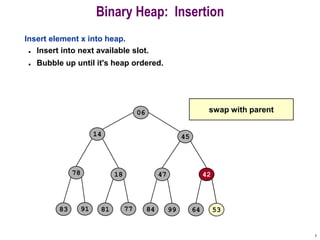
- 6. 6 Binary Heap: Insertion Insert element x into heap. ? Insert into next available slot. ? Bubble up until it's heap ordered. ¨C Peter principle: nodes rise to level of incompetence 06 14 78 18 81 77 91 45 53 47 64 84 99 83 42 42 swap with parent
- 7. 7 Binary Heap: Insertion Insert element x into heap. ? Insert into next available slot. ? Bubble up until it's heap ordered. 06 14 78 18 81 77 91 45 42 47 64 84 99 83 42 53 swap with parent
- 8. 8 Binary Heap: Insertion Insert element x into heap. ? Insert into next available slot. ? Bubble up until it's heap ordered is satisfied. (percolate up) ¨C Peter principle: nodes rise to level of incompetence ? O(log N) operations. 06 14 78 18 81 77 91 42 45 47 64 84 99 83 53 stop: heap ordered
- 9. 9 Binary Heap: Insertion 1. First increase the heap size by 1, so that it can store the new element. 2. Insert the new element at the end of the Heap. 3. This newly inserted element may violate the heap order property of Heap. 4. So, in order to keep the properties of Heap, percolate- up this newly inserted element following a bottom-up approach. Percolate up procedure/ Heapify operation i) Compare the value of this child node inserted with its parent. ii) If the value of parent is less than child, then swap them. iii) Repeat step i) & ii) until Heap order property is satisfied
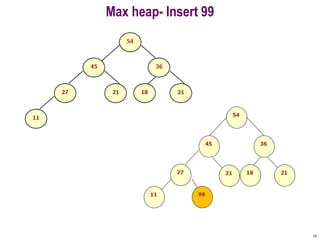
- 10. Max heap- Insert 99 10 45 36 27 21 18 21 11 54 99
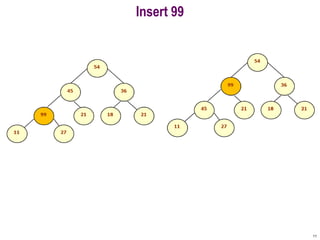
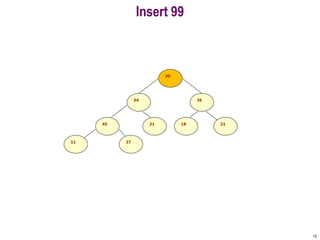
- 11. Insert 99 11
- 12. Insert 99 12 54 36 45 21 18 21 11 99 27
- 13. 13 Binary Heap: Insertion void insert(MinHeap heap, int x) { if ( hsize<capacity) //check heap full { hsize=hsize+1; int ctnode=hsize; While(ctnode!=1 && heap[ctnode/2]>x) {//shiftup heap[ctnode]=heap[ctnode/2]; //move the empty hole up ctnode=ctnode/2; } heap[ctnode]=x; } }
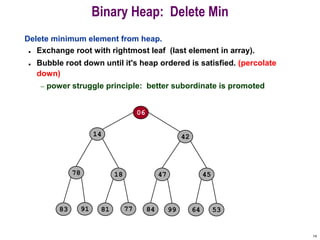
- 14. 14 Binary Heap: Delete Min Delete minimum element from heap. ? Exchange root with rightmost leaf (last element in array). ? Bubble root down until it's heap ordered is satisfied. (percolate down) ¨C power struggle principle: better subordinate is promoted 06 14 78 18 81 77 91 42 45 47 64 84 99 83 53
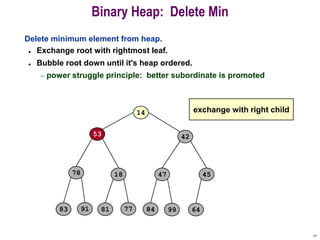
- 15. 15 Binary Heap: Delete Min Delete minimum element from heap. ? Exchange root with rightmost leaf. ? Bubble root down until it's heap ordered. ¨C power struggle principle: better subordinate is promoted 53 14 78 18 81 77 91 42 45 47 64 84 99 83 06
- 16. 16 Binary Heap: Delete Min Delete minimum element from heap. ? Exchange root with rightmost leaf. ? Bubble root down until it's heap ordered. ¨C power struggle principle: better subordinate is promoted 53 14 78 18 81 77 91 42 45 47 64 84 99 83 exchange with left child
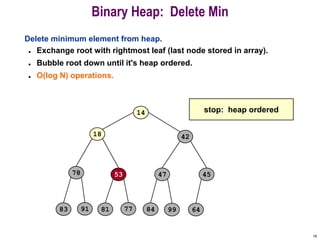
- 17. 17 Binary Heap: Delete Min Delete minimum element from heap. ? Exchange root with rightmost leaf. ? Bubble root down until it's heap ordered. ¨C power struggle principle: better subordinate is promoted 14 53 78 18 81 77 91 42 45 47 64 84 99 83 exchange with right child
- 18. 18 Binary Heap: Delete Min Delete minimum element from heap. ? Exchange root with rightmost leaf (last node stored in array). ? Bubble root down until it's heap ordered. ? O(log N) operations. 14 18 78 53 81 77 91 42 45 47 64 84 99 83 stop: heap ordered
- 19. 19 Binary Heap: Delete min 1. Replace the root or element to be deleted by the last element in the last level. 2. Delete the last element from the Heap. 3. Since, the last element is now placed at the position of the root node. So, it may not follow the heap order property. 4. Therefore, Percolate-down the last node placed at the position of root. Percolate down procedure/ Heapify operation i) Compare the value of this parent node with its minimum child. ii) If the value of parent is greater than minimum child, then swap them. iii) Repeat step i) & ii) until Heap order property is satisfied
- 20. 20 Binary Heap: Delete min void delete min(minheap heap) { if ( hsize>0) //check if empty { int lastelement=heap[hsize]; hsize=hsize-1; //shift down the hole int ctnode=1; int child=2;
- 21. 21 Binary Heap: Delete min While(child<hsize) { if ( (child<hsize) && heap[child]>heap[child+1] child=child+1; //right child is min child //else left child is the minimum child if (lastelement <= heap[child]) break; heap[ctnode]=heap[child]; ctnode=child; child=ctnode*2; } heap[ctnode]=lastelement; } }
Editor's Notes
- Event driven simulation: generate random inter-arrival times between customers, generate random processing times per customer, Advance clock to next event, skipping intervening ticks
- parent and children formula require only simple bit twiddling operations




![13
Binary Heap: Insertion
void insert(MinHeap heap, int x)
{ if ( hsize<capacity) //check heap full
{ hsize=hsize+1;
int ctnode=hsize;
While(ctnode!=1 && heap[ctnode/2]>x)
{//shiftup
heap[ctnode]=heap[ctnode/2];
//move the empty hole up
ctnode=ctnode/2;
}
heap[ctnode]=x;
} }](https://image.slidesharecdn.com/binaryheappriorityqueue-230604122801-fbc8e199/85/Binary-heap-Priority-Queue-ppt-13-320.jpg)



![20
Binary Heap: Delete min
void delete min(minheap heap)
{
if ( hsize>0) //check if empty
{ int lastelement=heap[hsize];
hsize=hsize-1;
//shift down the hole
int ctnode=1;
int child=2;](https://image.slidesharecdn.com/binaryheappriorityqueue-230604122801-fbc8e199/85/Binary-heap-Priority-Queue-ppt-20-320.jpg)
![21
Binary Heap: Delete min
While(child<hsize)
{
if ( (child<hsize) && heap[child]>heap[child+1]
child=child+1; //right child is min child
//else left child is the minimum child
if (lastelement <= heap[child])
break;
heap[ctnode]=heap[child];
ctnode=child;
child=ctnode*2;
}
heap[ctnode]=lastelement;
}
}](https://image.slidesharecdn.com/binaryheappriorityqueue-230604122801-fbc8e199/85/Binary-heap-Priority-Queue-ppt-21-320.jpg)