Lecture 9: Binary tree basics
•Download as PPTX, PDF•
2 likes•810 views
Binary trees are data structures where every node has at most two children, a left and right child. A binary tree has a root node at the top and leaf nodes at the bottom with no children. The depth of a node is the length of the path from the root to that node, while the height is the length of the longest path between the root and a leaf plus one. Binary trees can be full, complete, or fully complete depending on how nodes are distributed. Common operations on binary trees include searching, summing nodes, and traversing them in inorder, preorder, or postorder sequences.
![Vector
vector<int> a;
a.push_back(value);
cout<<a[i]<<endl;
Accessing the pushed back value similar to an
array.(REST READ FROM NET)](https://image.slidesharecdn.com/binarytreebasics-140904065840-phpapp02/85/Lecture-9-Binary-tree-basics-20-320.jpg)
Lecture 9: Binary tree basics
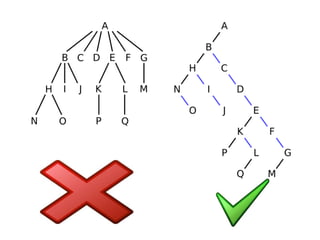
- 2. Binary Tree Definition • Every node has at most two children a left child and a right child. • Root - the top most node in a tree.
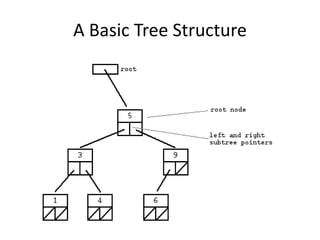
- 4. A Basic Tree Structure
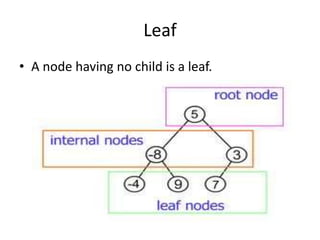
- 5. Leaf • A node having no child is a leaf.
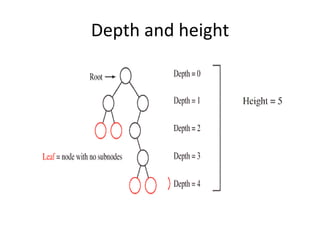
- 6. Depth of a node • The length of the path from the root to the node. • Depth(root)=0
- 7. Height of the tree • The height of a node is the length of the longest downward path between the node and a leaf + 1. • The height of a node is the length of the longest downward path between the root and a leaf +1.
- 9. Full Binary Tree • Every node has 2 children except the leaves.
- 10. Complete Binary Tree • A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
- 11. • A fully complete binary tree has n nodes what is the height of the tree?
- 12. • A fully complete binary tree has n nodes what are the number of leaves in the tree?
- 13. Implementation
- 14. Search an element in binary tree
- 15. Sum of all the nodes of the tree
- 16. Inorder traversal • Visit the left subtree first • Visit the node. • Visit the right subtree.
- 17. Code
- 18. Postorder traversal • Visit the left subtree first • Visit the right subtree • Visit the node.
- 19. Preorder traversal • Visit the node. • Visit the left subtree first • Visit the right subtree.
- 20. Vector vector<int> a; a.push_back(value); cout<<a[i]<<endl; Accessing the pushed back value similar to an array.(REST READ FROM NET)
- 21. Oj.leetcode.com https://oj.leetcode.com/problems/binary-tree-postorder- traversal/ https://oj.leetcode.com/problems/binary-tree-preorder- traversal/ https://oj.leetcode.com/problems/balanced-binary- tree/ https://oj.leetcode.com/problems/balanced-binary- tree/
- 22. • https://oj.leetcode.com/problems/binary-tree-level- order-traversal/ • https://oj.leetcode.com/problems/binary-tree-level- order-traversal/ • https://oj.leetcode.com/problems/binary-tree-inorder- traversal/ • https://oj.leetcode.com/problems/construct-binary- tree-from-inorder-and-postorder-traversal/ • https://oj.leetcode.com/problems/construct-binary- tree-from-preorder-and-inorder-traversal/