Boundary layer theory 3
Download as pptx, pdf1 like510 views
The document discusses boundary layer theory and the Von Karman Momentum Integral Equation. It explains that according to the continuity equation for steady incompressible fluid flow, the mass rate of flow entering two sections plus the mass rate leaving another section must be equal. It also states that the rate of change of momentum in a control volume is equal to the momentum flux through three surfaces minus the momentum flux entering and leaving other surfaces, according to the momentum integral equation.
1 of 11
Downloaded 20 times










Ad
Recommended
Boundary layer theory 1
Boundary layer theory 1sistec
?
This document provides an introduction to boundary layer theory in fluid mechanics. It defines key terms like boundary layer thickness, displacement thickness, and momentum thickness. The boundary layer is a thin region near a solid surface where velocity gradients exist due to no-slip conditions. As fluid flows over a plate, the boundary layer transitions from laminar to turbulent flow. Boundary layer theory divides fluid flow into the boundary layer region with velocity gradients and an external region with nearly uniform free stream velocity.Types of fluid flow best ppt
Types of fluid flow best pptPRATHAMESH DESHPANDE
?
The document provides an overview of various types of fluid flow, defining key characteristics such as steady and unsteady, compressible and incompressible, and laminar and turbulent flow. It explains important concepts like aerodynamic force, cavitation, and the distinctions between different flow types including Couette flow and free molecular flow. Additionally, it discusses the implications of these flow types in various applications such as aerospace and fluid dynamics.Fluid Mechanics Chapter 6. Boundary Layer Concept
Fluid Mechanics Chapter 6. Boundary Layer ConceptAddisu Dagne Zegeye
?
This document provides an overview of boundary layer concepts and laminar and turbulent pipe flow. It defines boundary layer thickness, displacement thickness, and momentum thickness. It describes how boundary layers develop on surfaces and transition from laminar to turbulent. It also discusses Reynolds number effects, momentum integral estimates for flat plates, and examples calculating boundary layer thickness in air and water flow. Finally, it introduces concepts of laminar and turbulent pipe flow.Flow through pipes
Flow through pipesvaibhav tailor
?
This document provides an overview of fluid mechanics concepts related to flow through pipes. It discusses different types of head losses that can occur through pipes including major losses due to friction and minor losses due to fittings. It also covers topics such as hydraulic grade line, pipes in series and parallel, syphons, power transmission through pipes, flow through nozzles, and water hammer effects in pipes.Boundary layer theory
Boundary layer theorySanmitaVarma
?
This document discusses boundary layer theory, which defines a thin layer of fluid near a solid boundary where viscosity is dominant. Ludwig Prandtl first proposed this theory in 1904 to model fluid flow. The boundary layer has different regions and is classified as laminar or turbulent. Key terms like displacement thickness, momentum thickness, and energy thickness are also defined. Boundary layer separation can occur in adverse pressure gradients and examples are given. Methods to prevent separation are outlined. The theory has applications in aerodynamics, heat transfer, and other fluid flow problems.Turbulent flow
Turbulent flowDarshit Panchal
?
This document provides an overview of turbulent fluid flow, including:
1) It defines laminar and turbulent flow and explains that turbulent flow occurs above a Reynolds number of 2000.
2) It describes methods for characterizing turbulence, including magnitude, intensity, and mixing length theory.
3) It discusses the universal law of the wall and how velocity is distributed in smooth and rough pipes. Friction factors depend on Reynolds number and relative roughness.
4) Experimental results from Nikuradse are presented showing relationships between friction factor and Reynolds number/relative roughness that can be used to model pressure losses in pipes.Boundary layer theory
Boundary layer theoryManthan Chavda
?
This document discusses boundary layer development. It begins by defining boundary layers and describing the velocity profile near a surface. As distance from the leading edge increases, the boundary layer thickness grows due to viscous forces slowing fluid particles. The boundary layer then transitions from laminar to turbulent. Turbulent boundary layers have a logarithmic velocity profile and thicker boundary layer compared to laminar. Pressure gradients and surface roughness also impact boundary layer development and transition.Fm ppt
Fm pptmanishdadhich8
?
This document discusses fluid flow through circular conduits and pipes. It covers topics such as laminar and turbulent flow, Hagen-Poiseuille's equation for average velocity in pipes, the Darcy-Weisbach and Moody diagram equations for head loss, major losses due to friction, and minor losses due to elements like bends, fittings, and obstructions. It also discusses boundary layer concepts including laminar and turbulent boundary layers, and defines boundary layer thickness.Quasi steady and unsteady flow
Quasi steady and unsteady flowGhulam Murtaza
?
This document defines and describes different types of fluid flows. It discusses ideal and real fluids, Newtonian and non-Newtonian fluids, laminar and turbulent flow, steady and unsteady flow, uniform and non-uniform flow, compressible and incompressible flow, rotational and irrotational flow, and viscous and non-viscous flow. Key fluid properties like viscosity, density, and compressibility are covered. Examples are provided to illustrate different fluid types and flows.Boundary layer theory 2
Boundary layer theory 2sistec
?
This document summarizes key concepts and formulas related to boundary layer theory, including displacement thickness, momentum thickness, energy thickness, and shape factor. It provides an example problem calculating these values for a given boundary layer velocity distribution. The next lecture topic is introduced as the momentum integral equation.Fluid Mechanics - Fluid Dynamics
Fluid Mechanics - Fluid DynamicsMalla Reddy University
?
The document outlines a syllabus for a fluid dynamics course, covering topics such as fluid statics, kinematics, dynamics, and boundary layer theory. Key concepts include the calculation of pressure, flow rates using various devices, and applications of Bernoulli's equation. The course aims to provide a comprehensive understanding of fluid behavior and the forces acting on fluids.Fluid Mechanics - Fluid Pressure and its measurement
Fluid Mechanics - Fluid Pressure and its measurementMalla Reddy University
?
This document provides an overview of fluid pressure and measurement techniques. It begins with defining key concepts like hydrostatic pressure, Pascal's law, and pressure variation in static fluids. It then describes various devices used to measure pressure, including manometers (U-tube, single column, differential), and mechanical gauges (diaphragm, Bourdon tube, dead-weight, bellows). The document is divided into 5 units covering fluid statics, kinematics, dynamics, pipe flow, and dimensional analysis with the goal of teaching students to calculate pressure, hydrostatic forces, fluid flow, and losses in closed conduits.Flow through pipes ppt
Flow through pipes pptVishal Chaudhari
?
This document discusses laminar and turbulent fluid flow in pipes. It defines the Reynolds number and explains that laminar flow occurs at Re < 2000, transitional flow from 2000 to 4000, and turbulent flow over 4000. The entrance length for developing pipe flow profiles is discussed. Fully developed laminar and turbulent pipe flows are compared. Equations are provided for average velocity, shear stress at the wall, and pressure drop based on conservation of momentum and energy analyses. The Darcy friction factor is defined, and methods for calculating it for laminar and turbulent flows are explained, including the Moody chart. Types of pipe flow problems and accounting for minor losses and pipe networks are also summarized.Boundary layer
Boundary layerVishal Chaudhari
?
The document outlines boundary layer theory, covering the concepts of laminar and turbulent boundary layers, displacement thickness, and methods to control boundary layer separation, first introduced by L. Prandtl in 1904. It explains the gradual increase in fluid velocity within a boundary layer over a flat plate and discusses the implications of pressure gradients on boundary layer behavior. Additionally, it presents various methods to prevent separation, such as fluid injection and suction techniques.Open Channel VS Pipe Flow
Open Channel VS Pipe FlowFatma Abdalla
?
Pipe flow involves fluid completely filling a pipe, while open channel flow has a free surface. In pipe flow, pressure varies along the pipe but remains constant at the free surface in open channels. The main driving force is gravity in open channels and pressure gradient in pipes. Flow properties like cross-sectional area and velocity profile differ between the two flow types.Terbulent Flow in fluid mechanics
Terbulent Flow in fluid mechanicsPavan Narkhede
?
This document provides an overview of turbulent fluid flow, including:
1) Turbulent flow occurs when the Reynolds number is greater than 2000 and involves irregular, random movement of fluid particles in all directions.
2) The magnitude and intensity of turbulence can be calculated based on the root mean square of turbulent fluctuations and the average flow velocity.
3) The Moody diagram relates the friction factor to the Reynolds number and relative roughness of a pipe to characterize head losses in turbulent pipe flow.UNIT 1 UNIFORM FLOW.pptx
UNIT 1 UNIFORM FLOW.pptxreenarana28
?
The document discusses the principles and characteristics of open channel flow, covering topics such as types of channels, flow classification, velocity and pressure distribution, and the concept of uniform and non-uniform flow. It details the geometric elements of open channels, including prismatic and non-prismatic channels, and provides empirical formulas like the Chezy and Manning equations to calculate discharge. Additionally, it emphasizes the importance of minimizing the wetted perimeter for cost-effective channel design.Separation of boundary layer
Separation of boundary layerKaran Patel
?
The document discusses boundary layer separation in fluid mechanics, detailing how flow over a solid surface results in an increasing boundary layer thickness and changing velocity profiles. It explains the influence of pressure gradients on boundary layer behavior and identifies points of separation where fluid flow detaches from surfaces, causing resistance and disturbed fluid zones. Additionally, it outlines methods for controlling boundary layer separation, such as fluid acceleration, suction, guide vanes, and adjustments in geometry like diffuser angles.Fluid Kinematics
Fluid KinematicsMalla Reddy University
?
This document provides an overview of fluid kinematics, which is the study of fluid motion without considering forces. It discusses key concepts like streamlines, pathlines, and streaklines. It describes Lagrangian and Eulerian methods for describing fluid motion. It also covers various types of fluid flow such as steady/unsteady, laminar/turbulent, compressible/incompressible, and one/two/three-dimensional flow. Important topics like continuity equation, velocity, acceleration, and stream/velocity potential functions are also summarized. The document is intended to outline the syllabus and learning objectives for a course unit on fluid kinematics.Fluid kinematics
Fluid kinematicsMohsin Siddique
?
This document discusses key concepts in fluid dynamics, including:
(i) Fluid kinematics describes fluid motion without forces/energies, examining geometry of motion through concepts like streamlines and pathlines.
(ii) Fluids can flow steadily or unsteadily, uniformly or non-uniformly, laminarly or turbulently depending on properties of the flow and fluid.
(iii) The continuity equation states that mass flow rate remains constant for an incompressible, steady flow through a control volume according to the principle of conservation of mass.Fluid Mechanics
Fluid MechanicsDhrumit Patel
?
The document outlines fundamental concepts in fluid mechanics, focusing on pressure definitions, Pascal's law, and hydrostatic principles. It describes various types of pressure, including gauge, vacuum, and absolute pressure, and details measurement devices such as manometers, including piezometers and u-tube manometers. Limitations and applications of each measurement type are discussed, emphasizing their relevance in engineering and fluid technology.Boundary layer equation
Boundary layer equationJustin Myint
?
1) The document discusses different definitions of boundary layer thickness, including nominal thickness, displacement thickness, momentum thickness, and energy thickness. Equations are provided for calculating each type of thickness.
2) Key assumptions of boundary layer theory are that the boundary layer is thin compared to the body and flow is two-dimensional and steady. The Prandtl boundary layer equations are derived using control volume analysis and assumptions of constant density and viscosity.
3) The Prandtl boundary layer equation equates forces within the boundary layer, including pressure and shear stress, to the net rate of momentum change and forms the basis for boundary layer analysis.Unit i- properties of fluid
Unit i- properties of fluidsubhash kumar
?
The document covers the principles and properties of fluid mechanics, including fluid statics, kinematics, and dynamics, along with the distinction between solids and fluids. It details various categories of fluid mechanics, such as hydrodynamics and aerodynamics, and introduces essential properties of fluids, including density, specific weight, viscosity, and specific gravity. The content includes definitions, mathematical relationships, and practical applications, showcasing the behavior of fluids in both static and dynamic states.Tarbulent flow
Tarbulent flowMeet612
?
This document discusses turbulent fluid flow. It defines turbulence as an irregular flow with random variations in time and space that can be expressed statistically. Turbulence occurs above a critical Reynolds number when the kinetic energy of the flow is enough to sustain random fluctuations against viscous damping. Characteristics of turbulent flow include fluctuating velocities and pressures, and more uniform velocity distributions compared to laminar flow. Turbulence can be generated by solid walls or shear between layers, and can be categorized as homogeneous, isotropic, or anisotropic. Transition from laminar to turbulent flow is also discussed.Open Channel Flow
Open Channel FlowParth Desani
?
This document discusses open channel flow. It defines open channel flow and describes the different types of channels and flows that can occur, including steady/unsteady, uniform/non-uniform, laminar/turbulent, sub-critical/super-critical flows. It also discusses point velocity, how velocity varies across a channel, and how the average velocity is calculated.Flow In Pipes
Flow In PipesIla Lee
?
This document discusses laminar and turbulent flow in pipes. It defines the critical Reynolds number that distinguishes between the two flow regimes. For non-circular pipes, it introduces the hydraulic diameter to characterize the pipe geometry. The document then covers topics such as the developing flow region, fully developed flow profiles and pressure drop, the friction factor, minor losses, pipe networks, and pump selection.Fluid MechanicsLosses in pipes dynamics of viscous flows
Fluid MechanicsLosses in pipes dynamics of viscous flowsMohsin Siddique
?
This document discusses fluid flow in pipes. It defines the Reynolds number and explains laminar and turbulent flow regimes. It also covers the Darcy-Weisbach equation for calculating head losses due to pipe friction. The friction factor is determined using Moody diagrams based on Reynolds number and relative pipe roughness. Examples are provided to calculate friction factor, head loss, and flow rate for different pipe flow conditions.Losses in Pipe
Losses in PipeVikramsinh Tiware
?
Unit 6 discusses losses in pipes, including major and minor losses. Major losses are due to friction and calculated using Darcy-Weisbach or Chezy's formulas. Minor losses are due to changes in pipe direction, size, or obstructions and are also calculated using specific formulas. The document also discusses equivalent pipes, pipes in series, pipes in parallel, and two and three reservoir pipe flow analysis problems. Head losses are calculated using friction and minor loss formulas, and continuity and energy equations are used to analyze pipe flows.Deep Learning for Natural Language Processing_FDP on 16 June 2025 MITS.pptx
Deep Learning for Natural Language Processing_FDP on 16 June 2025 MITS.pptxresming1
?
This gives an introduction to how NLP has evolved from the time of World War II till this date through the advances in approaches, architectures and word representations. From rule based approaches, it advanced to statistical approaches. from traditional machine learning algorithms it advanced to deep neural network architectures. Deep neural architectures include recurrent neural networks, long short term memory, gated recurrent units, seq2seq models, encoder decoder models, transformer architecture, upto large language models and vision language models which are multimodal in nature.4th International Conference on Computer Science and Information Technology (...
4th International Conference on Computer Science and Information Technology (...ijait
?
4th International Conference on Computer Science and Information Technology
(COMSCI 2025) will act as a major forum for the presentation of innovative ideas,
approaches, developments, and research projects in the area computer Science and
Information Technology. It will also serve to facilitate the exchange of information
between researchers and industry professionals to discuss the latest issues and
advancement in the research area.More Related Content
What's hot (20)
Quasi steady and unsteady flow
Quasi steady and unsteady flowGhulam Murtaza
?
This document defines and describes different types of fluid flows. It discusses ideal and real fluids, Newtonian and non-Newtonian fluids, laminar and turbulent flow, steady and unsteady flow, uniform and non-uniform flow, compressible and incompressible flow, rotational and irrotational flow, and viscous and non-viscous flow. Key fluid properties like viscosity, density, and compressibility are covered. Examples are provided to illustrate different fluid types and flows.Boundary layer theory 2
Boundary layer theory 2sistec
?
This document summarizes key concepts and formulas related to boundary layer theory, including displacement thickness, momentum thickness, energy thickness, and shape factor. It provides an example problem calculating these values for a given boundary layer velocity distribution. The next lecture topic is introduced as the momentum integral equation.Fluid Mechanics - Fluid Dynamics
Fluid Mechanics - Fluid DynamicsMalla Reddy University
?
The document outlines a syllabus for a fluid dynamics course, covering topics such as fluid statics, kinematics, dynamics, and boundary layer theory. Key concepts include the calculation of pressure, flow rates using various devices, and applications of Bernoulli's equation. The course aims to provide a comprehensive understanding of fluid behavior and the forces acting on fluids.Fluid Mechanics - Fluid Pressure and its measurement
Fluid Mechanics - Fluid Pressure and its measurementMalla Reddy University
?
This document provides an overview of fluid pressure and measurement techniques. It begins with defining key concepts like hydrostatic pressure, Pascal's law, and pressure variation in static fluids. It then describes various devices used to measure pressure, including manometers (U-tube, single column, differential), and mechanical gauges (diaphragm, Bourdon tube, dead-weight, bellows). The document is divided into 5 units covering fluid statics, kinematics, dynamics, pipe flow, and dimensional analysis with the goal of teaching students to calculate pressure, hydrostatic forces, fluid flow, and losses in closed conduits.Flow through pipes ppt
Flow through pipes pptVishal Chaudhari
?
This document discusses laminar and turbulent fluid flow in pipes. It defines the Reynolds number and explains that laminar flow occurs at Re < 2000, transitional flow from 2000 to 4000, and turbulent flow over 4000. The entrance length for developing pipe flow profiles is discussed. Fully developed laminar and turbulent pipe flows are compared. Equations are provided for average velocity, shear stress at the wall, and pressure drop based on conservation of momentum and energy analyses. The Darcy friction factor is defined, and methods for calculating it for laminar and turbulent flows are explained, including the Moody chart. Types of pipe flow problems and accounting for minor losses and pipe networks are also summarized.Boundary layer
Boundary layerVishal Chaudhari
?
The document outlines boundary layer theory, covering the concepts of laminar and turbulent boundary layers, displacement thickness, and methods to control boundary layer separation, first introduced by L. Prandtl in 1904. It explains the gradual increase in fluid velocity within a boundary layer over a flat plate and discusses the implications of pressure gradients on boundary layer behavior. Additionally, it presents various methods to prevent separation, such as fluid injection and suction techniques.Open Channel VS Pipe Flow
Open Channel VS Pipe FlowFatma Abdalla
?
Pipe flow involves fluid completely filling a pipe, while open channel flow has a free surface. In pipe flow, pressure varies along the pipe but remains constant at the free surface in open channels. The main driving force is gravity in open channels and pressure gradient in pipes. Flow properties like cross-sectional area and velocity profile differ between the two flow types.Terbulent Flow in fluid mechanics
Terbulent Flow in fluid mechanicsPavan Narkhede
?
This document provides an overview of turbulent fluid flow, including:
1) Turbulent flow occurs when the Reynolds number is greater than 2000 and involves irregular, random movement of fluid particles in all directions.
2) The magnitude and intensity of turbulence can be calculated based on the root mean square of turbulent fluctuations and the average flow velocity.
3) The Moody diagram relates the friction factor to the Reynolds number and relative roughness of a pipe to characterize head losses in turbulent pipe flow.UNIT 1 UNIFORM FLOW.pptx
UNIT 1 UNIFORM FLOW.pptxreenarana28
?
The document discusses the principles and characteristics of open channel flow, covering topics such as types of channels, flow classification, velocity and pressure distribution, and the concept of uniform and non-uniform flow. It details the geometric elements of open channels, including prismatic and non-prismatic channels, and provides empirical formulas like the Chezy and Manning equations to calculate discharge. Additionally, it emphasizes the importance of minimizing the wetted perimeter for cost-effective channel design.Separation of boundary layer
Separation of boundary layerKaran Patel
?
The document discusses boundary layer separation in fluid mechanics, detailing how flow over a solid surface results in an increasing boundary layer thickness and changing velocity profiles. It explains the influence of pressure gradients on boundary layer behavior and identifies points of separation where fluid flow detaches from surfaces, causing resistance and disturbed fluid zones. Additionally, it outlines methods for controlling boundary layer separation, such as fluid acceleration, suction, guide vanes, and adjustments in geometry like diffuser angles.Fluid Kinematics
Fluid KinematicsMalla Reddy University
?
This document provides an overview of fluid kinematics, which is the study of fluid motion without considering forces. It discusses key concepts like streamlines, pathlines, and streaklines. It describes Lagrangian and Eulerian methods for describing fluid motion. It also covers various types of fluid flow such as steady/unsteady, laminar/turbulent, compressible/incompressible, and one/two/three-dimensional flow. Important topics like continuity equation, velocity, acceleration, and stream/velocity potential functions are also summarized. The document is intended to outline the syllabus and learning objectives for a course unit on fluid kinematics.Fluid kinematics
Fluid kinematicsMohsin Siddique
?
This document discusses key concepts in fluid dynamics, including:
(i) Fluid kinematics describes fluid motion without forces/energies, examining geometry of motion through concepts like streamlines and pathlines.
(ii) Fluids can flow steadily or unsteadily, uniformly or non-uniformly, laminarly or turbulently depending on properties of the flow and fluid.
(iii) The continuity equation states that mass flow rate remains constant for an incompressible, steady flow through a control volume according to the principle of conservation of mass.Fluid Mechanics
Fluid MechanicsDhrumit Patel
?
The document outlines fundamental concepts in fluid mechanics, focusing on pressure definitions, Pascal's law, and hydrostatic principles. It describes various types of pressure, including gauge, vacuum, and absolute pressure, and details measurement devices such as manometers, including piezometers and u-tube manometers. Limitations and applications of each measurement type are discussed, emphasizing their relevance in engineering and fluid technology.Boundary layer equation
Boundary layer equationJustin Myint
?
1) The document discusses different definitions of boundary layer thickness, including nominal thickness, displacement thickness, momentum thickness, and energy thickness. Equations are provided for calculating each type of thickness.
2) Key assumptions of boundary layer theory are that the boundary layer is thin compared to the body and flow is two-dimensional and steady. The Prandtl boundary layer equations are derived using control volume analysis and assumptions of constant density and viscosity.
3) The Prandtl boundary layer equation equates forces within the boundary layer, including pressure and shear stress, to the net rate of momentum change and forms the basis for boundary layer analysis.Unit i- properties of fluid
Unit i- properties of fluidsubhash kumar
?
The document covers the principles and properties of fluid mechanics, including fluid statics, kinematics, and dynamics, along with the distinction between solids and fluids. It details various categories of fluid mechanics, such as hydrodynamics and aerodynamics, and introduces essential properties of fluids, including density, specific weight, viscosity, and specific gravity. The content includes definitions, mathematical relationships, and practical applications, showcasing the behavior of fluids in both static and dynamic states.Tarbulent flow
Tarbulent flowMeet612
?
This document discusses turbulent fluid flow. It defines turbulence as an irregular flow with random variations in time and space that can be expressed statistically. Turbulence occurs above a critical Reynolds number when the kinetic energy of the flow is enough to sustain random fluctuations against viscous damping. Characteristics of turbulent flow include fluctuating velocities and pressures, and more uniform velocity distributions compared to laminar flow. Turbulence can be generated by solid walls or shear between layers, and can be categorized as homogeneous, isotropic, or anisotropic. Transition from laminar to turbulent flow is also discussed.Open Channel Flow
Open Channel FlowParth Desani
?
This document discusses open channel flow. It defines open channel flow and describes the different types of channels and flows that can occur, including steady/unsteady, uniform/non-uniform, laminar/turbulent, sub-critical/super-critical flows. It also discusses point velocity, how velocity varies across a channel, and how the average velocity is calculated.Flow In Pipes
Flow In PipesIla Lee
?
This document discusses laminar and turbulent flow in pipes. It defines the critical Reynolds number that distinguishes between the two flow regimes. For non-circular pipes, it introduces the hydraulic diameter to characterize the pipe geometry. The document then covers topics such as the developing flow region, fully developed flow profiles and pressure drop, the friction factor, minor losses, pipe networks, and pump selection.Fluid MechanicsLosses in pipes dynamics of viscous flows
Fluid MechanicsLosses in pipes dynamics of viscous flowsMohsin Siddique
?
This document discusses fluid flow in pipes. It defines the Reynolds number and explains laminar and turbulent flow regimes. It also covers the Darcy-Weisbach equation for calculating head losses due to pipe friction. The friction factor is determined using Moody diagrams based on Reynolds number and relative pipe roughness. Examples are provided to calculate friction factor, head loss, and flow rate for different pipe flow conditions.Losses in Pipe
Losses in PipeVikramsinh Tiware
?
Unit 6 discusses losses in pipes, including major and minor losses. Major losses are due to friction and calculated using Darcy-Weisbach or Chezy's formulas. Minor losses are due to changes in pipe direction, size, or obstructions and are also calculated using specific formulas. The document also discusses equivalent pipes, pipes in series, pipes in parallel, and two and three reservoir pipe flow analysis problems. Head losses are calculated using friction and minor loss formulas, and continuity and energy equations are used to analyze pipe flows.Recently uploaded (20)
Deep Learning for Natural Language Processing_FDP on 16 June 2025 MITS.pptx
Deep Learning for Natural Language Processing_FDP on 16 June 2025 MITS.pptxresming1
?
This gives an introduction to how NLP has evolved from the time of World War II till this date through the advances in approaches, architectures and word representations. From rule based approaches, it advanced to statistical approaches. from traditional machine learning algorithms it advanced to deep neural network architectures. Deep neural architectures include recurrent neural networks, long short term memory, gated recurrent units, seq2seq models, encoder decoder models, transformer architecture, upto large language models and vision language models which are multimodal in nature.4th International Conference on Computer Science and Information Technology (...
4th International Conference on Computer Science and Information Technology (...ijait
?
4th International Conference on Computer Science and Information Technology
(COMSCI 2025) will act as a major forum for the presentation of innovative ideas,
approaches, developments, and research projects in the area computer Science and
Information Technology. It will also serve to facilitate the exchange of information
between researchers and industry professionals to discuss the latest issues and
advancement in the research area.NALCO Green Anode Plant,Compositions of CPC,Pitch
NALCO Green Anode Plant,Compositions of CPC,Pitcharpitprachi123
?
Its a pdf about all the process involving in the green anode production3. What is the principles of Teamwork_Module_V1.0.ppt
3. What is the principles of Teamwork_Module_V1.0.pptengaash9
?
Demonstrate the role of teamwork in the execution of systems engineering.
Describe the principles of successful teams.
ÉçÄÚĂ㏊»áŮYÁĎ_Chain of Thought .
ÉçÄÚĂ㏊»áŮYÁĎ_Chain of Thought .±·´ˇµţł˘´ˇł§ÖęĘ˝»áÉç
?
±ľŮYÁϡ¸To CoT or not to CoT?ˇą¤Ç¤Ďˇ˘´óŇŽÄŁŃÔŐZĄâĄÇĄë¤Ë¤Ş¤±¤ëChain of ThoughtŁ¨CoTŁ©Ą×ĄíĄóĄ×ĄČ¤Î„żąű¤Ë¤Ä¤¤¤ĆÔ”¤·¤Ż˝âŐh¤·¤Ć¤¤¤Ţ¤ąˇŁ
CoT¤Ď¤˘¤é¤ć¤ëĄżĄąĄŻ¤Ë„ż¤ŻÍňÄܤĘĘÖ·¨¤Ç¤Ď¤Ę¤Żˇ˘ĚؤËĘýѧµÄ?Ő“ŔíµÄ?Ą˘ĄëĄ´ĄęĄşĄŕµÄ¤ĘÍĆŐ“¤ň°é¤¦Őnî}¤Ç¸ß¤¤„żąű¤ň°k“]¤ą¤ë¤ł¤Č¤¬ŚgňY¤«¤éĘľ¤µ¤ě¤Ć¤¤¤Ţ¤ąˇŁ
Ň»·˝¤Çˇ˘łŁ×R¤äŇ»°ăÖŞ×R¤ň†–¤¦†–î}¤ËŚť¤·¤Ć¤Ď„żąű¤¬Ď޶¨µÄ¤Ç¤˘¤ë¤ł¤Č¤âĂ÷¤é¤«¤Ë¤Ę¤ę¤Ţ¤·¤żˇŁ
Ń}ëj¤Ę†–î}¤ň¶ÎëAµÄ¤Ë·Ö˝â?ŚgĐФą¤ëˇ¸Ó‹»¤ČŚgĐСą¤ÎĄ×ĄíĄ»Ąą¤Ë¤Ş¤¤¤Ćˇ˘CoT¤ÎŹŠ¤ß¤¬»î¤«¤µ¤ě¤ëµă¤âעĿĄÝĄ¤ĄóĄČ¤Ç¤ąˇŁ
This presentation explores when Chain of Thought (CoT) prompting is truly effective in large language models.
The findings show that CoT significantly improves performance on tasks involving mathematical or logical reasoning, while its impact is limited on general knowledge or commonsense tasks.Cadastral Maps
Cadastral MapsGoogle
?
Preparation of cadastral maps based by Engineer Dungo Tizazu from Dire Dawa University Water demand - Types , variations and WDS
Water demand - Types , variations and WDSdhanashree78
?
Water demand refers to the volume of water needed or requested by users for various purposes. It encompasses the water required for domestic, industrial, agricultural, public, and other uses. Essentially, it represents the overall need or quantity of water required to meet the demands of different sectors and activities. Impurities of Water and their Significance.pptx
Impurities of Water and their Significance.pptxdhanashree78
?
Impart Taste, Odour, Colour, and Turbidity to water.
Presence of organic matter or industrial wastes or microorganisms (algae) imparts taste and odour to water.
Presence of suspended and colloidal matter imparts turbidity to water.
How Binning Affects LED Performance & Consistency.pdf
How Binning Affects LED Performance & Consistency.pdfMina Anis
?
? WhatˇŻs Inside:
? What Is LED Binning?
? The process of sorting LEDs by color temperature, brightness, voltage, and CRI
? Ensures visual and performance consistency across large installations
? Why It Matters:
? Inconsistent binning leads to uneven color and brightness
? Impacts brand perception, customer satisfaction, and warranty claims
? Key Concepts Explained:
? SDCM (Standard Deviation of Color Matching)
? Recommended bin tolerances by application (e.g., 1¨C3 SDCM for retail/museums)
? How to read bin codes from LED datasheets
? The difference between ANSI/NEMA standards and proprietary bin maps
? Advanced Practices:
? AI-assisted bin prediction
? Color blending and dynamic calibration
? Customized binning for high-end or global projectsVARICELLA VACCINATION: A POTENTIAL STRATEGY FOR PREVENTING MULTIPLE SCLEROSIS
VARICELLA VACCINATION: A POTENTIAL STRATEGY FOR PREVENTING MULTIPLE SCLEROSISijab2
?
Multiple sclerosis (MS) is a debilitating neurological condition affecting approximately 2.9 million people worldwide. Its cause remains unclear but environmental factors, such as post-childhood Epstein-Barr virus (EBV) infection, are thought to contribute to MS incidence. Machine Learning - Classification Algorithms
Machine Learning - Classification Algorithmsresming1
?
This covers traditional machine learning algorithms for classification. It includes Support vector machines, decision trees, Naive Bayes classifier , neural networks, etc.
It also discusses about model evaluation and selection. It discusses ID3 and C4.5 algorithms. It also describes k-nearest neighbor classifer.02 - Ethics & Professionalism - BEM, IEM, MySET.PPT
02 - Ethics & Professionalism - BEM, IEM, MySET.PPTSharinAbGhani1
?
ethics & professionalism based on BEMPavement and its types, Application of rigid and Flexible Pavements
Pavement and its types, Application of rigid and Flexible PavementsSakthivel M
?
Pavement and its types, Application of rigid and Flexible PavementsAd
Boundary layer theory 3
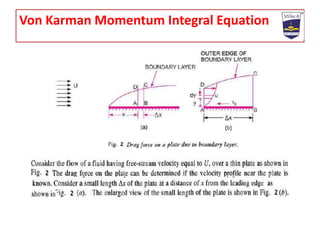
- 1. FLUID MECHANICS BOUNDARY LAYER THEORY LECTURE-03 CONTENTS:- ? Momentum Integral Equation (Von Karman Momentum Integral Equation) PROF. SANJEEV GUPTA
- 2. Von Karman Momentum Integral Equation
- 3. According to the continuity equation for a steady incompressible fluid flow Mass rate of flow entering AD + Mass rate of flow entering DC = Mass Rate of flow leaving BC Mass rate of flow entering DC = Mass Rate of flow leaving BC - Mass rate of flow entering AD Or
- 5. Now let us calculate momentum flux through CV
- 6. Rate of change of momentum of the CV = Momentum flux through BC - Momentum flux through AD - Momentum flux through DC
- 11. THANK YOU!! STAY AT HOME BE SAFE
