BryÅy PlatoÅskie
- 1. Anna WoÅoszyn BryÅy PlatoÅskie "Kto nie zna geometrii, niech do tej szkoÅy nie wstÄpuje" Platon
- 2. âĒ Platon - grecki filozof i uczony ÅžyÅ w latach 427 p. n. e. - 347 p. n. e., wÅaÅciwie nazywaÅ siÄ Arystokles. ImiÄ Platon otrzymaÅ w gimnazjonie ze wzglÄdu na silne plecy (Platon bowiem to tyle co szerokoplecy). âĒ ByÅ uczniem Sokratesa i nauczycielem Arystotelesa. ZaÅoÅžyÅ w Atenach szkoÅÄ zwanÄ AkademiÄ PlatoÅskÄ . Kim byÅ PLATON i dlaczego w matematyce nazwy niektÃģrych pojÄÄ nawiÄ zujÄ do jego osoby? W kosmologii Platona waÅžne miejsce zajmuje teoria piÄciu wieloÅcianÃģw foremnych. Platon zajmowaÅ siÄ rÃģwnieÅž konstrukcjami geometrycznymi, ktÃģre moÅžna wykonywaÄ uÅžywajÄ c tylko cyrkla i liniaÅu. NoszÄ one nazwÄ konstrukcji klasycznych, konstrukcji platoÅskich
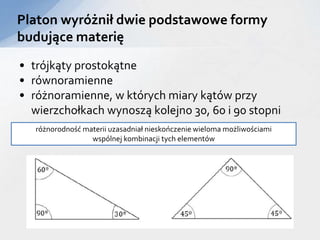
- 3. Platon wyrÃģÅžniÅ dwie podstawowe formy budujÄ ce materiÄ âĒ trÃģjkÄ ty prostokÄ tne âĒ rÃģwnoramienne âĒ rÃģÅžnoramienne, w ktÃģrych miary kÄ tÃģw przy wierzchoÅkach wynoszÄ kolejno 30, 60 i 90 stopni rÃģÅžnorodnoÅÄ materii uzasadniaÅ nieskoÅczenie wieloma moÅžliwoÅciami wspÃģlnej kombinacji tych elementÃģw
- 4. Podstawowe formy Platona Ze zÅoÅženia odpowiedniej iloÅci trÃģjkÄ tÃģw prostokÄ tnych jednego rodzaju, Platon stworzyÅ ukÅad nazwany przez siebie âelementem matematycznymâ. Elementy matematyczne Platona zbudowane z trÃģjkÄ tÃģw prostokÄ tnych rÃģÅžnoramiennych (A) oraz z trÃģjkÄ tÃģw prostokÄ tnych rÃģwnoramiennych (B)
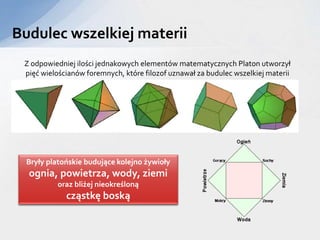
- 5. Budulec wszelkiej materii Z odpowiedniej iloÅci jednakowych elementÃģw matematycznych Platon utworzyÅ piÄÄ wieloÅcianÃģw foremnych, ktÃģre filozof uznawaÅ za budulec wszelkiej materii BryÅy platoÅskie budujÄ ce kolejno ÅžywioÅy ognia, powietrza, wody, ziemi oraz bliÅžej nieokreÅlonÄ czÄ stkÄ boskÄ
- 6. WszechÅwiat tworzÄ cztery elementy: ziemia, powietrze, woda, ogieÅ Platon uznaÅ, Åže atomy muszÄ mieÄ ksztaÅt najpiÄkniejszych bryÅ, a wiÄc wieloÅcianÃģw foremnych. PoniewaÅž bryÅ takich jest piÄÄ, filozof wymyÅliÅ piÄ ty skÅadnik materii: eter, z ktÃģrego zbudowane sÄ ciaÅa niebieskie. MyÅliciele od zawsze zastanawiali siÄ, co jest tam gdzie nic nie ma. DÅugo panujÄ cÄ koncepcjÄ na ten temat byÅa koncepcja eteru wypeÅniajÄ cego caÅy wszechÅwiat. Jednak naukowcy w XIX wieku zanegowali tÄ teoriÄ jako bezzasadnÄ i niemieszczÄ ca siÄ w materialistycznym pojÄciu Åwiata. Przyroda powstaje z bezkresu. Ale jak? Na zasadzie wyÅaniania siÄ przeciwieÅstw. Co powoduje ten proces? Powoduje go wieczny ruch ("WielkiWybuch"); Eter = piÄ ty ÅžywioÅ.
- 7. âĒ BryÅa jest to ograniczona czÄÅÄ przestrzeni. âĒ WieloÅcian jest to bryÅa ograniczona ze wszystkich stron pÅaszczyznami. Jego wszystkie Åciany sÄ wielokÄ tami. âĒ WielokÄ t foremny jest to wielokÄ t, ktÃģry ma wszystkie boki rÃģwne oraz wszystkie kÄ ty rÃģwne. âĒ WieloÅcian foremny to wieloÅcian, ktÃģrego Åcianami sÄ wielokÄ ty foremne. Czym sÄ wieloÅciany foremne? Pitagorejczycy, a pÃģÅšniej sam Platon, uwaÅžali, Åže cztery gÅÃģwne ÅžywioÅy, ktÃģre tworzÄ Åwiat zbudowane sÄ z wieloÅcianÃģw foremnych
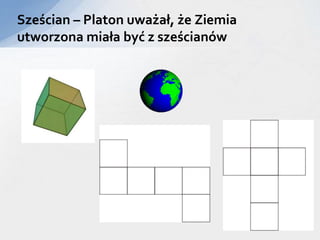
- 8. SzeÅcian â Platon uwaÅžaÅ, Åže Ziemia utworzona miaÅa byÄ z szeÅcianÃģw
- 9. Siatki szeÅcianÃģw â max 11
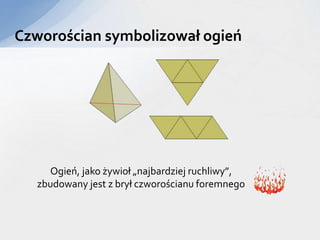
- 10. CzworoÅcian symbolizowaÅ ogieÅ OgieÅ, jako ÅžywioÅ ânajbardziej ruchliwyâ, zbudowany jest z bryÅ czworoÅcianu foremnego
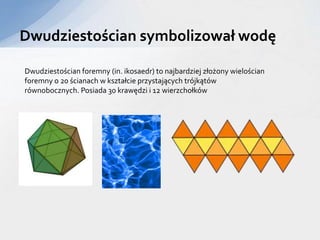
- 12. DwudziestoÅcian symbolizowaÅ wodÄ DwudziestoÅcian foremny (in. ikosaedr) to najbardziej zÅoÅžony wieloÅcian foremny o 20 Åcianach w ksztaÅcie przystajÄ cych trÃģjkÄ tÃģw rÃģwnobocznych. Posiada 30 krawÄdzi i 12 wierzchoÅkÃģw
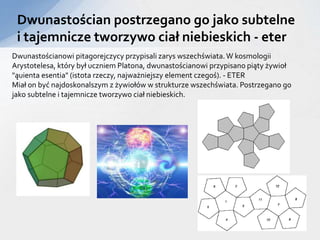
- 13. DwunastoÅcian postrzegano go jako subtelne i tajemnicze tworzywo ciaÅ niebieskich - eter DwunastoÅcianowi pitagorejczycy przypisali zarys wszechÅwiata.W kosmologii Arystotelesa, ktÃģry byÅ uczniem Platona, dwunastoÅcianowi przypisano piÄ ty ÅžywioÅ "Ä uienta esentia" (istota rzeczy, najwaÅžniejszy element czegoÅ). - ETER MiaÅ on byÄ najdoskonalszym z ÅžywioÅÃģw w strukturze wszechÅwiata. Postrzegano go jako subtelne i tajemnicze tworzywo ciaÅ niebieskich.
- 14. Elementy wieloÅcianÃģw foremnych tabela do uzupeÅnienia Nazwa Liczba Åcian i ich ksztaÅt Liczba krawÄdzi Liczba wierzchoÅkÃģw czworoÅcian szeÅcian oÅmioÅcian dwunastoÅcian dwudziestoÅcian
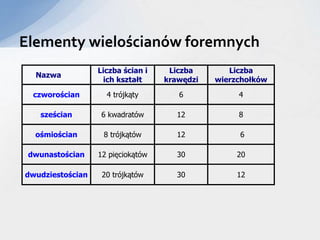
- 15. Elementy wieloÅcianÃģw foremnych Nazwa Liczba Åcian i ich ksztaÅt Liczba krawÄdzi Liczba wierzchoÅkÃģw czworoÅcian 4 trÃģjkÄ ty 6 4 szeÅcian 6 kwadratÃģw 12 8 oÅmioÅcian 8 trÃģjkÄ tÃģw 12 6 dwunastoÅcian 12 piÄciokÄ tÃģw 30 20 dwudziestoÅcian 20 trÃģjkÄ tÃģw 30 12
- 16. Twierdzeniem Eulera o wieloÅcianach wypukÅych JeÅželi wieloÅcian wypukÅy ma w wierzchoÅkÃģw, k krawÄdzi i s Åcian, to w - k + s = 2 lub w + s = k+2 Szwajcarski banknot 10-frankowy, na czeÅÄ Eulera, najznakomitszego szwajcarskiego matematyka w historii
- 17. Czy wyprowadzana zaleÅžnoÅÄ jest zasadna dla innych bryÅ, niekoniecznie platoÅskich? o przystajÄ cych Åcianach, ktÃģre nie sÄ figurami foremnymi, np. trzydziestoÅcian rombowy WieloÅciany Catalana wielokÄ t ma 30 Åcian, 32 wierzchoÅki i 60 krawÄdzi. ZaleÅžnoÅÄ w + s = k+2 jest poprawna dla wszystkich wielokÄ tÃģw wypukÅych
- 18. Zadanie 2 Dodekaedr to dwunastoÅcian, w ktÃģrym wszystkie Åciany sÄ piÄciokÄ tami foremnymi. O bryle tej moÅžna powiedzieÄ, Åže: ma 30 krawÄdzi i 20 wierzchoÅkÃģw krawÄdzi jest 50% wiÄcej niÅž wierzchoÅkÃģw ma 28 krawÄdzi i 18 wierzchoÅkÃģw suma wierzchoÅkÃģw i Åcian rÃģwna jest sumie krawÄdzi powiÄkszonej o dwa
- 19. Zadanie 3 WieloÅciany Catalana majÄ wszystkie Åciany przystajÄ ce, ktÃģre nie sÄ jednak wielokÄ tami foremnymi. Jednym z takich wieloÅcianÃģw jest szeÅÄdziestoÅcian deltoidowy. BryÅa ta ma: 60 wierzchoÅkÃģw 62 wierzchoÅki 58 wierzchoÅkÃģw 2 razy wiÄcej krawÄdzi niÅž Åcian
- 20. Ciekawostka - BryÅy niemoÅžliwe Rysowanie na pÅaszczyÅšnie figur przestrzennych musi byÄ podporzÄ dkowane pewnym reguÅom, aby obraz przedstawiony byÅ zgodny z rzeczywistoÅciÄ . Nieprzestrzeganie tych reguÅ daje w efekcie powstanie figur niemoÅžliwych.
- 21. BryÅy niemoÅžliwe TrÃģjkÄ t Penroseâa Kwadrat Penroseâa
- 22. Claisebrook Roundabout w poÅudniowej Australii O tym, jak popularna i intrygujÄ ca jest ta figura, moÅže ÅwiadczyÄ fakt, Åže trÃģjkÄ t Penroseâa staÅ siÄ inspiracjÄ dla wielu budowli architektonicznych na naszym kontynencie Fot. 2.10. Prawdziwy model niemoÅžliwego trÃģjkÄ ta.To, co zobaczone, zostaÅo uchwycone fotograficznie Autor fotografi i: Bjorn ChristianTorrissen, bjornfree.com
- 24. Schody Penroseâa. Rysunek przedstawia schody zaÅamane czterokrotnie pod kÄ tem 90 stopni. Nie byÅoby w tym nic dziwnego, gdyby nie to, Åže schody prowadzÄ w gÃģrÄ, a jednak na gÃģrÄ po nich nie moÅžna wejÅÄ â ciÄ gle wraca siÄ do punktu wyjÅciowego. Jest to niemoÅžliwe do wykonania w trzech wymiarach, ale dwuwymiarowy rysunek umoÅžliwia przedstawienie tej paradoksalnej budowli dziÄki zakÅÃģceniu perspektywy.
- 25. Åawka nieszczÄÅliwie zakochanych Dwoje mÅodych ludzi siedzÄ cych na jednej Åawce. ZdawaÅoby siÄ, Åže nic nie jest w stanie przeszkodziÄ im w spotkaniu. A jednak tym utrudnieniem jest Åawka. Åawka? Ale jakim cudem? PrzecieÅž siedzÄ c na Åaweczce, nie mogÄ byÄ juÅž bliÅžej siebie. A jednakâĶ
- 26. Platon, PaÅstwo, KsiÄga 6, 510 DE. âMatematycy kreÅlÄ konkretne figury, na ktÃģrych prowadzÄ swoje argumentacje, ale myÅlÄ nie o tych, co wÅaÅnie kreÅlÄ , ale o tych idealnych, prawdziwych, pomyÅlanych, ktÃģrych Åžaden czÅowiek nie moÅže inaczej zobaczyÄ, jak tylko myÅlÄ â