Coreset+SVM (論文紹介)
- 1. 第7回数理輪講 2012/11/16 16:00- コアセットを用いた SVM学習の高速化 [文献紹介] 情報理工学系研究科 数理言語情報学研究室 M2山田直敬 指導教員: 中川裕志 教授
- 2. 紹介論文 ? Core Vector Machines: Fast SVM Training on Very Large Data Sets – Ivor V. Tsang, James T. Kwok, Pak-Ming Cheung – [JMLR ’05] ? 要旨 – SVMの最適化問題を計算幾何学の問題(MEB)に 帰着 – コアセットを用いたMEBの高速近似解法を流用 – SVMの高速化を実現 2
- 3. Why This Paper? ? SVMは性能が良いものの、遅い ? 高速化のニーズがあり様々な手法が研究 されている ? 紹介論文は、問題を全く別の視点から眺 めることで成功している初期の事例 ? 定式化も面白い ? 機械学習アルゴリズムの高速化は個人的 な研究テーマ 3
- 4. 発表の流れ ? Support Vector Machine (SVM) – カーネルによる高次元化 – SVM は重い。大規模データにスケールしない ? Minimum Enclosing Ball (MEB) – コアセットを用いた高速近似解法 ? Core Vector Machine – SVMをMEBのアルゴリズムで解く ? 実験 – 精度はいい勝負/実行速度が非常に速い ? その後の展開 4
- 5. 目次 ? Support Vector Machine (SVM) 機械学習の話 ? Minimum Enclosing Ball (MEB) ? Core Vector Machine ? 実験 ? その後の展開 5
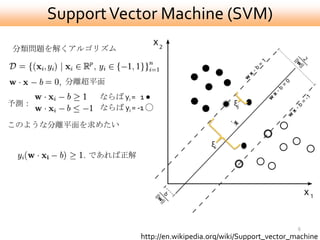
- 6. Support Vector Machine (SVM) 分類問題を解くアルゴリズム 分離超平面 ならば yi = 1 ● 予測: ξj ならば yi = -1 ? このような分離平面を求めたい ξi であれば正解 6 http://en.wikipedia.org/wiki/Support_vector_machine
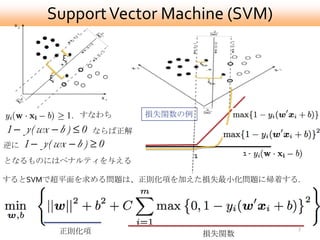
- 7. Support Vector Machine (SVM) ξj ξi すなわち 損失関数の例 ならば正解 逆に 1 1- となるものにはペナルティを与える するとSVMで超平面を求める問題は、正則化項を加えた損失最小化問題に帰着する. 7 正則化項 損失関数
- 8. カーネル法 観察:データが高次元にあれば線形識別器がうまく分類する超平面がありそう ?データを高次元に写像した先で線形SVMを行えば分離性能が良くなる ?一般に分離境界は元の空間に戻って見れば非線形となる. ?カーネルトリックによる巧妙な実現 φ http://stackoverflow.com/questions/1148513/difference-between-a-linear- 8 problem-and-a-non-linear-problem-essence-of-dot-pro
- 9. カーネルトリック(1/2) ?写像 φ : x → φ(x) を施した空間でのSVMの最適化問題 変更はここだけ ?次の双対問題を考える 高次元空間での内積 観察: ?主問題の解 w, bは、双対問題の解 αを用いて復元できる. 高次元での内積さえ あればよい。 φの具体形が要らない ?学習後 新たな入力 x を分類するには, 次を計算すれば良い 9
- 10. カーネルトリック(2/2) ?内積を なるカーネル関数を介して計算すると約束 高次元での内積が 例:ガウシアンカーネル 高速に計算可能に ?すると、双対問題はカーネルを用いて次のように表される ?行列を用いて表すと次の式と等価になる ここで , は要素ごとの積をそれぞれ表す ?カーネルを用いた非線形SVMは α についての(凸)二次計画問題に帰着する 10
- 11. SVMの計算量 ?αについての凸二次計画問題 通常の内点法を用いると各ステップで Kの逆行列が必要となる データ数をm とすると 、Kは m × m の行列 時間計算量 , 空間計算量 激重 激重 ?機械学習ではデータ数 m が大きい場合がほとんど。内点法を用いた最適化は 実用的には使えない。 ?様々な高速化が提案されている Ex. Chunking, SMO , RSVM ,…. 実験的に time 程度 ?紹介論文では 近似アルゴリズムでprovableに time 11
- 12. 目次 ? Support Vector Machine (SVM) ? Minimum Enclosing Ball (MEB) 計算幾何学の話 ? Core Vector Machine ? 実験 ? その後の展開 12
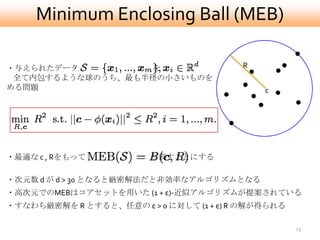
- 13. Minimum Enclosing Ball (MEB) ?与えられたデータ を R 全て内包するような球のうち、最も半径の小さいものを求 める問題 c ?最適な c , Rをもって と表すことにする ?次元数 d が d > 30 となると厳密解法だと非効率なアルゴリズムとなる ?高次元でのMEBはコアセットを用いた (1 + ε)-近似アルゴリズムが提案されている ?すなわち厳密解を R とすると、任意の ε > 0 に対して (1 + ε) R の解が得られる 13
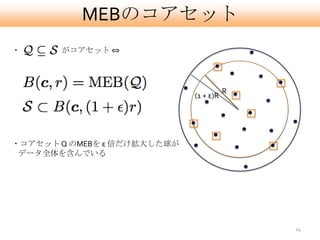
- 14. MEBのコアセット ? がコアセット ? R (1 + ε)R ?コアセット Q のMEBを ε 倍だけ拡大した球が データ全体を含んでいる 14
- 15. MEBコアセットを求めるアルゴリズム() ?B?doiu & Clarkson (2002) [1] ? 反復アルゴリズム ? S, c, R の初期化 – S0 , c0 , R0 – 適当なデータ z ∈ S を とり, S0 = { z } とする – c0 = z – R0 = 0 15
- 16. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 16
- 17. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 17
- 18. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 18
- 19. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 19
- 20. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 20
- 21. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 21
- 22. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 22
- 23. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 23
- 24. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 24
- 25. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) 25
- 26. MEBコアセットを求めるアルゴリズム ?B?doiu & Clarkson (2002) [1] ? 各ステップ tで St , ct , Rt を次のよ うに更新 1. ct から最も遠い点 z を 見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) Rt+1 = RMEB(St+1) ? εR だけ拡大した球が全ての点を 含めば終了 26
- 27. MEBコアセットを求めるアルゴリズム ? アルゴリズムのステップ数は 1/ ε 回 ? コアセットに1個づつ点を追加する ? 途中で小さい問題に対するMEBを厳密に 解いている ? コアセットの要素数は 1/ε 個 27
- 28. 目次 ? Support Vector Machine (SVM) ? Minimum Enclosing Ball (MEB) ? Core Vector Machine 本題 ? 実験 ? その後の展開 28
- 29. Core Vector Machine (CVM) (1/4) ?MEBの双対問題を考える ?行列で書くと ?なお、双対問題の解 α から c, Rは次のように復元できる 29
- 30. Core Vector Machine (CVM) [2/4] (MEBの双対) ?ここでKについて一つだけ仮定をおく ? (定数) ? これはガウシアンカーネル等様々なカーネルで成り立つ ?すると、 となるのでMEBの双対問題は となる。 同じ構造を持ってる! (SVMの双対) 30
- 31. Core Vector Machine (CVM) [3/4] ?逆にSVM側から考えると、 (SVMの双対) において, ,where とすれば を得る ? であることに注意すればSVMは なる空間上でのMEBを解いていることと同じ 31
- 32. Core Vector Machine (CVM) [4/4] ? S0, c0, R0 を初期化 ? 各ステップ tで St , ct , Rt を次のよ うに更新 距離計算は を介して行う 1. ct から最も遠い点 z を見つける 2. St+1 = St ∪ { z } 3. St+1 のMEBを求める 4. ct+1 = cMEB(St+1) 小さいQPを解く必要がある ここは既存のSVMソルバ Rt+1 = RMEB(St+1) (SMO)を用いる ? εR だけ拡大した球が全ての点を 含めば終了 32
- 33. Core Vector Machine の理論保証 ?時間計算量 ?空間計算量 ?データ数について”線形” な時間で最適解に近づく ?近似精度と計算量のトレードオフ ?データ数m が大きければ大きいほど効果が絶大 ?実験ではヒューリスティクスを用いてさらなる高速化を図っている 33
- 34. 目次 ? Support Vector Machine (SVM) ? Minimum Enclosing Ball (MEB) ? Core Vector Machine ? 実験 ? その後の展開 34
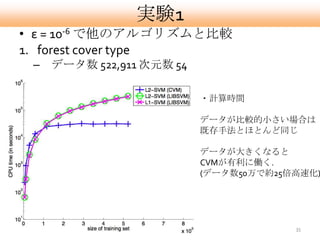
- 35. 実験1 ? ε = 10-6 で他のアルゴリズムと比較 1. forest cover type – データ数 522,911 次元数 54 ?計算時間 データが比較的小さい場合は 既存手法とほとんど同じ データが大きくなると CVMが有利に働く. (データ数50万で約25倍高速化) 35
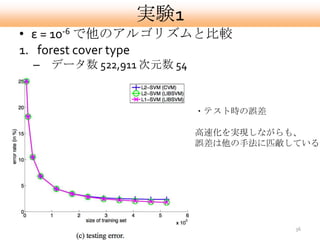
- 36. 実験1 ? ε = 10-6 で他のアルゴリズムと比較 1. forest cover type – データ数 522,911 次元数 54 ?テスト時の誤差 高速化を実現しながらも、 誤差は他の手法に匹敵している 36
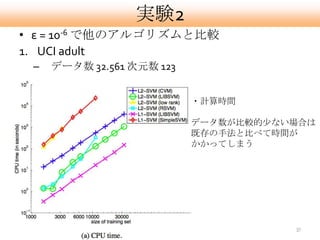
- 37. 実験2 ? ε = 10-6 で他のアルゴリズムと比較 1. UCI adult – データ数 32.561 次元数 123 ?計算時間 データ数が比較的尐ない場合は 既存の手法と比べて時間が かかってしまう 37
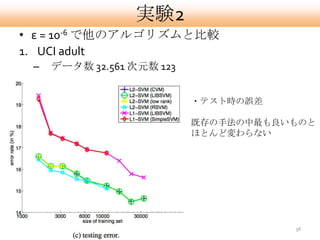
- 38. 実験2 ? ε = 10-6 で他のアルゴリズムと比較 1. UCI adult – データ数 32.561 次元数 123 ?テスト時の誤差 既存の手法の中最も良いものと ほとんど変わらない 38
- 39. Core Vector Machine まとめ ? 機械学習の(L2)SVMと計算幾何学のMEBは 双対問題にすれば同じ構造を持っていた ? コアセットを用いてMEBを効率的に求め る近似アルゴリズムがSVMにも適用でき る ? データ数が多い場合は、精度を保ちつつ、 既存アルゴリズムよりも高速に学習可能 ? データ数が尐ない場合には不向き 39
- 40. CVM その後の展開 ? 回帰問題にも応用 – Core Vector Regression [3] ’05 ? 小さい問題でMEBを解くところを改良 高 速化 – Ball Vector Machine [3] ‘07 ? バッチではなくストリームでCVMを実行 – One Pass SVM [5] ’09 40
- 41. 参考文献 年代順 1. M. B?doiu & K. L. Clarkson. “Optimal core sets for balls”, Computational Geometry, 2002. 2. I. W. Tsang, J. T. Kwok & P. Cheung. “Core Vector Machines: Fast SVM Training on Very Large Data Sets”, JMLR,2005. 3. I. W. Tsang, J. T. Kwok & KT. Lai. “Core Vector Regression for Very Large Regression Problems”, ICML, 2005. 4. I. W. Tsang, A. Kocsor, J. T. Kwok. “Simpler core vector machines with enclosing balls”, ICML, 2007. 5. P. Rai, H. Daum?e III, S. Venkatasubramanian. “Streamed Learning: One-Pass SVMs” , IJCAI , 2009 41

![第7回数理輪講 2012/11/16 16:00-
コアセットを用いた
SVM学習の高速化
[文献紹介]
情報理工学系研究科
数理言語情報学研究室 M2山田直敬
指導教員: 中川裕志 教授](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-1-320.jpg)
![紹介論文
? Core Vector Machines:
Fast SVM Training on Very Large Data Sets
– Ivor V. Tsang, James T. Kwok, Pak-Ming Cheung
– [JMLR ’05]
? 要旨
– SVMの最適化問題を計算幾何学の問題(MEB)に
帰着
– コアセットを用いたMEBの高速近似解法を流用
– SVMの高速化を実現
2](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-2-320.jpg)








![MEBコアセットを求めるアルゴリズム()
?B?doiu & Clarkson (2002) [1]
? 反復アルゴリズム
? S, c, R の初期化
– S0 , c0 , R0
– 適当なデータ z ∈ S を
とり, S0 = { z } とする
– c0 = z
– R0 = 0
15](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-15-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
16](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-16-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
17](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-17-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
18](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-18-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
19](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-19-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
20](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-20-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
21](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-21-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
22](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-22-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
23](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-23-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
24](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-24-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
25](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-25-320.jpg)
![MEBコアセットを求めるアルゴリズム
?B?doiu & Clarkson (2002) [1]
? 各ステップ tで St , ct , Rt を次のよ
うに更新
1. ct から最も遠い点 z を
見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1)
Rt+1 = RMEB(St+1)
? εR だけ拡大した球が全ての点を
含めば終了
26](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-26-320.jpg)



![Core Vector Machine (CVM) [2/4]
(MEBの双対)
?ここでKについて一つだけ仮定をおく
? (定数)
? これはガウシアンカーネル等様々なカーネルで成り立つ
?すると、 となるのでMEBの双対問題は
となる。
同じ構造を持ってる!
(SVMの双対) 30](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-30-320.jpg)
![Core Vector Machine (CVM) [3/4]
?逆にSVM側から考えると、
(SVMの双対)
において,
,where
とすれば を得る
? であることに注意すればSVMは
なる空間上でのMEBを解いていることと同じ
31](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-31-320.jpg)
![Core Vector Machine (CVM) [4/4]
? S0, c0, R0 を初期化
? 各ステップ tで St , ct , Rt を次のよ
うに更新 距離計算は を介して行う
1. ct から最も遠い点 z
を見つける
2. St+1 = St ∪ { z }
3. St+1 のMEBを求める
4. ct+1 = cMEB(St+1) 小さいQPを解く必要がある
ここは既存のSVMソルバ
Rt+1 = RMEB(St+1) (SMO)を用いる
? εR だけ拡大した球が全ての点を
含めば終了
32](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-32-320.jpg)



![CVM その後の展開
? 回帰問題にも応用
– Core Vector Regression [3] ’05
? 小さい問題でMEBを解くところを改良 高
速化
– Ball Vector Machine [3] ‘07
? バッチではなくストリームでCVMを実行
– One Pass SVM [5] ’09
40](https://image.slidesharecdn.com/yamada-121226022920-phpapp02/85/Coreset-SVM-40-320.jpg)
