Capacitors
- 1. Capacitors Qafqaz Univeristeti: Fizika muÉllimliyi(eng): SÉid ąĘēđÅēđēâąðąđ
- 2. What is capacitor?????? Anyone can say??? Yes we are listening to youâĶ
- 3. Capacitors âĒ Capacitors have many applications: â Computer RAM memory and keyboards. â Electronic flashes for cameras. â Electric power surge protectors. â Radios and electronic circuits.
- 4. Electronic Components ïĩ Capacitors are electronic components that store charge efficiently ïĩ They can be charged and discharged very quickly and hold their charge indefinitely ïĩ Symbol
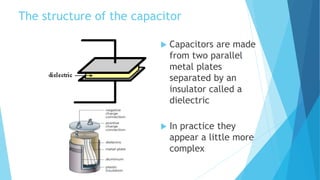
- 5. The structure of the capacitor ïĩ Capacitors are made from two parallel metal plates separated by an insulator called a dielectric ïĩ In practice they appear a little more complex
- 6. Capacitors and Capacitance Charge Q stored: CVQ ï― The stored charge Q is proportional to the potential difference V between the plates. The capacitance C is the constant of proportionality, measured in Farads. Farad = Coulomb / Volt A capacitor in a simple electric circuit.
- 7. Capacitance (symbol C) ïĩ Capacitance is the amount of charge a capacitor can store when connected across a potential difference of 1V (the larger the capacitance the more charge it can store) ïĩ Units of capacitance are Farads (symbol F) ïĩ 1 Farad = 1 coulomb per volt This is a lot of charge!! ïĩ most capacitors are small; ÂĩF (1 x 10-6 F) nF (1 x 10-9 F) pF (1 x 10-12 F) V Q C ï― Where; C=Capacitance in Farads (F) Q=Charge in Coulombs (C) V=Voltage in Volts(V)
- 8. Exercises 1. Calculate the capacitance of a capacitor that stores 1.5 ïī 10-9C at 7.2V?
- 9. Capacitance (C) Three factors determine capacitance; 1. The area of the plates (CïĩA) 2. The distance separating the plates (C ïĩ ) 3. The properties of the dielectric (Îĩr) so C= constant x d 1 d A
- 10. ïĩ If there is air or a vacuum between the plates the constant is; the absolute permittivity of free space (symbol Îĩ0) (Îĩ0 = 8.84 x 10-12 Fm-1) so; d A C 0ïĨ ï― Capacitor Construction Formula
- 11. ïĩ When an insulator (dielectric) is placed between the plates the capacitance increases ïĩ The dielectric constant (symbol Îĩr) gives the proportion by which the capacitance will increase so; and therefore Note that Îĩr has no units as d A C or ïĨïĨ ï― airrdielectic CC ïīï― ïĨ air dielectric r C C ï―ïĨ Insulator Îĩr Air 1 Polystyrene 2.5 Glass 6.0 Water 80 Capacitor Construction Formula
- 12. 1-PLATE AREA: All other factors being equal, greater plate area gives greater capacitance; less plate area gives less capacitance. 2-PLATE SPACING: All other factors being equal, further plate spacing gives less capacitance; closer plate spacing gives greater capacitance.
- 13. 3-DIELECTRIC MATERIAL: All other factors being equal, greater permittivity of the dielectric gives greater capacitance; less permittivity of the dielectric gives less capacitance.
- 14. Examples 1. Calculate the capacitance of a capacitor with a polystyrene dielectric (Îĩr =2.5), an area of 1.2cm by 3.2m and a plate separation of 8 micrometers. d A C or ïĨïĨ ï― (Îĩ0 = 8.84 x 10-12 Fm-1)
- 16. Capacitors in Parallel V C1 C2 Q C Vïš ï âĒWhen capacitors are joined at both ends like this, they are said to be in parallel âĒThey have the same voltage across them âĒThey can be treated like a single capacitor: 1 1 2 2 Q C V Q C V ï― ï ï― ï 1 2Q Q Qï― ïŦ ïĻ ïĐ1 2C C Vï― ïŦ ï 1 2C C Cï― ïŦ âĒWhen capacitors are joined at one end, with nothing else, they are said to be in series âĒThey have the same voltage across them âĒThey can be treated like a single capacitor: V C 1C 2 1 1 2 2 Q C V Q C V ï― ï ï― ï 1 2 Q Q C C ï― ïŦ1 2V V Vï ï― ï ïŦ ï Q C ï― 1 2 1 1 1 C C C ï― ïŦ Capacitors in Series
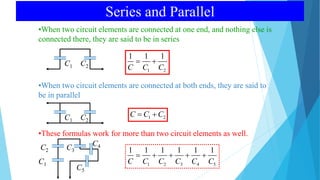
- 17. Series and Parallel âĒWhen two circuit elements are connected at one end, and nothing else is connected there, they are said to be in series 1 2 1 1 1 C C C ï― ïŦ âĒWhen two circuit elements are connected at both ends, they are said to be in parallel 1 2C C Cï― ïŦ C1 C2 C1 C2 âĒThese formulas work for more than two circuit elements as well. C1 C2 C3 C4 C5 1 2 3 4 5 1 1 1 1 1 1 C C C C C C ï― ïŦ ïŦ ïŦ ïŦ
- 18. Examples 1. A circuit has three 330 ΞF capacitors in series. Calculate the total capacitance of the circuit 2. Another circuit has three 330 ΞF capacitors in parallel. Calculate the total capacitance of the circuit.
- 19. âĒ Find the equivalent capacitance seen between terminals a and b of the circuit in Figure.
- 20. Solution: :seriesinarecapacitorsF5andF20 ïï ïïï· F4 520 520 ïï― ïŦ ïī ï F6with theparalleliniscapacitorF4 ïï ïïï· :capacitorsF20and ïï F302064 ïï―ïŦïŦï withseriesiniscapacitorF30 ïïï· capacitor.F60the ïï F20F 6030 6030 ïï ï― ïŦ ïī ï―eqC
- 21. Problems solve at home: 1. A 330ΞF capacitor is charged by a 9.0V battery. How much charge will it store? 2. A 0.1ΞF capacitor stores 1.5 ïī 10-7 C of the charge. What was the voltage used to charge it? 3. Calculate the plate area required for a 1000 ΞF, glass (Îĩr=6.0) capacitor, with a plate separation of 2.8 micrometres. 4. Calculate the dielectic constant of a 10000 ΞF capacitor with a 1.2Ξm plate separation and an area of 16.97m2
- 22. Calculate effective capacitance: a b 15 ΞF 3 ΞF 6 ΞF What is the effective capacitance Cab between points a and b? 20 ΞF C1 C2 C3 C4 Cab ?