![GARIS PASAR SEKURITAS (SML)
Garis pasar sekuritas adalah garis hubungan antara tingkat
return harapan dari suatu sekuritas dengan risiko sistematis
(beta).
SML dapat digunakan untuk menilai keuntungan suatu aset
individual pada kondisi pasar yang seimbang. Sedangkan CML
dapat dipakai untuk menilai tingkat return harapan dari
suatu portofolio yang efisien, pada suatu tingkat risiko
tertentu (sP).
Formula untuk mendapatkan E(R) dari suatu sekuritas
menurut model SML adalah:
dalam hal ini:
[ ]
)
R
(ERM)
R
)
E(R F
i
F
i -
+
= b
M
2
M
i,
i
硫 =](https://image.slidesharecdn.com/capm-240425015414-408d17d5/85/Capital-Asset-Priceng-Model-atau-CAPM-11-15-320.jpg)
![RETURN SEKURITAS YANG
DISYARATKAN
Berdasarkan hubungan tingkat return dengan beta, maka komponen
penyusun required rate of return terdiri dari: tingkat return bebas
risiko dan premi risiko.
Secara matematis, hubungan tersebut dapat digambarkan sebagai:
ki = tingkat risiko aset bebas risiko + premi risiko sekuritas
[ ]
F
M
i
F R
)
E(R
硫
R -
+
=
dalam hal ini:
ki = tingkat return yang disyaratkan investor pada sekuritas i (CAPM)
E(RM) = return portofolio pasar yang diharapkan (lihat IHSG)
bi = koefisien beta sekuritas I (lihat di Bloomberg.com atau yahoo.finance)
RF = tingkat return bebas risiko (dilihat dari BI rate atau SBI)
E(RM) - RF = Risk Premium (tambahan dari return apabila investor mengambil risiko untuk membeli saham](https://image.slidesharecdn.com/capm-240425015414-408d17d5/85/Capital-Asset-Priceng-Model-atau-CAPM-11-17-320.jpg)
![Contoh lain :
Diasumsikan beta saham PT Gudang Garam adalah 0,5
dan tingkat return bebas risiko (Rf) adalah 1,5%.
Tingkat return pasar harapan diasumsikan sebesar 2%.
Dengan demikian, maka tingkat keuntungan yang
disyaratkan investor untuk saham PT Gudang Garam
adalah:
= 0,015 + 0,5 (0,02 0,015)
= 1,75%
[ ]
F
M
i
F
GGRM R
)
E(R
R
k -
+
= 硫
RETURN SEKURITAS YANG
DISYARATKAN](https://image.slidesharecdn.com/capm-240425015414-408d17d5/85/Capital-Asset-Priceng-Model-atau-CAPM-11-23-320.jpg)
Capital Asset Priceng Model atau CAPM 11
- 1. Model CAPM Ardi Gunardi, SE., MSi., CSRA Erik Syawal Alghifari, SE., MM FAKULTAS EKONOMI DAN BISNIS UNIVERSITAS PASUNDAN
- 2. CAKUPAN PEMBAHASAN Overview CAPM (Capital Asset Pricing Model) Portofolio pasar Garis pasar modal Garis pasar sekuritas
- 3. OVERVIEW Model dapat digunakan sebagai alat untuk memahami suatu permasalahan yang kompleks dalam gambaran yang lebih sederhana. Untuk memahami bagaimanakah penentuan risiko yang relevan pada suatu aset, dan bagaimanakah hubungan antara risiko dan return yang diharapkan, diperlukan suatu model keseimbangan, yaitu: Model hubungan risiko-return aset ketika pasar dalam kondisi keseimbangan.
- 4. CAPITAL ASSET PRICING MODEL (CAPM) CAPM adalah model hubungan antara tingkat return harapan dari suatu aset berisiko dengan risiko dari aset tersebut pada kondisi pasar yang seimbang. CAPM dibangun di atas pondasi teori portofolio Markowitz Berdasarkan teori portofolio Markowitz, portofolio yang efisien adalah portofolio yang berada di sepanjang kurva efficient frontier CAPM diperkenalkan secara terpisah oleh Sharpe, Lintner dan Mossin pada pertengahan 1960-an.
- 5. Asumsi-asumsi model CAPM: 1. Investor akan mendiversifikasikan portolionya dan memilih portofolio yang optimal sesuai dengan garis portofolio efisien. 2. Semua investor mempunyai distribusi probabilitas tingkat return masa depan yang identik. 3. Semua investor memiliki periode waktu yang sama. 4. Semua investor dapat meminjam atau meminjamkan uang pada tingkat return yang bebas risiko. 5. Tidak ada biaya transaksi, pajak pendapatan, dan inflasi. 6. Terdapat banyak sekali investor, sehingga tidak ada investor tunggal yang dapat mempengaruhi harga sekuritas. Semua investor adalah price taker. 7. Pasar dalam keadaan seimbang (equilibrium). CAPITAL ASSET PRICING MODEL (CAPM)
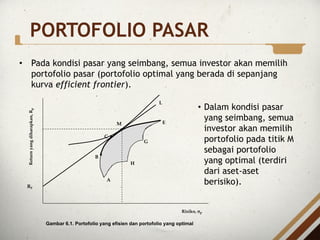
- 6. PORTOFOLIO PASAR Pada kondisi pasar yang seimbang, semua investor akan memilih portofolio pasar (portofolio optimal yang berada di sepanjang kurva efficient frontier). RF L Risiko, sp A E H G M C Return yang diharapkan, R p B Gambar 6.1. Portofolio yang efisien dan portofolio yang optimal Dalam kondisi pasar yang seimbang, semua investor akan memilih portofolio pada titik M sebagai portofolio yang optimal (terdiri dari aset-aset berisiko).
- 7. Portofolio pada titik M (portofolio pasar) akan selalu terdiri dari semua aset berisiko, dan merupakan portofolio aset berisiko yang optimal. Dengan demikian risiko portofolio pasar hanya terdiri dari risiko sistematis (risiko yang tidak dapat dihilangkan oleh diversifikasi). Secara umum, portofolio pasar dapat diproksi dengan nilai indeks pasar, seperti IHSG atau LQ45 untuk kasus di Indonesia. PORTOFOLIO PASAR
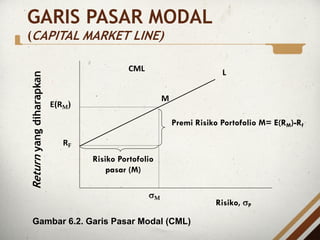
- 8. GARIS PASAR MODAL (CAPITAL MARKET LINE) Garis pasar modal menggambarkan hubungan antara return harapan dengan risiko total dari portofolio efisien pada pasar yang seimbang. Jika kurva efficient frontier pada Gambar 6.1 dihilangkan, dan titik M sebagai portofolio aset berisiko yang optimal diambil, maka kita akan mendapatkan garis Rf-L yang merupakan garis pasar modal (CML), seperti disajikan pada Gambar 6.2.
- 9. Return yang diharapkan L Risiko, sP Risiko Portofolio pasar (M) sM E(RM) M RF CML Premi Risiko Portofolio M= E(RM)-Rf Gambar 6.2. Garis Pasar Modal (CML) GARIS PASAR MODAL (CAPITAL MARKET LINE)
- 10. SLOPE CML Kemiringan (slope) CML menunjukkan harga pasar risiko (market price of risk) untuk portofolio yang efisien atau harga keseimbangan risiko di pasar. Slope CML dapat dihitung dengan: Slope CML mengindikasikan tambahan return yang disyaratkan pasar untuk setiap 1% kenaikan risiko portofolio. CML Slope R - ) E(R M F M =
- 11. Contoh: Dalam kondisi pasar yang seimbang, return yang diharapkan pada portofolio pasar adalah 15% dengan deviasi standar sebesar 20%. Tingkat return bebas risiko sebesar 8%. Maka Slope CML adalah sebesar: Slope CML = (0,15 - 0,08) : 0,20 = 0,35 CML Slope R - ) E(R M F M = SLOPE CML
- 12. PERSAMAAN CML Dengan mengetahui slope CML dan garis intersep (RF), maka kita dapat membentuk persamaan CML menjadi: dalam hal ini: E (Rp) = tingkat return yang diharapkan untuk suatu portofolio yang efisien pada CML RF = tingkat return pada aset yang bebas yang risiko E(RM) = tingkat return portofolio pasar (M) sM = deviasi standar return pada portofolio pasar sP = deviasi standar portofolio efisien yang ditentukan p M F M F P R ) E(R R ) E(R - + =
- 13. PENJELASAN MENGENAI CML 1. Garis pasar modal terdiri dari portofolio efisien yang merupakan kombinasi dari aset berisiko dan aset bebas risiko. Portofolio M, merupakan portofolio yang terdiri dari aset berisiko, atau disebut dengan portofolio pasar. Sedangkan titik RF, merupakan pilihan aset bebas risiko. Kombinasi atau titik-titk portofolio di sepanjang garis RF-M, merupakan portofolio yang efisien bagi investor. 2. Slope CML akan cenderung positip karena adanya asumsi bahwa investor bersifat risk averse. Artinya, investor hanya akan mau berinvestasi pada aset yang berisiko, jika mendapatkan kompensasi berupa return harapan yang lebih tinggi.
- 14. 3. Berdasarkan data historis, adanya risiko akibat perbedaan return aktual dan return harapan, bisa menyebabkan slope CML yang negatif. Slope negatif ini terjadi bila tingkat return aktual portofolio pasar lebih kecil dari tingkat keuntungan bebas risiko. 4. Garis pasar modal dapat digunakan untuk menentukan tingkat return harapan untuk setiap risiko portofolio yang berbeda. PENJELASAN MENGENAI CML
- 15. GARIS PASAR SEKURITAS (SML) Garis pasar sekuritas adalah garis hubungan antara tingkat return harapan dari suatu sekuritas dengan risiko sistematis (beta). SML dapat digunakan untuk menilai keuntungan suatu aset individual pada kondisi pasar yang seimbang. Sedangkan CML dapat dipakai untuk menilai tingkat return harapan dari suatu portofolio yang efisien, pada suatu tingkat risiko tertentu (sP). Formula untuk mendapatkan E(R) dari suatu sekuritas menurut model SML adalah: dalam hal ini: [ ] ) R (ERM) R ) E(R F i F i - + = b M 2 M i, i 硫 =
- 16. Pada Gambar 6.3, risiko sekuritas ditunjukkan oleh beta, yang menunjukkan sensitivitas return sekuritas terhadap perubahan return pasar. Aset yang risikonya lebih kecil dari pasar Risiko (b) 1.5 0.5 0 bM=1 SML A B Return yang diharapkan kM kRF Aset yang risikonya lebih besar dari pasar Gambar 6.3 Garis Pasar Sekuritas (SML) GARIS PASAR SEKURITAS (SML)
- 17. RETURN SEKURITAS YANG DISYARATKAN Berdasarkan hubungan tingkat return dengan beta, maka komponen penyusun required rate of return terdiri dari: tingkat return bebas risiko dan premi risiko. Secara matematis, hubungan tersebut dapat digambarkan sebagai: ki = tingkat risiko aset bebas risiko + premi risiko sekuritas [ ] F M i F R ) E(R 硫 R - + = dalam hal ini: ki = tingkat return yang disyaratkan investor pada sekuritas i (CAPM) E(RM) = return portofolio pasar yang diharapkan (lihat IHSG) bi = koefisien beta sekuritas I (lihat di Bloomberg.com atau yahoo.finance) RF = tingkat return bebas risiko (dilihat dari BI rate atau SBI) E(RM) - RF = Risk Premium (tambahan dari return apabila investor mengambil risiko untuk membeli saham
- 18. Mencari RF = Risk Free Masuk ke : https://www.bi.go.id/id/default.aspx
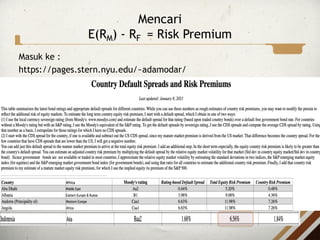
- 19. Mencari bi (beta saham) Masuk ke : https://finance.yahoo.com nanti tinggal cari saham apa yg akan kita analisis misal : PT. Ultra Jaya Milk
- 20. Mencari E(RM) - RF = Risk Premium Masuk ke : https://pages.stern.nyu.edu/~adamodar/
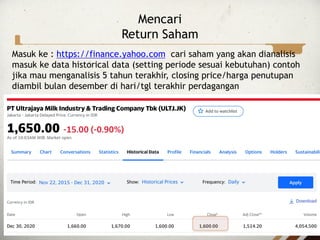
- 21. Mencari Return Saham Masuk ke : https://finance.yahoo.com cari saham yang akan dianalisis masuk ke data historical data (setting periode sesuai kebutuhan) contoh jika mau menganalisis 5 tahun terakhir, closing price/harga penutupan diambil bulan desember di hari/tgl terakhir perdagangan
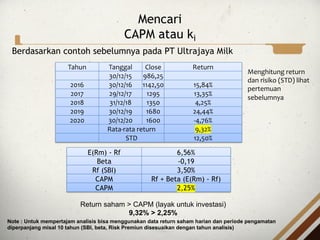
- 22. Mencari CAPM atau ki Berdasarkan contoh sebelumnya pada PT Ultrajaya Milk Tahun Tanggal Close Return 30/12/15 986,25 2016 30/12/16 1142,50 15,84% 2017 29/12/17 1295 13,35% 2018 31/12/18 1350 4,25% 2019 30/12/19 1680 24,44% 2020 30/12/20 1600 -4,76% Rata-rata return 9,32% STD 12,50% E(Rm) - Rf 6,56% Beta -0,19 Rf (SBI) 3,50% CAPM Rf + Beta (E(Rm) - Rf) CAPM 2,25% Return saham > CAPM (layak untuk investasi) 9,32% > 2,25% Note : Untuk mempertajam analisis bisa menggunakan data return saham harian dan periode pengamatan diperpanjang misal 10 tahun (SBI, beta, Risk Premiun disesuaikan dengan tahun analisis) Menghitung return dan risiko (STD) lihat pertemuan sebelumnya
- 23. Contoh lain : Diasumsikan beta saham PT Gudang Garam adalah 0,5 dan tingkat return bebas risiko (Rf) adalah 1,5%. Tingkat return pasar harapan diasumsikan sebesar 2%. Dengan demikian, maka tingkat keuntungan yang disyaratkan investor untuk saham PT Gudang Garam adalah: = 0,015 + 0,5 (0,02 0,015) = 1,75% [ ] F M i F GGRM R ) E(R R k - + = 硫 RETURN SEKURITAS YANG DISYARATKAN
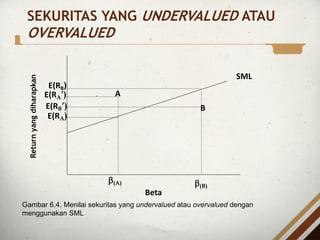
- 24. SEKURITAS YANG UNDERVALUED ATAU OVERVALUED b(B) b(A) E(RB) E(RB) E(RA) E(RA) B A SML Beta Return yang diharapkan Gambar 6.4. Menilai sekuritas yang undervalued atau overvalued dengan menggunakan SML
- 25. Secara teoritis, harga sekuritas seharusnya berada pada SML karena titik-titik pada SML menunjukkan tingkat return harapan pada suatu tingkat risiko sistematis tertentu. Jika tingkat return harapan tidak berada pada SML, maka sekuritas tersebut undervalued atau overvalued. SEKURITAS YANG UNDERVALUED ATAU OVERVALUED
- 26. Pada Gambar 6.4. telihat bahwa sekuritas A terletak di atas SML dan dinilai sebagai sekuritas yang ternilai rendah (undervalued) karena tingkat return harapan E(RA) > retun yang disyaratkan investor E(RA). Sedangkan sekuritas B terletak di bawah SML, sehingga sekuritas B dikatakan ternilai lebih (overvalued). SEKURITAS YANG UNDERVALUED ATAU OVERVALUED
- 27. CONTOH LAIN PENGGUNAAN CAPM 1. Anggap tingkat return bebas risiko adalah 10 persen. Return harapan pasar adalah 18 persen. Jika saham YOY mempunyai beta 0,8, berapakah return disyaratkan berdasarkan CAPM? ki = 10% + 0,8 x (18%-10%) = 16,4% 2. Anggap tingkat return bebas risiko adalah 10 persen. Return harapan pasar adalah 18 persen. Jika saham lain yaitu saham GFG mempunyai return disyaratkan 20 persen, berapakah betanya? 20% = 10% + 硫i x (18%-10%) 10% = 硫i x 8% 硫i = 1,25
- 28. Terima Kasih