Carry look ahead adder
- 2.  Ripple carry adder (RCA)  Drawbacks of RCA  Carry look ahead adder (CLA)  Generalized expression of carry vector  Hardware implementation of CLA © Dr. Prasenjit Dey
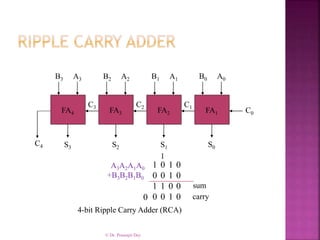
- 3. © Dr. Prasenjit Dey C0 A0B0 S0 A1B1 S1 A2B2 S2 A3B3 S3 C1C2C3 C4 4-bit Ripple Carry Adder (RCA) FA1FA2FA3FA4 A3A2A1A0 +B3B2B1B0 0 0 0 0 1 1 0 1 0 0 1 0 1 0 1 0 sum carry0 1
- 4.  In RCA the carry propagates from the 0th bit position to the nth bit position sequentially  Initially, 1st carry is generated, then from 1st carry, 2nd carry generates and so on.  Now, for nth bit addition we need the (n-1)th carry bit, which generates from the propagation of 0th carry bit(initial carry)  The large the value of n is, the larger the carry propagation time will be  Carry look-ahead (CLA) generates the all carry bits in advance from the input operands only  Thus, reduces carry propagation time  For nth bit addition, it doesn't need to wait for the (n-1)th carry bit to be propagates from the initial carry © Dr. Prasenjit Dey
- 5.  Let us first took at the expression of sum & carry in full adder © Dr. Prasenjit Dey iiiiiii iiii cycxyxc cyxs   1 iiiiii iiii yxPandyxGwhere cPGc  1 )()( iiiiiiiiii xxcyyycxyx  iiiiiiiiiiiiii cyxcyxcyxcyxyx  iiiiiiiiiii cyxcyxcyxyx  )()(1 iiiiiiii cyxyxcyx  iiiiii cyxyxc )(1  iii cps  Pi = ith propagated Carry Gi = ith Generated Carry Gi and Pi are not dependent of ci
- 6. © Dr. Prasenjit Dey iiii cPGc 1 00101212111 ......... cPPPGPPPPGPPGPGc iiiiiiiiiii   111   iiii cPGc )( 1111   iiiiii cPGPGc ))(( 222111   iiiiiiii cPGPGPGc )( 222111   iiiiiiiii cPGPPGPGc 2212111   iiiiiiiiiii cPPPGPPGPGc Putting the value of ci in (1) (1) Putting the value of ci-2 Generalized expression for Ci+1
- 7. Carry Vector = [c4, c3, c2, c1, c0] c0 = cin c1 = c0p0 + g0 c2 = c1p1 + g1 = c0p0p1 + g0p1 + g1 c3=c2p2 + g2 = c0p0p1p2+g0p1p2+g1p2 + g2 c4 = c3p3 + g3= c0P0p1p2p3+g0p1p2p3+g1p2p3+g2p3 + g3 © Dr. Prasenjit Dey
- 8.  When we already have A, B, Cin, we can get all the carries by 3 gate delays  1 gate delay for getting Pi and Gi  2 gate delays in the AND-OR circuit for ci+1  After getting all the carries, we can obtain the sum in 1 gate delay  In ideal scenario, n-bit addition requires (3+1)=4 gate delays © Dr. Prasenjit Dey
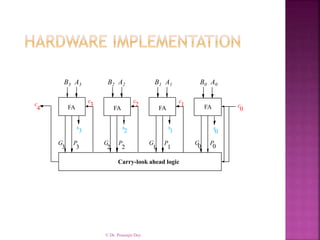
- 9. © Dr. Prasenjit Dey Carry-look ahead logic FA s 3 P 3 G 3 c 3 P 2 G 2 c 2 s 2 G 1 c 1 P 1 s 1 G 0 c 0 P 0 s 0 c 4 B0 FA FA FA A0B1 A1B2 A2B3 A3






![Carry Vector = [c4, c3, c2, c1, c0]
c0 = cin
c1 = c0p0 + g0
c2 = c1p1 + g1 = c0p0p1 + g0p1 + g1
c3=c2p2 + g2 = c0p0p1p2+g0p1p2+g1p2 + g2
c4 = c3p3 + g3= c0P0p1p2p3+g0p1p2p3+g1p2p3+g2p3 + g3
© Dr. Prasenjit Dey](https://image.slidesharecdn.com/carrylookaheadadder-210111171224/85/Carry-look-ahead-adder-7-320.jpg)