Casual learning machine learning with_excel_no2
- 1. カジュアル勉強会 @仙台 Excelで機械学習入門 第2回 株式会社 エクテック 取締役 兼データサイエンティスト
- 3. 前段
- 8. Excel 2013, 2016 Google Spreadsheets
- 9. 本日のアジェンダ 1. 最适化计算の基本となる勾配降下法 2. ラグランジュの缓和法と双対问题 3. モンテカルロ法の基本
- 10. 最适化计算の基本となる勾配降下法
- 11. 前回の话で...
- 14. 少し、脱线します
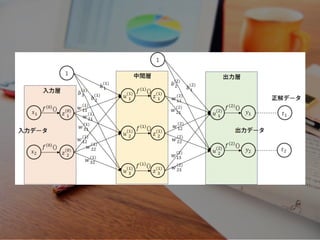
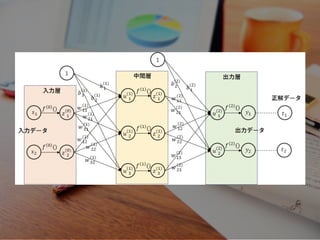
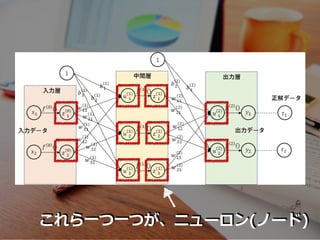
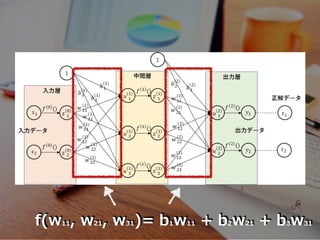
- 17. ニューラルネットワーク
- 20. 『?の脳を模し』た
- 23. f(w11, w21, w31)= b1w11 + b2w21 + b3w31
- 25. 简略化して描いてますが
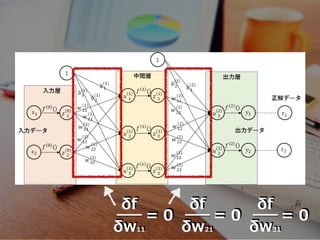
- 29. 勾配降下法 (最急降下法)
- 30. 勾配 = 微分
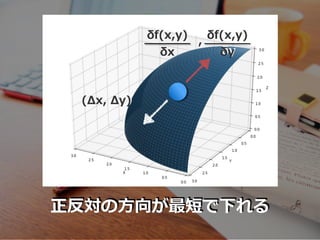
- 31. δf(x,y) δx = 0, δf(x,y) δy = 0 2変数以上 = 偏微分
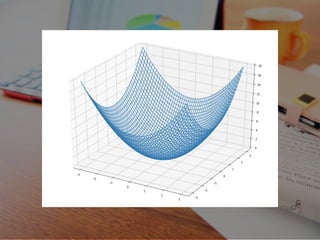
- 32. 2変数について
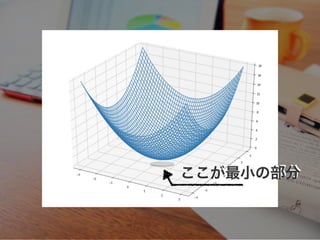
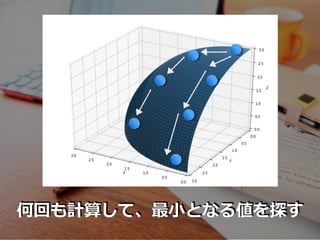
- 34. ここが最小の部分
- 37. いずれ最?のところに?き着く
- 38. これらを公式化してみます
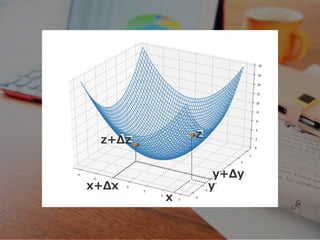
- 40. Δz = f(x+Δx, y+Δy) - f(x, y) 変化 Δzは
- 41. Δz = f(x+Δx, y+Δy) - f(x, y) 変化 Δzは f(x+Δx, y+Δy) = f(x, y) + δf(x,y) δy Δy δf(x,y) δx Δx + ※近似の公式 Δz = δf(x,y) δx Δx + δf(x,y) δy Δy
- 42. これを内积の形で表现すると
- 45. 勾配降下法の基本式
- 46. η (イータ, eta)は ステップサイズ, ステップ幅と呼ばれます δf(x,y) δx , δf(x,y) δy (Δx, Δy) = - η (ただし, ηは正の定数)
- 47. マイナスη これが意味するのは
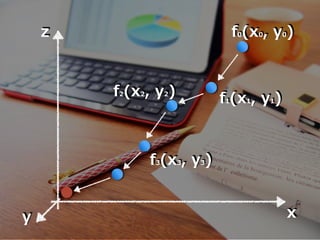
- 49. x z f0(x0, y0) y f1(x1, y1)f2(x2, y2) f3(x3, y3)
- 50. x z f0(x0, y0) y f1(x1, y1)f2(x2, y2) f3(x3, y3) 繰り返し計算していく
- 51. 3変数以上について
- 52. δf δx1 , δf δxn (Δx1, Δx2, …, Δxn) = - η ( δf δx2 , … , )
- 53. δf δx1 , δf δxn (Δx1, Δx2, …, Δxn) = - η ( δf δx2 , … , ) 関数fの点(x1, x2, … , xn)における 勾配
- 54. ηと勾配降下法の注意点
- 55. ηが?きすぎると
- 56. ηが?さすぎると
- 57. 明确な、确実な?法はない
- 58. 地道に 試?錯誤で?つけ出す
- 59. ラグランジュの缓和法と双対问题
- 64. x, yは次の不等式を満たすとき - x - y + 2 ≦ 0, x - y + 2 ≦ 0 下記の関数を最?化する x, y を考える 1 2 (x + y ) 2 2
- 65. 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2 0以上の任意の定数 λ, μを?意すれば と置くことができる
- 67. ここからさらに
- 68. 最?となる m(λ, μ) を?意
- 69. 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 m(λ, μ) ≦
- 70. なおかつ m(λ, μ)が 『最?』となる値 m0 を?意すると
- 71. m(λ, μ) ≦ m0 ≦ 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2
- 72. この λ, μ が得られれば 『x + y を最?化するx, yの値』 が得られる 2 2
- 74. ラグランジュ双体
- 76. ラグランジュ緩和法の左辺 = 1 2 {x - (λ - μ)} + 2 1 2 {y - (λ + μ)} 2 1 2 {(λ - μ) + (λ +μ) } + 2(λ + μ)- 2 2 = 1 2 {x - (λ - μ)} + 2 1 2 {y - (λ + μ)} 2 + 2(λ + μ) - (λ + μ ) 2 2
- 77. よって、x,y が x = λ - μ, y = λ + μ のとき 最?値となる
- 78. よって、x,y が x = λ - μ, y = λ + μ のとき 最?値となり、元々の不等式 - x - y + 2 ≦ 0, x - y + 2 ≦ 0 に代?して整理すると λ ≧ 1, μ ≧ 1
- 79. ??、最?値 m(λ, μ)は m(λ, μ) = 2(λ + μ) - (λ + μ ) = 2 - (λ - 1) + (μ - 1) 2 2 2 2
- 80. λ ≧ 1, μ ≧ 1 と合わせて 最?値m0 は m0 = 2 (λ = 1, μ = 1)
- 81. このとき、x, y は x=0, y=2 そして、x + y の最?値は 2 2 2
- 82. モンテカルロ法の基本
- 86. 第2回は、 以上となります
- 88. EoF