Casual learning machine learning with_excel_no3
- 1. カジュアル勉強会 @仙台 Excelで機械学習入門 第3回 株式会社 エクテック データサイエンティスト
- 3. 前段
- 8. Excel 2013, 2016 Google Spreadsheets
- 10. 前回のやり残し
- 11. 『数式ばかりで、わかりづらい』
- 12. m(λ, μ) ≦ m0 ≦ 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2
- 13. これの意味するものは...
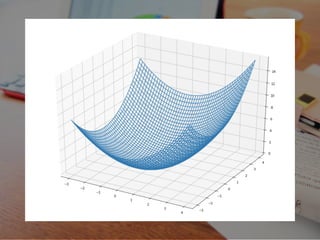
- 14. m(λ, μ) ≦ m0 ≦ 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2
- 16. m(λ, μ) ≦ m0 ≦ 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2
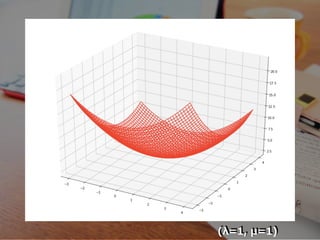
- 17. (λ=1, μ=1)
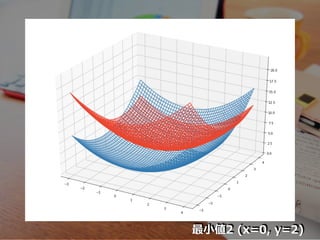
- 18. m(λ, μ) ≦ m0 ≦ 1 2 (x + y ) + λ(-x-y+2) + μ(x-y+2) 2 2 ≦ 1 2 (x + y ) 2 2
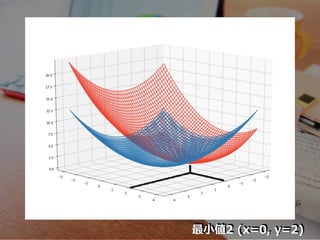
- 19. 最?値2 (x=0, y=2)
- 20. 最?値2 (x=0, y=2)
- 21. 遗伝的アルゴリズム
- 22. ηと勾配降下法の注意点
- 23. ηが?きすぎると
- 24. ηが?さすぎると
- 25. 明确な、确実な?法はない
- 26. 地道に 試?錯誤で?つけ出す
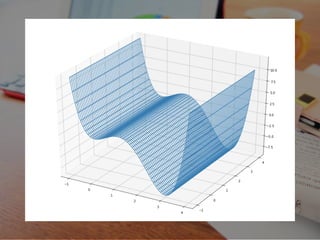
- 32. 16 3 x 3 f(x) = x - 4 + 6x 2 この関数の、最?値とそのときの x を求めたいとします
- 34. 極?値 最?値
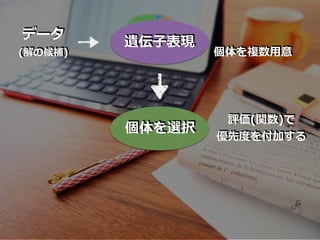
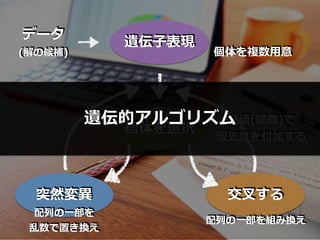
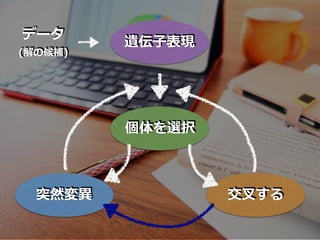
- 37. 遗伝的アルゴリズムとは?
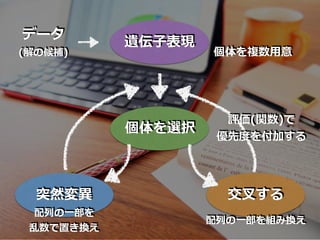
- 38. 『選択』『交叉』 『突然変异』
- 44. 16 3 x 3 f(x) = x - 4 + 6x 2 この関数の、最?値とそのときの x を求めたいとします
- 45. 遗伝?表现
- 46. ランダムに、x を選択する 7, 9, 12, 13
- 47. ランダムに、x を選択する 7, 9, 12, 13 “0111”, “1001”, “1100”, “1101” 2進数表記して「個体」とします
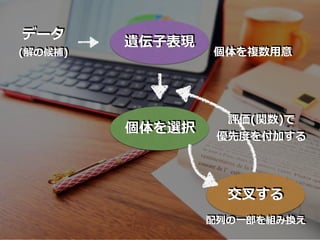
- 48. 个体を选択
- 49. これらが、どれほど環境(関数f(x)) に適しているか f(0111) = 865.7 f(1001) = 3159.0 f(1100) = 12384.0 f(1101) = 17857.7
- 51. これらが、どれほど環境(関数f(x)) に適しているか f(0111) = 865.7 f(1001) = 3159.0 f(1100) = 12384.0 f(1101) = 17857.7
- 52. ”0111”, “1001”
- 54. 交叉する
- 57. 01 | 11 10 | 01 01 | 01 10 | 11 (親) (?) 交叉
- 58. “0111”, “1001”, “1100”, “1101” (現世代) “0111”, “1001”, “0101”, “1011” (次世代)
- 59. 突然変异
- 64. ベイズの定理
- 65. ベイズ理论?ベイズ推论
- 67. 出発点は、「ベイズの定理」
- 68. 条件付き确率
- 69. ?本?の成?男?の割合は順に 49%, 51%です。 また、喫煙率は男性が 28%, ?性が 9%です。 成??本?から無作為に1?を抽出したとき、 男性である事象を M, ?性である事象を F、 喫煙者である事象を Sとします。 (2018年総務省統計局及びJT調査)
- 70. 成??本?の全体(P) M 49% F 51% M 28% F 9% S P(M) = 0.49, P(F) = 0.51, P(S|M) = 0.28, P(S|F) = 0.09
- 72. 乗法定理 P(A∩B) = P(A)P(B|A) P(A∩B) 事象A, Bが同時に起こる確率 P(B|A) 条件付き确率
- 73. P(M) = 0.49, P(F) = 0.51, P(S|M) = 0.28, P(S|F) = 0.09 P(S∩M) = P(M∩S) = P(M)P(S|M) =0.49 ? 0.28 = 0.14, P(S∩F) = P(F∩S) = P(F)P(S|F) =0.51 ? 0.09 = 0.046, P(S) = P(S∩M) + P(S∩F) =0.14 + 0.046 = 0.186
- 76. 乗法定理 P(A∩B) = P(A)P(B|A) P(A∩B) 事象A, Bが同時に起こる確率 P(B|A) 条件付き确率 2つの事象A, Bについて 次の式が成?します
- 77. P(A∩B) = P(A)P(B|A) P(B∩A) = P(B)P(A|B) A∩B A∩B B A B A P(B∩A) = P(B)P(A|B)P(A∩B) = P(A)P(B|A)
- 78. P(A∩B) = P(B∩A)なので P(B)P(A|B) = P(A)P(B|A) P(B) ≠ 0を仮定すれば P(B|A)P(A) P(B) P(A|B) = 証明終
- 84. P(D|H)P(H) P(D) P(M|S) = P(S) = P(D) = 0.18, P(S|M)P(M) = P(D|H)P(H) = 0.14 0.14 0.18 P(M|S) = = 0.78
- 85. 原因の确率
- 87. H D P(D|H) 仮定(原因) 結果(データ) D H P(H|D) 結果(データ) 仮定(原因) ベイズの定理 結果であるデータから、 ”原因の确率”を得ることができる(ベイズ推論)
- 88. 现実问题に、即していきます
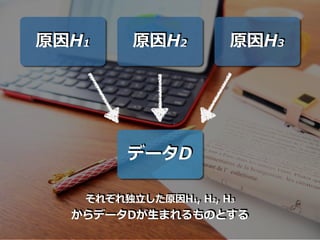
- 89. 原因H1 原因H2 原因H3 データD それぞれ独?した原因H1, H2, H3 からデータDが?まれるものとする
- 90. D H1 H2 H3 D∩H1 D∩H2 D∩H3 P(D) = P(D∩H1) + P(D∩H2) + P(D∩H3)
- 91. P(D) = P(D∩H1) + P(D∩H2) + P(D∩H3) P(D) = P(D|H1)P(H1) + P(D|H2)P(H2) + P(D|H3)P(H3) ※乗法定理 P(A∩B) = P(A)P(B|A)
- 92. P(D) = P(D|H1)P(H1) + P(D|H2)P(H2) + P(D|H3)P(H3) P(D|H1)P(H1) P(D) P(H1|D) = ベイスの定理を使って、原因H1に注?してみる = P(D|H1)P(H1) P(D|H1)P(H1) + P(D|H2)P(H2) + P(D|H3)P(H3)
- 93. P(D|H1)P(H1) P(D|H1)P(H1) + P(D|H2)P(H2) + P(D|H3)P(H3) データD の原因として3つ考えた場合の、 “原因H1の確率”を表現している
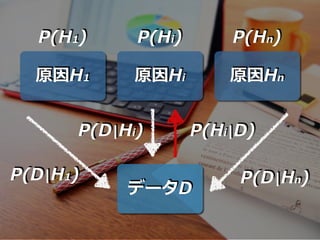
- 94. ?般化して、データDがあり、 原因が {H1, H2, …, Hn}のn個あるとすれば、 データDが得られたとき、その原因が Hiである 確率は下記のように表現できる P(Hi|D) = P(D|Hi)P(Hi) P(D|H1)P(H1) + P(D|H2)P(H2) + … + P(D|Hn)P(Hn) 周辺尤度
- 95. 原因H1 原因Hi 原因Hn データD P(H1) P(Hi) P(Hn) P(Hi|D)P(D|Hi) P(D|H1) P(D|Hn)
- 96. 原因H1 原因Hi 原因Hn データD P(H1) P(D|H1) P(Hn) P(D|Hn) P(Hi) P(D|Hi) P(Hi|D) 事前確率 尤度 事後確率
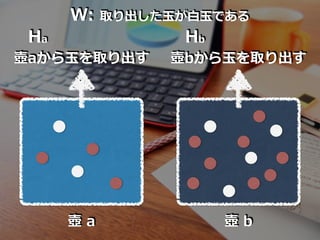
- 97. 壶の问题
- 98. 外からは区別のつかない2つの壺 a, bがあります。 壺 aには??が2個、??が3個、 壺 bには??が4個、??が8個?っています。 いま、壺 a, b のいずれか1つがあり、その壺から ?1個を取り出したら、??だったと?います。 このとき、その壺が aである確率を求めましょう。 また bである確率も求めましょう。
- 99. 壺 a 壺 b Ha Hb 壺aから?を取り出す 壺bから?を取り出す W: 取り出した?が??である
- 101. ベイズの定理から P(W|Ha)P(Ha) P(W|Ha)P(Ha) + P(W|Hb)P(Hb) P(Ha|W) = P(W|Hb)P(Hb) P(W|Ha)P(Ha) + P(W|Hb)P(Hb) P(Hb|W) =
- 102. 尤度 P(W|Ha), P(W|Hb) P(W|Ha) = 「壺aから取り出された?が?であ る確率」 = 2 / (2 + 3) = 2 / 5 P(W|Hb) = 「壺bから取り出された?が?であ る確率」 = 4 / (4 + 8) = 1 / 3
- 103. 事前確率 P(Ha), P(Hb) 問題?の中には、壺a, 壺bがどのような 割合で選ばれるかの情報はない 『等確率』として考えてみる (理由不?分の原則) P(Ha) = P(Hb) = 1/2
- 104. 2/5 ? 1/2 2/5 ? 1/2 + 1/3 ? 1/2 P(Ha|W) = 1/3 ? 1/2 2/5 ? 1/2 + 1/3 ? 1/2 P(Hb|W) = 以上の値を代?すればOK = 6/11 = 5/11
- 107. EoF