�ݺ�ߣ

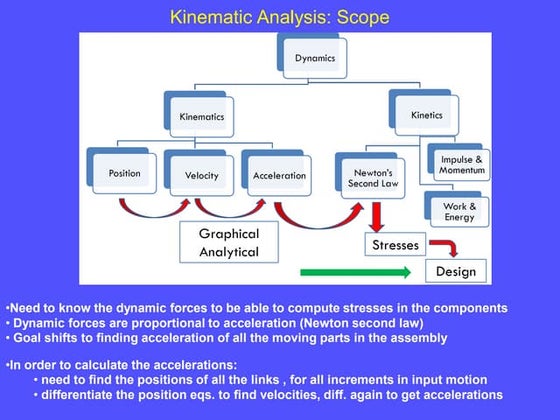
Introduction
Dynamics
Kinematics
Position Velocity Acceleration
Kinetics
Newton’s
Second Law
Work &
Energy
Impulse &
Momentum
Stresses
Design
Graphical
Analytical

Coordinate Systems
 Global or Absolute
 Attached to Earth
 Local
 Attached to a link at some point
of interest
 LNCS (local nonrotating
coordinate system)
 LRCS (local rotating coordinate
system)

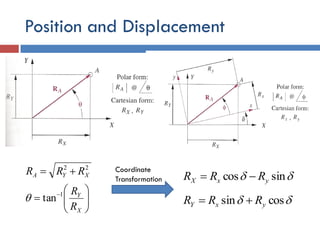
Position and Displacement
22
XYA RRR 






 
X
Y
R
R1
tan
Coordinate
Transformation  sincos yxX RRR 
 cossin yxY RRR 

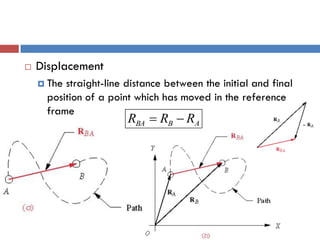
 Displacement
 The straight-line distance between the initial and final
position of a point which has moved in the reference
frame
ABBA RRR 

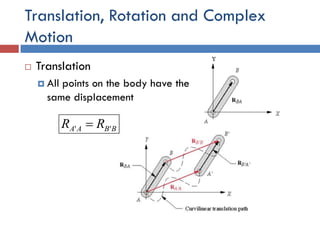
Translation, Rotation and Complex
Motion
 Translation
 All points on the body have the
same displacement
BBAA RR '' 

Motion
 Rotation
 Different points in the body
undergo different
displacements and thus there is
a displacement difference
between any two points chosen
 Euler’s theorem
BAABBB RRR  ''

Motion
 Complex Motion
 Is the sum of the translation and
rotation
 Chasles’Theorem
'"'" BBBBBB RRR 
'"'" ABAAAB RRR 

Graphical Position Analysis
 For any one-DOF, such a fourbar, only one
parameter is needed to completely define the
positions of all the links. The parameter usually
chosen is the angle of the input link.

 Construction of the graphical solution
 The a, b, c, d and the angle θ2 of the input link are
given.
 1. The ground link (1) and the input link (2) are
drawn to a convenient scale such that they
intersect at the origin O2 of the global XY
coordinate system with link 2 placed at the input
angle θ2.
 2. Link 1 is drawn along the X axis for
convenience.

 3. The compass is set to the scaled length of link
3, and an arc of that radius swung about the end
of link 2 (point A).

 4. Set the compass to the scaled length of link 4,
and a second arc swung about the end of link 1
(point O4). These two arcs will have two
intersections at B and B’ that define the two
solution to the position problem for a fourbar
linkage which can be assembled in two
configurations, called circuits, labeled open and
crossed.
 5. The angles of links 3 and 4 can be measured
with a protractor.

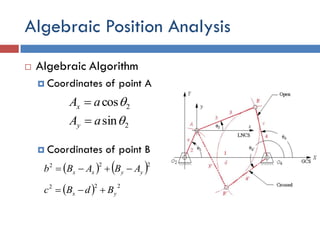
Algebraic Position Analysis
 Algebraic Algorithm
 Coordinates of point A
 Coordinates of point B
2cosaAx 
2sinaAy 
   222
yyxx ABABb 
  222
yx BdBc 

 Coordinates of point B
     dA
BA
S
dA
BA
dA
dcba
B
x
yy
x
yy
x
x







2
2
2
2
2
2222
02
2
2







 c
dA
BA
SB
x
yy
y
P
PRQQ
By
2
42


 
12
2



dA
A
P
x
y
 
dA
SdA
Q
x
y



2
  22
cSdR 
 dA
dcba
S
x 


2
2222

 Link angles for the
given position








 
xx
yy
AB
AB1
3 tan







 
dB
B
x
y1
4 tan

 Vector Loop
 Links are represented as position vectors

 Complex Numbers as Vector
 Unit vectors

 Complex number notation

 Euler identity

sincos je j




j
j
je
d
de



 Vector Loop Equation
for a Fourbar Linkage
 Position vector
 Complex number
notation
01432  RRRR

01432
  jjjj
decebeae
0Independent
variable
To be
determine

 Vector Loop Equation for a
Fourbar Linkage
 Euler equivalents and separate
into two scalar equations
 
 24
23
,,,,
,,,,


dcbaf
dcbaf


        0sincossincossincossincos 11443322   jdjcjbja
Real part: 0coscoscos 432  dcba 
0sinsinsin 432   cbaImaginary part:

 Solve simultaneously
 Square and add
dcab  423 coscoscos 
423 sinsinsin  cab 
     2
42
2
423
2
3
22
coscossinsincossin dcacab  
   2
42
2
42
2
coscossinsin dcacab  
 424242
2222
coscossinsin2cos2cos2   accdaddcab

 To simplify, constants are define in terms of the
constant link length,
 Substituting the identity,
 Freudenstein’s equation
a
d
K 1
424232241 sinsincoscoscoscos   KKK
c
d
K 2
ac
dcba
K
2
2222
3


  424242 sinsincoscoscos  
 4232241 coscoscos   KKK

 Using half angle identities,
 Simplified form














2
tan1
2
tan2
sin
42
4
4


















2
tan1
2
tan1
cos
42
42
4



0
2
tan
2
tan 442












CBA

  3221
2
32212
cos1
sin2
coscos
KKKC
B
KKKA







 The solution,
 If the solution is complex conjugate, the link lengths
chosen are not capable of connection
 The solution will usually be real and unequal
 Crossed (+)
 Open (-)
A
ACBB
2
4
2
tan
2
4 













 

A
ACBB
2
4
arctan2
2
4 2,1


 Solution for θ3
 Square and add
dbac  324 coscoscos 
324 sinsinsin  bac 
323252431 sinsincoscoscoscos   KKK
b
d
K 4
ab
badc
K
2
2222
5


0
2
tan
2
tan 332












FED

  5241
2
52412
cos1
sin2
coscos
KKKF
E
KKKD







 The solution,
 If the solution is complex conjugate, the link lengths
chosen are not capable of connection
 The solution will usually be real and unequal
 Crossed (+)
 Open (-)







 

D
DFEE
2
4
arctan2
2
3 2,1


 Fourbar �ݺ�ߣr-Crank
Linkage
 Position vector
 Complex number
notation
01432  RRRR

01432
  jjjj
decebeae
0Independent
variable
To be
determine

 Vector Loop Equation for a
Fourbar Linkage
 Euler equivalents and separate
into two scalar equations
        0sincossincossincossincos 11443322   jdjcjbja
Real part: 0coscoscos 432  dcba 
0sinsinsin 432   cbaImaginary part:

 The solution,
32
2
3
coscos
sin
arcsin1



bad
b
ca






 



 




 

b
ca 2
3
sin
arcsin2

 Inverted �ݺ�ߣr-Crank (p193-p194)

 Geared Fivebar Linkage
 Position vector
015432  RRRRR

015432
  jjjjj
fedecebeae

 Using the relationship
between the two geared
links;
  25
 
012432
   jjjjj
fedecebeae
ratiogear,
anglephase,

 Solution (pag. 196)







 

D
DFEE
2
4
arctan2
2
4 2,1

  
  
   
 









22
22
2
22222
22
22
sinsin2
coscos2
cos2
sinsin2
coscos2
ad
fad
affdcbaC
adcB
fadcA
CAF
BE
ACD



2

 Solution (pag. 196)







 

L
LNMM
2
4
arctan2
2
3 2,1

  
  
   
 









22
22
2
22222
22
22
sinsin2
coscos2
cos2
sinsin2
coscos2
ad
fad
affdcbaK
dabH
fdabG
KGN
HM
GKL



2

 Sixbar Linkage

�ݺ�ߣ

Ch04 position analysis

More Related Content

Ch04 position analysis