chapter 11 structural svm
?
2 likes?2,720 views
機械学習プロフェッショナルシリーズ サポートベクトルマシンの輪講の資料．Chapter 11 構造化SVM．
![Structural SVM (SSVM)の概要
ü?出力?が構造を持つ場合のSVM
§? 多クラスSVMの拡張と考えると理解しやすい
ü?応用例
§? NLPにおける構文木予測[Yue et al. 2007]
§? Bioinformaticsにおけるタンパク質の構造予測[Yu et al.
2006]
ü?出力空間が膨大なので最適化が難しい
§? 切除平面法 (cutting plane training)
この木構造が出力?](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-2-320.jpg)
![実装など
ü?[John Yu et al. 2009]のSSVMの実装のソースコード
が以下で公開されている
§? http://www.cs.cornell.edu/ cnyu/latentssvm/
§? written in C
§? Cornell Univ.のProf. Thorsten の研究グループが沢山論文
を出してるっぽい http://www.cs.cornell.edu/People/tj/
This is an implementation of latent structural SVM accompanying the
ICML '09 paper "Learning Latent Structural SVMs with Latent
Variables". It was developed under Linux and compiles under gcc, built
upon the SVM^light software by Thorsten Joachims. There are two
versions available. The standalone version using the SVM^light QP
solver is available below. Another version using the Mosek quadratic
program solver is also available. It has been developed and tested for a
longer period of time but requires the separate installation of the
solver.](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-3-320.jpg)
![Optimize SSVM
概要
ü?準備として，単一のスラック変数による最適化問題
を示す
ü?その後，切除平面法（cutting plane training）
を示す
ü?（元論文[Joachims et al. 2009]も割と分かりやすい
ので詳しくはそちらを参照したほうがいいかも？）](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-10-320.jpg)
![Cutting Plane Training
概要
ü?制約条件を一つずつ順番に追加していく最適化法
ü?二次計画問題は変数の数Mに対して?(?J
)
の計算量で解けるので，制約条件が少ない間は高速に解ける
ü?必要な制約条件の個数がデータ点の数?に依存しないことが
証明されている[Joachims et al. 2009]](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-14-320.jpg)
![Loss functions
概要
ü?SSVMでは通常のhinge lossでは不十分な場合が多い
§? For example, in natural language parsing, a parse tree that is almost
correct and differs from the correct parse in only one or a few
nodes should be treated differently from a parse tree that is
completely different. [Tsochantaridis et al. 2005]
ü?margin-rescaling, slack-rescalingという２つの方法
でloss functionを導入できる
ü?本にはあまり詳しく書いていないので
[Tsochantaridis et al. 2005] を参照するほうが良い
かも](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-17-320.jpg)
![Application: learning to rank
ü?この損失関数と特徴ベクトルを用いて最適化が可能
ü?ただし，最も違反している制約を高速に見つける必要
がある[Yue et al. 2007]](https://image.slidesharecdn.com/svm11structuralsvm-150912044852-lva1-app6891/85/chapter-11-structural-svm-23-320.jpg)
chapter 11 structural svm
- 1. SVM本読み会 Chapter11. Structural SVM Waseda Univ. Hamada Lab. Taikai Takeda Twitter: @bigsea_t
- 2. Structural SVM (SSVM)の概要 ü?出力?が構造を持つ場合のSVM §? 多クラスSVMの拡張と考えると理解しやすい ü?応用例 §? NLPにおける構文木予測[Yue et al. 2007] §? Bioinformaticsにおけるタンパク質の構造予測[Yu et al. 2006] ü?出力空間が膨大なので最適化が難しい §? 切除平面法 (cutting plane training) この木構造が出力?
- 3. 実装など ü?[John Yu et al. 2009]のSSVMの実装のソースコード が以下で公開されている §? http://www.cs.cornell.edu/ cnyu/latentssvm/ §? written in C §? Cornell Univ.のProf. Thorsten の研究グループが沢山論文 を出してるっぽい http://www.cs.cornell.edu/People/tj/ This is an implementation of latent structural SVM accompanying the ICML '09 paper "Learning Latent Structural SVMs with Latent Variables". It was developed under Linux and compiles under gcc, built upon the SVM^light software by Thorsten Joachims. There are two versions available. The standalone version using the SVM^light QP solver is available below. Another version using the Mosek quadratic program solver is also available. It has been developed and tested for a longer period of time but requires the separate installation of the solver.
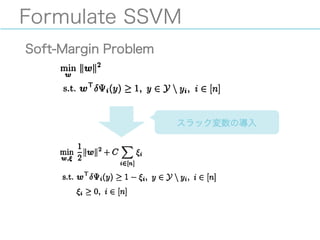
- 4. Formulate SSVM 概要 ü?SSVMの定式化を行う §? 最終的に双対問題を示す ü?分類器は多クラスSVMと同様に，入力xを受け取って 決定関数が最大値を取る出力yを返す関数として定義 される §? ただし，出力が構造yとなっており非常に大きな空間からyを 選択する点で異なる
- 5. Formulate SSVM Notations ü?Decision function ?: ? → ? ? ?, ? = ?+ Ψ(?,?) §? ?: space of input §? Ψ ?, ? : feature vector §? ? ∈ ?0: parameter vector ü?Classifier ?: ? ? → ? ? ?, ? = argmax 9∈? ?(?, ?) §? ?: space of (structural) output
- 8. Formulate SSVM Lagrange Function Dual Problem ?(;9)(<9=) = ?Ψ? y A ?Ψ<(?B) p149の式は誤植
- 10. Optimize SSVM 概要 ü?準備として，単一のスラック変数による最適化問題 を示す ü?その後，切除平面法（cutting plane training） を示す ü?（元論文[Joachims et al. 2009]も割と分かりやすい ので詳しくはそちらを参照したほうがいいかも？）
- 11. 1-Slack Formulation ü?1-slack OP ü?N-slack OP (previous one) 1-slack OP and N-slack OP are equivalent
- 12. 1-Slack Formulation Theorem1. Any solution ?? of 1-slack OP is also a solution of N-slack OP (and vice versa), with ξ? = ∑ ξ? ? ? ?. (prove later) Proof sketch. ü?optimal n-slack ü?optimal 1-slack Therefore, the objective functions are equal for any ?
- 14. Cutting Plane Training 概要 ü?制約条件を一つずつ順番に追加していく最適化法 ü?二次計画問題は変数の数Mに対して?(?J ) の計算量で解けるので，制約条件が少ない間は高速に解ける ü?必要な制約条件の個数がデータ点の数?に依存しないことが 証明されている[Joachims et al. 2009]
- 16. Cutting Plane Training 最も違反をしている制約項の計算 ü??; = ? ? ?;M = 0なので， ü?定数項を無視して， この計算は問題依存
- 17. Loss functions 概要 ü?SSVMでは通常のhinge lossでは不十分な場合が多い §? For example, in natural language parsing, a parse tree that is almost correct and differs from the correct parse in only one or a few nodes should be treated differently from a parse tree that is completely different. [Tsochantaridis et al. 2005] ü?margin-rescaling, slack-rescalingという２つの方法 でloss functionを導入できる ü?本にはあまり詳しく書いていないので [Tsochantaridis et al. 2005] を参照するほうが良い かも
- 18. Loss functions n-slack formulation ü?Margin rescaling ü?Slack rescaling
- 19. Loss functions n-slack formulation ü?Margin rescaling ü?Slack rescaling
- 20. Application: learning to rank 概要 ü?IR（Information Retrieval）への応用 ü?queryに対してコーパス（文書の集合）を関連のある 順（ranking）に並べる問題 relevant ?documents
- 21. Application: learning to rank Evaluation Measure ü?Average Precision(AP) ü?Loss Function
- 22. Application: learning to rank ü?Notations ? = ?Q,… , ? ?|T| ?: ????? ?: ???????? ? ? ??? ?: ? × ? ?;< = _ 1 ? ? ? ? ?; > ?< ?1 ? ? ? ? ?; < ?< 0 ? ? ? ? ?; = ?< ? ?, ? : e. g. ?document ?内のqueryの出現頻度度 ? ?h : ?に関係のある?文書集合 ?h? : ?に関係のない?文書集合 ? 特徴ベクトル
- 23. Application: learning to rank ü?この損失関数と特徴ベクトルを用いて最適化が可能 ü?ただし，最も違反している制約を高速に見つける必要 がある[Yue et al. 2007]
- 24. References ü? 竹内一郎，烏山昌幸， (2015)，サポートベクトルマシン，講談社 ü? Yu, C.-N., Joachims, T., & Elber, R. (2006). Training Protein Threading Models Using Structural SVMs. ICML Workshop on Learning in Structured Output Spaces. ü? Joachims, T., Finley, T., & Yu, C. N. J. (2009). Cutting-plane training of structural SVMs. Machine Learning. doi:10.1007/s10994-009-5108-8 ü? John Yu, C.-N., & Joachims, T. (2009). Learning Structural SVMs with Latent Variables. ü? Tsochantaridis, I., Joachims, T., Hofmann, T., Altun, Y., & Org, A.-C. (2005). Large Margin Methods for Structured and Interdependent Output Variables. Journal of Machine Learning Research, 6, 1453? 1484. ü? Yue, Y., Finley, T., Radlinski, F., & Joachims, T. (2007). A support vector method for optimizing average precision. Proceedings of the 30th annual international ACM SIGIR conference on Research and development in information retrieval , Amsterdam, 271. doi:10.1145/1277741.1277790